For the lower mantle, however, the situation is different as information on the elastic properties of minerals and rocks at pressures and temperatures spanning those of Earth’s lower mantle is more challenging to retrieve, both from experiments and computations. This might be one reason why attempts to interpret the seismic structure of the lower mantle based on incomplete mineral‐physical data have led to contradicting conclusions about the composition and temperature profile of the lower mantle (Cobden et al., 2009; Khan et al., 2008; Matas et al., 2007; Mattern et al., 2005). In recent years, however, important progress has been made in constraining the elastic properties of lower-mantle minerals at high pressures and high temperatures, as for instance by experimental measurements on different bridgmanite compositions (Fu et al., 2018; Kurnosov et al., 2017; Murakami et al., 2012), on unquenchable cubic calcium‐silicate perovskite (Gréaux et al., 2019; Thomson et al., 2019), and on the calcium‐ferrite structured phase (Dai et al., 2013), as well as by better constraining thermoelastic parameters through experiments and computations (Gréaux et al., 2016; Murakami et al., 2012; Yang et al., 2016; Zhang et al., 2013). Similarly, experiments on single crystals (Antonangeli et al., 2011; Crowhurst et al., 2008; Marquardt et al., 2009c, 2009b; Yang et al., 2015), improved computational methods (Wu et al., 2013; Wu and Wentzcovitch, 2014), and measurements at seismic frequencies (Marquardt et al., 2018) have advanced our understanding of how the spin transition of ferrous iron affects the elastic properties of ferropericlase. Many of these and other achievements have not yet been incorporated into mineral‐physical databases, and the effects of spin transitions on mineral elasticity are not accounted for by commonly applied finite‐strain formalisms.
This chapter aims to review recent advancements in experimental and computational mineral physics on the elastic properties of mantle minerals. A brief introduction to finite‐strain theory and to the elastic properties of minerals and rocks is followed by an overview of experimental and computational methods used to determine elastic properties of minerals at pressures and temperatures of Earth’s mantle. To assess the resilience and reliability of mineral‐physical models and their potential to explain seismic observations, I systematically evaluate how uncertainties on individual finite‐strain parameters impact computed elastic wave velocities for major mantle minerals and address the effect of inter‐ and extrapolating elastic properties across complex solid solutions. This analysis aims at revealing the leverages of finite‐strain parameters and extrapolations in chemical compositions on elastic wave velocities in order to guide future efforts to improve mineral‐physical models by reducing uncertainties on key parameters and compositions. With a particular focus on minerals of the lower mantle, I discuss the effect of continuous phase transitions on elastic properties, including ferroelastic phase transitions and spin transitions. A volume-dependent formulation for spin transitions is proposed that is readily combined with existing finite‐strain formalisms. To provide an up‐to‐date perspective on the elastic properties of Earth’s lower mantle, I combine most recent elasticity data and derive elastic wave velocities for a selection of potential mantle rocks, taking into account spin transitions in ferrous and ferric iron and the ferroelastic phase transition in stishovite. A comparison of scenarios for different assumptions about compositional parameters reveals persisting challenges in the mineral physics of the lower mantle.
When a seismic wave passes through a rock, the wave imposes stresses and strains on the rock and on the individual mineral grains that compose the rock. In Earth’s mantle, these stresses and strains are much smaller than those that arise from compression and heating of the rock to pressures and temperatures in the mantle. The mineral grains or crystals react to compression and heating as well as to seismic waves mainly by reversible elastic deformation. For each crystal grain in the rock, the small stresses and strains imposed by a seismic wave can be assumed to obey a linear relationship between the stress tensor σ ijand the infinitesimal strain tensor e ij(Haussühl, 2007; Nye, 1985):
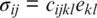
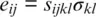
with the components of the elastic stiffness tensor c ijkland the elastic compliance tensor s ijklof the crystal.
Large strains that arise from compression and thermal expansion can be described by the Eulerian finite‐strain tensor E ij(Birch, 1947; Davies, 1974; Stixrude & Lithgow‐Bertelloni, 2005). For hydrostatic compression and heating, the resulting finite strain is dominated by volume strain and can be approximated by an isotropic tensor with E ij= − fδ ijwhere f = [( V 0/ V ) 2/3− 1]/2. V 0/ V is the ratio of the volume V 0of the crystal at the reference state to the volume V in the compressed and hot state. In principle, the definition of the reference state is arbitrary. From an experimental point of view, it is convenient to define the reference state to be the state of the mineral at ambient pressure and temperature, i.e., P 0= 1 × 10 –4GPa and T 0= 298 K. Based on an expansion of the Helmholtz free energy F in finite strain, physical properties, including pressure and elastic stiffnesses, can be described as a function of volume and temperature (Birch, 1947; Davies, 1974; Thomsen, 1972a). Throughout this chapter, I will use the self‐consistent formalism presented by Stixrude and Lithgow‐Bertelloni (2005) that combines finite‐train theory with a quasi‐harmonic Debye model for thermal contributions to calculate pressure and elastic properties (Ita & Stixrude, 1992; Stixrude & Lithgow‐Bertelloni, 2005).
For a truncation of the Helmholtz free energy after the fourth‐order term in finite strain, the components of the isentropic elastic stiffness tensor are given by (Davies, 1974; Stixrude & Lithgow‐Bertelloni, 2005):
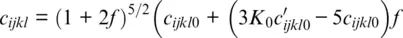
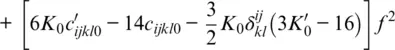
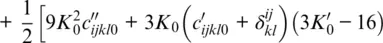
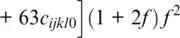
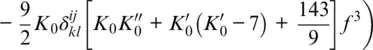
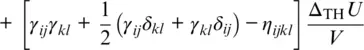
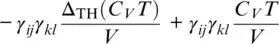
where δijkl = − δ ij δkl − δil δjk − δjl δik . The parameters of the cold part (lines 1–5) of this expression are the components of the isothermal elastic stiffness tensor c ijkl0at the reference state and their first and second pressure derivatives 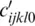 and
and 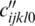 , respectively. They combine to the isothermal bulk modulus K 0at the reference state as:
, respectively. They combine to the isothermal bulk modulus K 0at the reference state as:
Читать дальше

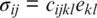
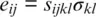
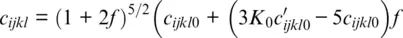
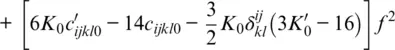
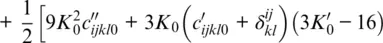
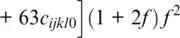
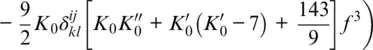
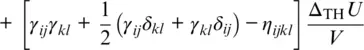
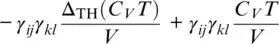
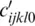 and
and 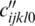 , respectively. They combine to the isothermal bulk modulus K 0at the reference state as:
, respectively. They combine to the isothermal bulk modulus K 0at the reference state as:










