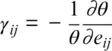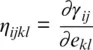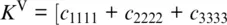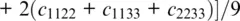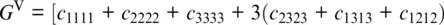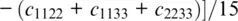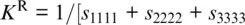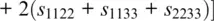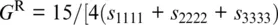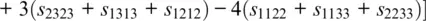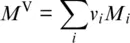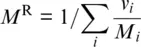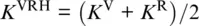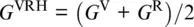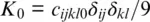
In an analogous way, the first and second pressure derivatives of the components of the elastic stiffness tensor combine to the first and second pressure derivatives of the bulk modulus 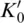 and
and 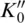 , respectively. The number of independent components of the elastic stiffness tensor depends on the crystal symmetry of the mineral and ranges from 21 for monoclinic (lowest) symmetry to 2 for an elastically isotropic material (Haussühl, 2007; Nye, 1985). Many mantle minerals, including olivine, wadsleyite, and bridgmanite, display orthorhombic crystal symmetry with 9 independent components of the elasticity tensors. For minerals with cubic crystal symmetry, such as ringwoodite, most garnets, and ferropericlase, the number of independent components is reduced to 3.
, respectively. The number of independent components of the elastic stiffness tensor depends on the crystal symmetry of the mineral and ranges from 21 for monoclinic (lowest) symmetry to 2 for an elastically isotropic material (Haussühl, 2007; Nye, 1985). Many mantle minerals, including olivine, wadsleyite, and bridgmanite, display orthorhombic crystal symmetry with 9 independent components of the elasticity tensors. For minerals with cubic crystal symmetry, such as ringwoodite, most garnets, and ferropericlase, the number of independent components is reduced to 3.
The thermal contribution (lines 6–7) includes the changes in internal energy Δ TH U and in the product of isochoric heat capacity C Vand temperature T , Δ TH( C V T ), that result from heating the mineral at constant volume V from the reference temperature T 0to the temperature T . The internal energy U is computed from a Debye model (Ita & Stixrude, 1992) based on an expansion of the Debye temperature θ in finite strain (Stixrude & Lithgow‐Bertelloni, 2005). The Grüneisen tensor is then defined as:
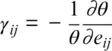
and the strain derivative of the Grüneisen tensor as:
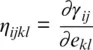
The Grüneisen tensor and the tensor η ijklare functions of finite strain themselves that are parameterized using their values at ambient conditions, i.e., γ ij0and η ijkl0(Stixrude & Lithgow‐Bertelloni, 2005).
Seismic waves travel with wavelengths on the order of kilometers that by far exceed the grain sizes of mantle rocks. Seismic waves thus probe the elastic response of a collection or an aggregate of mineral grains. In the simplest case of a monomineralic aggregate, all grains are crystals of the same mineral. The crystals can be randomly oriented or aligned to form a crystallographic preferred orientation (CPO). CPO can result from deformation or from crystallization of mineral grains under the action of an anisotropic external field (Karato, 2008). In general, crystals are elastically anisotropic, and any preferred orientation of crystals will partly transfer the elastic anisotropy of individual crystals to the aggregate (Mainprice, 2015; Mainprice et al., 2000).
When combining the elastic properties of individual crystals to those of the aggregate, we further have to take into account that stresses and strains may not be distributed homogeneously throughout the aggregate as some crystals may behave stiffer and deform less than others. The effective stiffness of a crystal depends on the orientation of the crystal with respect to the imposed stress and strain fields. Crystals may also be clamped between neighboring grains and be forced into a strain state that may not correspond to a state of unconstrained mechanical equilibrium with the imposed external stress field. Approximations and bounds to the complex elastic behavior of crystalline aggregates have been reviewed by Watt et al. (1976). Here, I adopt the simplest bounding scheme based on the Voigt and Reuss bounds (Reuss, 1929; Voigt, 1928; Watt et al., 1976) and assume a random orientation of crystals.
The Voigt bound is based on the assumption that the strain is homogeneous throughout the aggregate (Reuss, 1929; Watt et al., 1976). Regardless of its orientation, each crystal in the aggregate is deformed according to the external strain field imposed, for example, by a seismic wave. Because the resulting stresses are calculated from the strains using the elastic stiffnesses, we need to average the components of the elastic stiffness tensor c ijklover all orientations. For a monomineralic aggregate, this leads to the following expressions for the isotropic bulk modulus K and the isotropic shear modulus G (Hill, 1952; Watt et al., 1976):
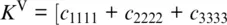
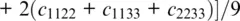
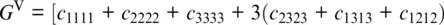
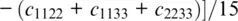
The Reuss bound assumes that the imposed external stress field is homogeneous throughout the aggregate (Reuss, 1929; Watt et al., 1976). In this case, the strains are calculated from the stresses using the components of the elastic compliance tensor s ijkl. The isotropic bulk and shear moduli of a monomineralic aggregate of randomly oriented crystals are then (Hill, 1952; Watt et al., 1976):
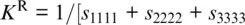
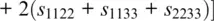
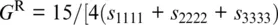
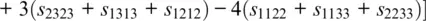
Most mantle rocks are composed of several mineral phases, each of which has different elastic properties. For a polymineralic rock composed of different mineral phases with volume fractions v i, the bulk and shear moduli M iof individual mineral phases are then combined to the Voigt bound as (Watt et al., 1976):
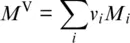
and to the Reuss bound as (Watt et al., 1976):
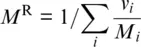
While the Voigt and Reuss averages provide bounds to the elastic behavior of a crystalline aggregate, the Voigt‐Reuss‐Hill averages are often used as an approximation to the actual elastic response (Chung & Buessem, 1967; Hill, 1952; Thomsen, 1972b):
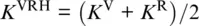
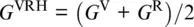
Note that the calculation of the Voigt and Reuss bounds in their strictest sense would require the elastic stiffness and compliance tensors of all minerals in the rock at the respective pressure and temperature. For many minerals, however, bulk and shear moduli have so far only been determined on polycrystalline aggregates and are themselves averages over the elastic properties of many individual crystals. For polycrystalline aggregates, the changes of the aggregate bulk and shear moduli of a mineral that result from compression and heating can be described by combining the finite‐strain expressions for individual components c ijklto finite‐strain expressions for the isotropic bulk and shear moduli (Birch, 1947; Davies, 1974; Stixrude & Lithgow‐Bertelloni, 2005). Under the assumption of isotropic finite strain, the expressions would resemble those for the Voigt bound. In analogy to the elastic moduli, the components of the tensor η ijklare combined to the isotropic parameters η Vand η Swith respect to volume and shear strain, respectively (Stixrude & Lithgow‐Bertelloni, 2005). When determined on a polycrystalline sample, however, aggregate moduli are not readily identified with either of the bounds or with a simple average as the elastic response of the aggregate falls somewhere in between the Voigt and Reuss bounds and may even fall outside the bounds if a CPO is present.
Читать дальше

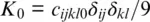
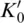 and
and 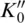 , respectively. The number of independent components of the elastic stiffness tensor depends on the crystal symmetry of the mineral and ranges from 21 for monoclinic (lowest) symmetry to 2 for an elastically isotropic material (Haussühl, 2007; Nye, 1985). Many mantle minerals, including olivine, wadsleyite, and bridgmanite, display orthorhombic crystal symmetry with 9 independent components of the elasticity tensors. For minerals with cubic crystal symmetry, such as ringwoodite, most garnets, and ferropericlase, the number of independent components is reduced to 3.
, respectively. The number of independent components of the elastic stiffness tensor depends on the crystal symmetry of the mineral and ranges from 21 for monoclinic (lowest) symmetry to 2 for an elastically isotropic material (Haussühl, 2007; Nye, 1985). Many mantle minerals, including olivine, wadsleyite, and bridgmanite, display orthorhombic crystal symmetry with 9 independent components of the elasticity tensors. For minerals with cubic crystal symmetry, such as ringwoodite, most garnets, and ferropericlase, the number of independent components is reduced to 3.