For MgSiO 3pPv only two studies report differential stress as a function of pressure (Merkel et al., 2007; Miyagi et al., 2010). A third high‐temperature study reported a differential stress of 0.25–1.5 GPa at a pressure range of 130–156 GPa and 2500–3000 K (Wu et al., 2017), however, in this study the MgSiO 3pPv samples were sandwiched between layers of either NaCl or KCl and so it is likely that the measured stress levels reflect the flow strength of the NaCl or KCl pressure medium rather than that of MgSiO 3pPv.
There is a large pressure gap between the highest‐pressure measurements on Brg at ~60 GPa and strength measurements on MgSiO 3pPv at pressures > 130 GPa ( Figure 2.3). The two measurements on MgSiO 3pPv are similar though those of Merkel et al. (2007) ( Figure 2.3, blue open squares) are higher than those of Miyagi et al. (2010) ( Figure 2.3, green open triangles). For these measurements, Miyagi et al. (2010) used a moment pole stress model and as discussed above the small error bars (smaller than the symbols) only represent fitting errors. In contrast, the study of Merkel et al. (2007) has small errors (smaller than the symbols) but uses the method of Singh et al. (1998). The small error bars in this study are due to that fact that there are only small variations in stresses calculated on different lattice planes.
Differences in differential stress measurements between Miyagi et al. (2010) and Merkel et al. (2007) could be due to composition. A natural enstatite was used for synthesis in Merkel et al. (2007), whereas a synthetic MgSiO 3glass was used as starting material in Miyagi et al. (2010). Another possibility is grain size. Visual comparison of raw diffraction images in these two studies shows spottier diffraction rings in Miyagi et al. (2010), which qualitatively indicates larger grain size, and may result in lower flow strength. Interestingly, if room temperature flow strength measurements on Brg are compared to pPv, the highest value measured in Brg is 11.9 GPa at a pressure of 52 GPa (Miyagi & Wenk, 2016). In pPv the highest differential stress value is 11.1 GPa at 177GPa (Miyagi et al., 2010). If one assumes that pressure increases the flow strength of Brg (as would be expected), then at room temperature pPv may be significantly weaker than Brg. A theoretical study by Ammann et al. (2010) suggests that high‐temperature strength of MgSiO 3pPv may be much lower than Brg based on calculated diffusion coefficients. Likewise, experimental work on pPv analogs found that during high temperature deformation the pPv phase is ~5–10 time weaker than the perovskite (Pv) phase (Dobson et al., 2012; Hunt et al., 2009). If room temperature flow strength is lower and if diffusion is faster in MgSiO 3pPv, there is a high likelihood that Brg is significantly stronger than MgSiO 3pPv over a range of pressure and temperature conditions. If the strength contrast between Brg and pPv is as large as the analog studies indicate then pPv may be similar or even weaker than Fp.
2.4.2 Textures and Slip Systems in Lower Mantle Phases
Recently, Merkel & Cordier (2016) reviewed slip systems in lower mantle and core phases. As such the following discussion will briefly review textures and slip systems in lower mantle phase but will mostly focus on more recent developments. For a more detailed discussion of studies on slip systems prior to 2016 and for a figure showing the relationship between crystal structures and slip systems, the reader is referred to the review by Merkel & Cordier (2016). A summary of experimentally inferred slip systems of lower mantle phases is given in Table 2.1.
Table 2.1 Summary of inferred slip systems in the major lower mantle phases and the conditions under which they are expected to dominate based on experimental data. See text for details of the experiments.
| Mantle phase |
Slip system |
P‐T conditions |
| Ferropericlase |
{110}<1‐0> |
High P, low T |
|
{100}<011> |
High P, high T |
| Ca‐Perovskite |
{110}<1‐10> |
High P low T |
| Bridgmanite |
(001) in [100], [010] or<110> |
P < ~55 GPa, low T |
|
(100)[010] |
P > ~55 GPa, low T |
|
(100){001] |
High P, high T |
| Post‐Perovskite |
(001)[100] |
High P, low T and high P, high T |
|
(010)[100] and (010) |
CalrO 3, high P, low T, and high P, high T |
In compression studies texture development is typically represented by inverse pole figures (IPFs) of the compression direction ( Figures 2.4– 2.5). IPFs show the probability of finding the pole to a lattice plane in the compression direction (i.e., the relationship between one sample direction and all crystallographic plane normals). Texture intensity is typically given in multiples of random distribution (m.r.d.) or multiples of uniform distributions (m.u.d.) where an m.r.d. or an m.u.d. of 1 is random and a higher or lower number represents a greater or fewer number of orientations, respectively. In cases where the deformation geometry is more complex than compression (e.g., simple shear), it common to represent textures with pole figures ( Figure 2.4g). Pole figures show the orientation of a specific lattice plane normal to the sample coordinate system (i.e., one or a few specific lattice planes to all sample directions).
Perhaps due to their stability at ambient conditions Per and Fp are most studied of the mantle phases (Heidelbach et al., 2003; Immoor et al., 2018; F. Lin et al., 2017; Long et al., 2006; Merkel et al., 2002; Stretton et al., 2001; Uchida et al., 2004; Yamazaki & Karato, 2002). For a detailed review of deformation mechanisms in Per the reader is referred to (Amodeo et al., 2018). Slip in Per and Fp occurs in the 〈110〉 direction on {110}, {100} and {111} planes (Amodeo et al., 2018). In both Per and Fp low temperature deformation is by dominant slip on {110}〈1 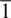 0〉 over a wide range of pressures ( Table 2.1; F. Lin et al., 2017; J.‐F. Lin et al., 2009; Merkel et al., 2002; Paterson & Weaver, 1970; Tommaseo et al., 2006). High pressure compression studies at low temperatures show textures characterized by {100} at high angles to compression which is attributed to slip on {110}〈1
0〉 over a wide range of pressures ( Table 2.1; F. Lin et al., 2017; J.‐F. Lin et al., 2009; Merkel et al., 2002; Paterson & Weaver, 1970; Tommaseo et al., 2006). High pressure compression studies at low temperatures show textures characterized by {100} at high angles to compression which is attributed to slip on {110}〈1 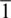 0〉 ( Figure 2.4a, Table 2.1; Immoor et al., 2018; J.‐F. Lin et al., 2009; Marquardt & Miyagi, 2015; Merkel et al., 2002; Tommaseo et al., 2006). High‐temperature studies on Per show increased activity of the {100}〈011〉 slip system with elevated temperature (Appel & Wielke, 1985; Copley & Pask, 1965; Hulse et al., 1963; Paterson & Weaver, 1970; Sato & Sumino, 1980).
0〉 ( Figure 2.4a, Table 2.1; Immoor et al., 2018; J.‐F. Lin et al., 2009; Marquardt & Miyagi, 2015; Merkel et al., 2002; Tommaseo et al., 2006). High‐temperature studies on Per show increased activity of the {100}〈011〉 slip system with elevated temperature (Appel & Wielke, 1985; Copley & Pask, 1965; Hulse et al., 1963; Paterson & Weaver, 1970; Sato & Sumino, 1980).
Theoretical calculations (Amodeo et al., 2012, 2016) and single crystal deformation experiments on Per to 8 GPa (Girard et al., 2012) suggest a possible transition to {100}〈011〉 slip at pressure somewhere between 23 and 40 GPa. High pressure DAC measurement on Fp documented an abrupt increase in yield strength between 20 and 60 GPa, which may be associated with this slip system transition (Marquardt & Miyagi, 2015). However for a transition from {110}〈1  0〉 slip to {100}〈011〉 one would expect a texture change from {100} planes oriented at high angles to compression to {110} planes at high angle to compression ( Figure 2.4a, b). Texture changes associated with a pressure induced slip system changes have not been documented and this may be due to difficulty in overprinting the lower pressure textures (Amodeo et al., 2016).
0〉 slip to {100}〈011〉 one would expect a texture change from {100} planes oriented at high angles to compression to {110} planes at high angle to compression ( Figure 2.4a, b). Texture changes associated with a pressure induced slip system changes have not been documented and this may be due to difficulty in overprinting the lower pressure textures (Amodeo et al., 2016).
Читать дальше

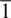 0〉 over a wide range of pressures ( Table 2.1; F. Lin et al., 2017; J.‐F. Lin et al., 2009; Merkel et al., 2002; Paterson & Weaver, 1970; Tommaseo et al., 2006). High pressure compression studies at low temperatures show textures characterized by {100} at high angles to compression which is attributed to slip on {110}〈1
0〉 over a wide range of pressures ( Table 2.1; F. Lin et al., 2017; J.‐F. Lin et al., 2009; Merkel et al., 2002; Paterson & Weaver, 1970; Tommaseo et al., 2006). High pressure compression studies at low temperatures show textures characterized by {100} at high angles to compression which is attributed to slip on {110}〈1 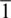 0〉 ( Figure 2.4a, Table 2.1; Immoor et al., 2018; J.‐F. Lin et al., 2009; Marquardt & Miyagi, 2015; Merkel et al., 2002; Tommaseo et al., 2006). High‐temperature studies on Per show increased activity of the {100}〈011〉 slip system with elevated temperature (Appel & Wielke, 1985; Copley & Pask, 1965; Hulse et al., 1963; Paterson & Weaver, 1970; Sato & Sumino, 1980).
0〉 ( Figure 2.4a, Table 2.1; Immoor et al., 2018; J.‐F. Lin et al., 2009; Marquardt & Miyagi, 2015; Merkel et al., 2002; Tommaseo et al., 2006). High‐temperature studies on Per show increased activity of the {100}〈011〉 slip system with elevated temperature (Appel & Wielke, 1985; Copley & Pask, 1965; Hulse et al., 1963; Paterson & Weaver, 1970; Sato & Sumino, 1980). 0〉 slip to {100}〈011〉 one would expect a texture change from {100} planes oriented at high angles to compression to {110} planes at high angle to compression ( Figure 2.4a, b). Texture changes associated with a pressure induced slip system changes have not been documented and this may be due to difficulty in overprinting the lower pressure textures (Amodeo et al., 2016).
0〉 slip to {100}〈011〉 one would expect a texture change from {100} planes oriented at high angles to compression to {110} planes at high angle to compression ( Figure 2.4a, b). Texture changes associated with a pressure induced slip system changes have not been documented and this may be due to difficulty in overprinting the lower pressure textures (Amodeo et al., 2016).










