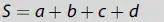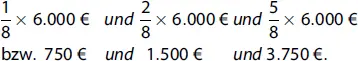Gerhard Janes - Kostenrechnung

k) Einzelkosten sind immer solche Kosten, die einem Produkt unmittelbar direkt zugeordnet werden können.

l) Die Einzelkosten eines Produktes können auch unabhängig von seiner Herstellungs- oder Absatzmenge sein.

m) Bei progressiv variablem Kostenverlauf steigen die Stückkosten mit der Auslastung stetig an.

n) Sprungfixe Kosten steigen bei der Annäherung der Beschäftigung an bestimmte Kapazitätsgrenzen sprunghaft an.

o) Nach dem Identitätsprinzip werden Kosten nur dann einem Produkt zugeordnet, wenn ein Kausalzusammenhang zwischen seiner Herstellung und den Kosten besteht.

p) Die Plankostenrechnung wird oft deswegen eingeführt, weil sie mit geringerem Aufwand als eine Istkostenrechnung verbunden ist.

q) Eine Periodenerfolgsrechnung ermittelt das Betriebsergebnis in Bezug auf die erzeugten Leistungseinheiten.

r) Unechte Gemeinkosten sind Einzelkosten, werden aber wie Gemeinkosten behandelt.

a) Falsch, b) Falsch, c) Richtig, d) Falsch, e) Falsch, f) Richtig, g) Falsch, h) Richtig, i) Richtig, j) Falsch, k) Falsch, l) Richtig, m) Richtig, n) Richtig, o) Falsch, p) Falsch, q) Falsch, r) Richtig.

• Zu a) Richtig ist, dass die Herstellkosten in absoluter Höhe (also die variablen Gesamtkosten) mit der hergestellten Menge ansteigen, die Kosten pro Stück bleiben aber gleich.

• Zu b) Richtig ist, dass in einem ersten Schritt, z. B. bei der Zuordnung der Kosten auf Kostenträger, wie Produkte oder Aufträge, bestimmte (fixe oder indirekte) Kosten unberücksichtigt bleiben. Diese werden allerdings in einem zweiten Schritt in die gesamten Kosten des Unternehmens (z. B. »en bloc«) miteinberechnet.

• Zu d) Richtig wäre der Begriff »Durchschnittskosten« oder »Stückkosten«. Grenzkosten sind die »Kosten des nächsten Stücks«, d. h. die zusätzlichen Kosten, die bei einer zusätzlich erzeugten (oder abgesetzten) Mengeneinheit entstehen.

• Zu e) Sondereinzelkosten des Vertriebes können unabhängig von der hergestellten Menge sein, z. B. ändern sich die Zollkosten für den Export eines Auftrages mehrerer Maschinen nur mit der abgesetzten Menge. Sie können auch unabhängig von der abgesetzten Menge anfallen, wenn z. B. die Transportkosten eines Containers unabhängig davon sind, wieviel Menge in den Container eingefüllt wurde.

• Zu g) Richtig wäre das Tragfähigkeitsprinzip.

• Zu j) Richtig wäre, dass bei Kostenremanenz die Kosten nicht linear mit der Senkung der Produktionsmenge zurückgehen (selbst wenn sie vorher linear mit der Erhöhung gestiegen sind).

• Zu k) Richtig ist, dass Einzelkosten sowohl einzelnen Produkten, aber möglicherweise auch Produktgruppen, Aufträgen, Kunden oder Kostenstellen unmittelbar direkt zugeordnet werden können. Bei der Definition von Einzelkosten kommt es auf die dazugehörige Bezugsgröße an.

• Zu m) Würden die Kosten in absoluter Höhe nur linear ansteigen, dann blieben die Stückkosten konstant (siehe Antwort zu Aussage a). Da die Kosten aber überproportional wachsen, steigen die Stückkosten ebenfalls an.

• Zu o) Richtig wäre das Verursachungsprinzip.

• Zu p) Im Gegenteil, eine Plankostenrechnung ist aufgrund des vorausgehenden notwendigen Planungs- und Budgetprozesses sehr aufwändig.

• Zu q) Richtig wäre hier die Stückerfolgsrechnung.

Bevor wir zu den eigentlichen Kostenrechnungsaufgaben dieses Kapitels kommen, soll an dieser Stelle, quasi als Wiederholung des schulischen Mathematikunterrichts, die Vorgehensweise beim Aufteilen von Beträgen in bestimmten vorgegebenen Verhältnissen beschrieben werden. Eine typische Aufgabenstellung wäre z. B. das Aufteilen eines Betrages von 6.000 € im Verhältnis von 1 zu 2 zu 5 auf 3 Personen (offensichtlich falsch wäre es ja, hier jeder Person 2.000 € zu geben).

Ein mathematisches Verhältnis ist die Beziehung zwischen zwei Zahlen. Dieses Verhältnis wird meist als deren Quotient ausgedrückt. So stehen bspw. die Zahlen a und b in einem Verhältnis von . Dabei werden a und b als Verhältnisglieder bezeichnet. In einer alternativen Darstellungsweise kann man dann auch sagen, das Verhältnis ist »a zu b« oder a:b oder a/b. Bei mehr als zwei Zahlen, z. B. a, b, c und d stellt man das Verhältnis als »a zu b zu c zu d« oder als a:b:c:d oder seltener als a/b/c/d dar. Die Bruchdarstellung wird dann nicht mehr gewählt.

Soll nun ein Betrag W in bestimmten Verhältnissen aufgeteilt werden, sind im ersten Schritt alle Verhältnisglieder hochzuaddieren, also z. B. bei vier Verhältnisgliedern die Summe

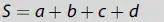
zu bilden.

Im zweiten Schritt werden dann die einzelnen Verhältnisglieder jeweils durch die Summe S geteilt und dann mit dem Wert W multipliziert. Die Aufteilung von W ergibt dann also bspw. bei vier Verhältnisgliedern a, b, c, d die Aufteilung in folgende vier Teile:

In obigem Zahlenbeispiel wäre also im ersten Schritt die Summe aus 1 und 2 und 5 zu bilden, d. h. 1 + 2 + 5 = 8. Dann erhalten die drei Personen die folgenden Beträge:

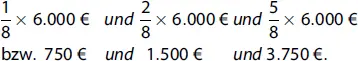
Diese Ergebnisse stehen ebenso im Verhältnis von 1 zu 2 zu 5 zueinander. D.h. 1.500 € ist zweimal so viel wie 750 € und 3.750 ist 5mal so viel wie 750 €.

a) Eine Kalkmörtelmischung besteht aus drei Teilen Sand, einem Teil Kalk und einem halben Teil Wasser. Wieviel kg dieser Rohstoffe müssen jeweils zusammengemischt werden, falls daraus 27 kg Mörtel entstehen sollen?

b) Ein großes Bauunternehmen hat drei Profitcenter: Hochbau (Umsatz 230 Mio. €), Tiefbau (Umsatz 150 Mio. €) und Bauinstallation (Umsatz 450 Mio. €). Da alle drei Profitcenter an der Durchführung eines Großauftrages beteiligt waren, soll dessen Gewinn von 498.000 € nach deren Umsatz auf diese drei Profitcenter aufgeteilt werden. Wieviel Gewinn erhält jedes der Profitcenter?

a) Schritt 1 – Addition der Verhältnisglieder, d. h. der genannten Bestandteile 3 + 1 + 0,5 = 4,5.

Schritt 2 – Errechnung der Rohstoffmengen mit

Sand: 3 ÷ 4,5 × 27 kg = 18 kg, Kalk: 1 ÷ 4,5 × 27 kg = 6 KG, Wasser: 0,5 ÷ 4,5 × 27 kg = 3 kg.

b) Schritt 1 – Addition der Verhältnisglieder, d. h. der Umsätze der drei Profitcenter: 230 Mio. € + 150 Mio. € + 450 Mio. € = 830 Mio. €.

Schritt 2 - Errechnung der zugeordneten Gewinnanteile:

Hochbau: 230 Mio. € ÷ 830 Mio. € × 498.000 € = 138.000 €

Tiefbau: 150 Mio. € ÷ 830 Mio. € × 498.000 € = 90.000 €

Bauinstallation: 450 Mio. € ÷ 830 Mio. € × 498.000 € = 270.000 €.

Natürlich kann man diese Art von Aufgaben auch über eine Prozentrechnung lösen ( Kap. 3.3.2 ). Hierzu wäre bspw. bei der Aufgabe b) der Gesamtumsatz der drei Profitcenter zu bestimmen und dann zu ermitteln, wieviel Prozent davon die jeweiligen Profitcenter ausmachen. Mit diesen Prozentsätzen wären dann die Gewinne aufzuteilen.