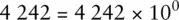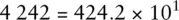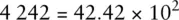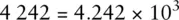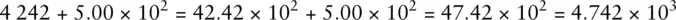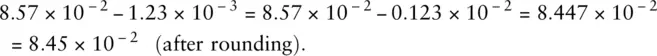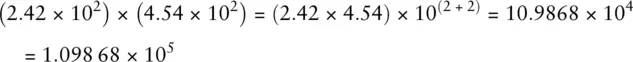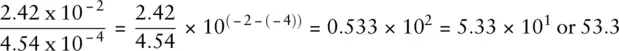1 ...7 8 9 11 12 13 ...28
0.6 Calculations using scientific notation
0.6.1 Adding and subtracting
When adding numbers expressed using scientific notation, it is often useful to write the numbers using non‐standard coefficients to simplify the mathematical process.
For example, the number 4 242 can be written in any of the following ways and retains its original numerical value:
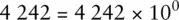
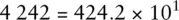
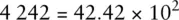
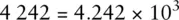
Only the last figure is standard scientific notation. However, if we were required to add the number 4 242 to 5.00 × 10 2and give the answer in standard scientific notation, the following procedure could be used:
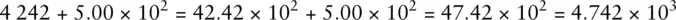
The example shows that the numbers are converted such that the exponent is common, i.e. 10 2in this case, and then the numbers can be added.
Similarly, with numbers smaller than 1, the values are converted such that the exponents are common and added or subtracted in the normal manner. The exponent remains unchanged.
For example:
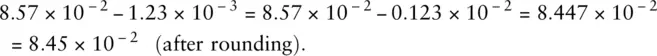
In this example the numbers are exact, that means we know them precisely. For example the number of people in a room. We therefore don’t need to give the answer to a specific number of significant figures as, effectively, the number of significant figures is infinite.
This answer must be rounded, as we only know the original values to an accuracy of three significant figures.
Calculate the values of the following, giving your answers in scientific notation:
1 102 + 1.310 × 103 =
2 0.057 90 + 1.3 × 10−4 =
3 3.120 × 10−2 − 5.7 × 10−4 =
4 6.375 × 103 − 0.103 × 102 =
1 Express both numbers in a format that has the same exponent, and then add:
2 Express both numbers in a format that has the same exponent, and then subtract:
3 Express both numbers in a format that has the same exponent, and then subtract:
4 Express both numbers in a format that has the same exponent, and then subtract:
0.6.2 Multiplying and dividing numbers
When multiplying numbers written in scientific notation, the coefficients (i.e. the numbers in front of the 10 n) are multiplied and the exponents are added. So, for example:
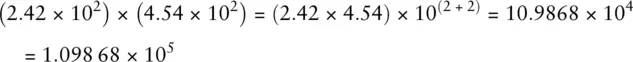
When dividing numbers written in scientific notation, the coefficients are divided and the exponents subtracted. So, for example:
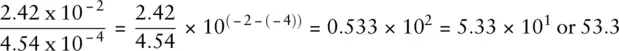
Calculate the answers to the following expressions, and present your result in scientific notation:
1 7.5 × 5.7 =
2 (6.4 × 102) × (1.30 × 104) =
3 (1.751 × 10−3) × (59.0 × 10−2) =
4 1.435 × 10−2 ÷ 2.9 × 10−4 =
1 7.5 × 5.7 = 42.75 = 43 = 4.3 × 101The smallest number of significant figures is two, so this becomes 43 after reducing the number of significant figures and rounding.
2 (6.4 × 102) × (1.30 × 104) = 8.32 × 106 = 8.3 × 106The smallest number of significant figures is two, so 8.32 becomes 8.3 after reducing the number of significant figures.
3 (1.751 × 10−3) × (59.0 × 10−2) = 103.309 × 10−5 = 1.033 09 × 10−3 = 1.03 × 10−3The smallest number of significant figures is three, so 1.03309 becomes 1.03 after reducing the number of significant figures.
4 = 4.9 × 101The smallest number of significant figures is two, so 4.948 × 101 becomes 4.9 × 101 after reducing the number of significant figures and rounding down. This would normally be written as 49.
0.7 Writing chemical formulae and equations
0.7.1 Writing chemical formulae
Most people are familiar with H 2O and CO 2as the formulae that represent water and carbon dioxide, respectively.
A chemical compound has a formula that represents the type and number of atoms in that compound. The plural of ‘formula’ is ‘formulae’ as the word derives from Latin.
The letters in the formulae represent the elements in the periodic table, and the numbers given as subscripts after the letters indicate how many atoms of each element are in one unit of the compound. The formula H 2O tells us there are two atoms of hydrogen (H) and one atom of oxygen (O) in one molecule of the compound. In CO 2,there is one atom of carbon and two atoms of oxygen.
The terms ‘atom’ and ‘molecule’ will be explained fully in Chapter 1.
In the formulae of some compounds, there may be atoms enclosed in brackets (or parentheses): for example, Ca(NO 3) 2, the formula for calcium nitrate. The formula indicates that in one formula unit of calcium nitrate, there is one atom of calcium (Ca), two atoms of nitrogen (N), and six atoms of oxygen (O). The brackets act as a multiplier, multiplying all the atoms inside the bracket by the number in subscript outside the bracket.
Substances such as calcium nitrate, Ca(NO 3) 2, are known as salts. These are composed of ions. Ions are atoms, or groups of atoms, that have an overall charge. The charge can be positive or negative. A positively charged ion is known as a cation. A negatively charged ion is known as an anion. Table 0.4lists some common cations and anions. You will see that most cations are actually metal ions.
Table 0.4Symbols and charges for some common cations and anions.
| Common cations |
Common anions |
| Symbol |
Name |
Charge |
Symbol |
Name |
Charge |
| Na + |
Sodium |
+1 |
F − |
Fluoride |
−1 |
| K + |
Potassium |
+1 |
Cl − |
Chloride |
−1 |
| Mg 2+ |
Magnesium |
+2 |
Br − |
Bromide |
−1 |
| Ca 2+ |
Calcium |
+2 |
O 2− |
Oxide |
−2 |
| Al 3+ |
Aluminium |
+3 |
S 2− |
Sulfide |
−2 |
| Cu 2+ |
Copper |
+2 |
CO 3 2− |
Carbonate |
−2 |
| Fe 2+ |
Iron |
+2 |
SO 4 2− |
Sulfate |
−2 |
| Ag + |
Silver |
+1 |
NO 3 − |
Nitrate |
−1 |
| Zn 2+ |
Zinc |
+2 |
PO 4 3− |
Phosphate |
−3 |
| NH 4 + |
Ammonium |
+1 |
OH − |
Hydroxide |
−1 |
Salts are neutral substances made up of positive cations and negative anions in a ratio that ensures the overall charge on the salt is zero. For example, aluminium sulfate is composed of aluminium (Al 3+) ions and sulfate (SO 4 2−) ions. Because the salt is neutral overall, the formula must be Al 2(SO 4) 3.
Читать дальше