When a number is written in exponential form, it is called scientific notation. The standard format is that the number is written with one digit before the decimal point and the multiplier 10 nis added after the number. The following examples show how numbers can be rewritten using scientific notation:
4 is written as 4 × 100.Any number raised to the power of zero is equal to 1, so 100 = 1.
42 is written as 4.2 × 101.It isn't usual to use the factors 100 and 101 unless specifically required to give an answer in scientific notation.
242 is written as 2.42 × 102.
2424 is written as 2.424 × 103.
To express numbers smaller than 1 using scientific notation, i.e. a decimal number, the number is converted to a number between 1 and 10 and the exponential factor 10 –nused to indicate the position of the decimal point, as in these examples:
0.4 is written as 4 × 10−1.
0.042 is written as 4.2 × 10−2.
0.00242 is written as 2.42 × 10−3.
When converting numbers that are less than 1 expressed in scientific notation back to decimal numbers, move the decimal point to the left by the value of the exponent, adding zeroes. So 2.42 × 10 −3moves the decimal point by three places to the left, requiring two zeroes after the decimal point.

Write the following numbers expressed in non‐exponential form using scientific notation:
1 675
2 1 000 000
3 0.98
4 0.00355
1 To write 675 in scientific notation, we must move the decimal point (currently after the 5) two spaces to the left (i.e. divide by 100) and then multiply the remaining number by 100 or 102.675 becomes 6.75 × 102.
2 To write 1 000 000 in scientific notation, we must move the decimal point (currently after the last 0) six spaces to the left (i.e. divide by 1 000 000) and then multiply the remaining number by 1 000 000 or 106.1 000 000 becomes 1 × 106.
3 To write 0.98 in scientific notation, we must move the decimal point one space to the right (i.e. multiply by 10) and then multiply the remaining number by 0.1 or 10−1 (i.e. divide by 10).So 0.98 becomes 9.8 × 10−1.
4 To write 0.00355 in scientific notation, we must move the decimal point three spaces to the right (i.e. multiply by 1 000) and then multiply the remaining number by 0.001 or 10−3 (i.e. divide by 1 000).So 0.00355 becomes 3.55 × 10−3.
Convert the following numbers, expressed in scientific notation, to non‐exponential form.
1 7.01 × 102
2 6.912 × 105
3 8.05 × 10−1
4 2.310 × 10−4
1 Move the decimal point to the right by the number of spaces indicated by the exponent, i.e. by 2. 7.01 becomes 701.
2 Move the decimal point to the right by the number of spaces indicated by the exponent, i.e. by 5. 6.912 × 105 becomes 691 200.
3 Move the decimal point to the left by the number of spaces indicated by the exponent, i.e. by 1 space. 8.05 × 10−1 becomes 0.805.
4 Move the decimal point to the left by the number of spaces indicated by the exponent, i.e. by 4 spaces. 2.310 × 10−4 becomes 0.0002310.
0.4 Using metric prefixes
Scientists also have a shorthand for writing some large and small numbers using a prefix that represents a certain quantity. So the quantity 1 000 g, or 1 × 10 3g in scientific notation, can be written as 1 kg. The letter ‘k’ represents the factor ‘kilo’, or 10 3. The quantity one‐thousandth of a gram or 0.001 g (1 × 10 −3g) can be written as 1 mg, where the prefix ‘m’ represents the factor ‘milli’, or 10 −3. Table 0.3gives some common prefixes, along with their symbols.
Note that the ‘k’ in kg is lowercase. The case of the unit can be very important, so make sure you pay attention to it!
Table 0.3Some common prefixes and their values with quantities and symbols.
| Factor |
Number |
Name |
Symbol |
Factor |
Number |
Name |
Symbol |
| 10 9 |
1 000 000 000 |
giga |
G |
10 −9 |
0.000 000 001 |
nano |
n |
| 10 6 |
1 000 000 |
mega |
M |
10 −6 |
0.000 001 |
micro |
μ |
| 10 3 |
1 000 |
kilo |
k |
10 −3 |
0.001 |
milli |
m |
|
|
|
|
10 −2 |
0.01 |
centi |
c |
|
|
|
|
10 −1 |
0.1 |
deci |
d |
0.4.1 Units of mass and volume used in chemistry
Mass
The massof a substance is the amount we measure when we weigh the substance. Mass is a measure of the quantity of a substance. In science, we use the term massas opposed to weightof a substance to describe the amount because the weight of a substance is related to the gravitational force acting on the substance. We often use the words ‘mass’ and ‘weight’ interchangeably, but they are not really the same thing scientifically.
The SI unit of mass is the kilogram. However, in the laboratory, chemicals and other objects are usually weighed in units of grams as the gram is a far more convenient amount to work with. Even though we use a balance to weigha substance, we report its massin grams, not its weight.
One kilogram is equivalent to one thousand grams, 1 000 g. 1 kg = 1 000 g. Therefore 1 g = 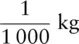 or 0.001 kg. This can also be written as 1 × 10 −3kg.
or 0.001 kg. This can also be written as 1 × 10 −3kg.
Another common measure of mass is the milligram, mg. One milligram is one‐thousandth of a gram:
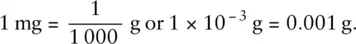
You should always choose a balance appropriate to the level of accuracy of the mass required. If you need ‘about two grams’, for example, a two‐figure balance is perfectly appropriate. If you are told to weigh ‘accurately approximately two grams’, this implies you need to use a four‐figure balance to weigh around two grams of substance but record its weight accurately to four decimal places, e.g. 0.0001 g.
The volume of a substance is the space that it occupies. In chemistry, we are generally most concerned with the volumes of liquids and gases.
Liquid volumes are measured relatively easily, and the type of measuring device used will depend upon the accuracy with which we need to know the volume. There is always a certain amount of uncertainty when making a measurement. Different types of measuring equipment have different levels of uncertainty associated with them. For less accurate work, chemists generally use a measuring cylinder ( Figure 0.2a). These can be obtained in different sizes, but the uncertainty in the volume when using a measuring cylinder depends on the size of the measuring cylinder and the graduations. The uncertainty on a measuring cylinder is half the volume of the smallest graduations. For a 25 cm 3measuring cylinder where the graduations are 0.5 cm 3, the uncertainty is ±0.25 cm 3. If 25 cm 3was measured into a 25 cm 3measuring cylinder, the percentage uncertainty would be 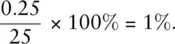 If a 250 cm 3measuring cylinder was used to measure out 25 cm 3where the uncertainty was ±0.5 cm 3, the percentage uncertainty would be
If a 250 cm 3measuring cylinder was used to measure out 25 cm 3where the uncertainty was ±0.5 cm 3, the percentage uncertainty would be  = 2%. It is therefore more accurate to use a smaller measuring cylinder for this volume of liquid.
= 2%. It is therefore more accurate to use a smaller measuring cylinder for this volume of liquid.
Читать дальше


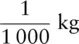 or 0.001 kg. This can also be written as 1 × 10 −3kg.
or 0.001 kg. This can also be written as 1 × 10 −3kg.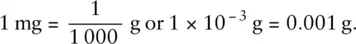
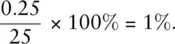 If a 250 cm 3measuring cylinder was used to measure out 25 cm 3where the uncertainty was ±0.5 cm 3, the percentage uncertainty would be
If a 250 cm 3measuring cylinder was used to measure out 25 cm 3where the uncertainty was ±0.5 cm 3, the percentage uncertainty would be  = 2%. It is therefore more accurate to use a smaller measuring cylinder for this volume of liquid.
= 2%. It is therefore more accurate to use a smaller measuring cylinder for this volume of liquid.










