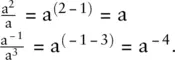0.2 Measurement in chemistry and science – SI units
Chemistry is a practical subject, and our present knowledge of chemical properties and principles is based on experiments. Unfortunately, we don't have space in this book to describe many of the amazing experiments that early investigators carried out to enhance our understanding and knowledge of chemistry. The majority of experiments require making and recording measurements. The laws of science operate across the globe, so it's important that scientists make measurements that can be compared with each other. Therefore, measurements must be recorded in a universal and standard way. For this reason, the metric system was developed to establish a standardised set of units. The metric system has its origins in the eighteenth century. More recently, a revised metric system was introduced and adopted by scientists across the world. This system is known as the Système Internationale d'Unités, and the units in the system are known as SI units.
There are seven fundamental SI units. Six of these are commonly used in chemistry, and you will meet all of them in this course. The six base unitsused in chemistry are listed in Table 0.1and are the units of mass, length, time, electrical current, temperature, and amount of substance. All other units for physical quantities can be reduced to these base units. For example, speed is defined as the distance or length travelled divided by the time taken, so:
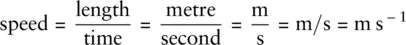
Table 0.1Base SI quantities used in chemistry with symbols and units.
| Physical quantity |
Symbol |
Base unit |
Unit symbol |
| Mass |
m |
kilogram |
kg |
| Length |
l |
metre |
m |
| Time |
t |
second |
s |
| Electrical current |
I |
ampere |
A |
| Temperature |
T |
kelvin |
K |
| Amount of substance |
n |
mole |
mol |
This defines the unit of speed as metre per second or m/s. In chemistry, as in most other scientific subjects, this would be written as: m s −1, where the superscript ‘−1’ means ‘per second’.
There are many other units you will come across that can be reduced down to these base units. Units of this type are called derived unitsand usually have their own symbol. A list of derived units and their symbols is given in Table 0.2.
Dealing with exponents
Exponents tell us how many times a number should be multiplied by itself. For example:
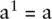
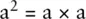
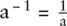
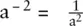 A special case is a 0= 1 To multiply quantities with exponents just add the exponents together:
A special case is a 0= 1 To multiply quantities with exponents just add the exponents together: 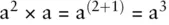
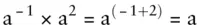 To divide quantities with exponents subtract the exponents:
To divide quantities with exponents subtract the exponents: 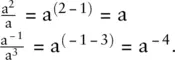
Table 0.2Commonly used derived units.
| Quantity |
Unit name |
Symbol and base units |
| Area |
square metre |
m 2 |
| Volume |
cubic metre |
m 3 |
| Velocity (speed) |
metre per second |
m s −1 |
| Acceleration |
metre per second squared |
m s −2 |
| Density |
kilogram per cubic metre |
kg m −3 |
| Concentration |
mole per cubic metre |
mol m −3 |
| Energy |
joule |
J = kg m 2s −2 |
| Force |
newton |
N = J m −1= kg m s −2 |
| Pressure |
pascal |
Pa = N m −2= kg m −1s −2 |
| Frequency |
hertz |
Hz = s −1 |
It is very important when carrying out calculations to keep track of the units, as you will be expected to quote the units of your answers. Units of each value in a calculation multiply or cancel with each other, as shown in the example here:
Acceleration is defined as the change in velocity (speed) divided by the time taken and can be represented by this equation: acceleration = .
Replacing the quantities with their units, we obtain: acceleration = .
The unit can also be written as s−1, so the units for acceleration are m s−1 × s−1.
To multiply s−1 by s−1, we simply add the −1 superscripts: acceleration = m s−1 × s−1 = m s−2.
If we know the speed of an object and wish to determine how far it travels in a certain time, we multiply the speed by the time: distance = speed × time.
Inserting the units for speed and time gives us the unit for distance = m s−1 × s.
To multiply s−1 by s, again we add the superscripts: distance = m s−1 × s = m. This gives us the answer for distance in the correct units of metres. You should always check your answer when doing calculations to make sure that the value you obtain and the units are sensible.
Determine the derived units for the following quantities using the definitions given:
1 density =
2 entropy =
3 pressure =
4 power =
1 density = = kg m−3
2 entropy = = = kg m2 s−2 K−1
3 pressure = = = = kg m s−2 × m−2 = kg m−1 s−2
4 power = = = = kg m2 s−2 × s−1 = kg m2 s−3
0.3 Expressing large and small numbers using scientific notation
When studying science, you will likely come across numbers that are either extremely large or very small. It often isn't convenient (or practical) to write out the numbers ‘longhand’. An example of this is in using the constant for the speed of light in vacuum. The value of this constant is approximately three hundred million metres per second (m s −1), which can be written as 300 000 000 m s −1. This method of writing numbers is sometimes called non‐exponential form. A much simpler way of expressing this number is in exponential form,so 300 000 000 m s −1is written as 3 × 10 8m s −1. The number 10 8represents one hundred million or 100 000 000. When is it written as × 10 8this means there are eight zeroes after the 3. Some numbers are very small: for example, the Planck constant is 6.6 × 10 −34J s. The number 10 −34indicates there are 33 zeroes after the decimal point and before the number itself. Clearly, it would be very tedious to write the number out in full!
Take care!
3 × 10 2= 300 (i.e. two zeroes after the number before the decimal point) 3 × 10 −2= 0.03 (i.e. just one zero after the decimal point before the number)
Читать дальше

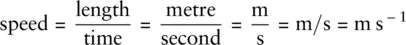
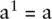
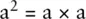
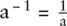
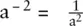 A special case is a 0= 1 To multiply quantities with exponents just add the exponents together:
A special case is a 0= 1 To multiply quantities with exponents just add the exponents together: 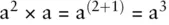
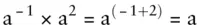 To divide quantities with exponents subtract the exponents:
To divide quantities with exponents subtract the exponents: