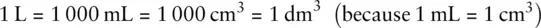1 ...6 7 8 10 11 12 ...28 
Figure 0.2(a) 25 cm 3measuring cylinder; (b) 25 cm 3pipette; (c) 50 cm 3burette.
Source: Eisco Labs.
If we need to know the volume of liquid measured more accurately than this, either a pipette or a burette can be used. A pipette ( Figure 0.2b) measures a fixed volume of liquid, and pipettes can be obtained in various sizes. A burette ( Figure 0.2c) can be used to deliver variable volumes of liquids; although burettes can be obtained in various sizes, the 50 cm 3burette is the size most commonly used. The uncertainty on a volume measurement when using a laboratory pipette is ±0.06 cm 3. This means the uncertainty on measuring a volume of 25 cm 3using a pipette is 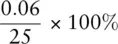 = 0.2%. For a standard burette, the uncertainty associated with each reading is ±0.05 cm 3. If making one reading, then the percentage uncertainty in measuring 25 cm 3is
= 0.2%. For a standard burette, the uncertainty associated with each reading is ±0.05 cm 3. If making one reading, then the percentage uncertainty in measuring 25 cm 3is 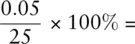 0.2%. When recording the amount added from a burette, we make two readings, so the total uncertainty associated with the readings is ±0.1 cm 3. Thus the percentage uncertainty on the burette reading is
0.2%. When recording the amount added from a burette, we make two readings, so the total uncertainty associated with the readings is ±0.1 cm 3. Thus the percentage uncertainty on the burette reading is 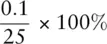 = 0.4%.
= 0.4%.
The derived SI unit for volume is the cubic metre or m 3because the volume of an object is obtained from the product of its height, width, and depth, which are all units of length ( Figure 0.3a). As the SI unit of length is the m, the derived unit for volume has units of m 3. However, a volume of 1 m 3is very large, so the m 3is not a very useful unit.
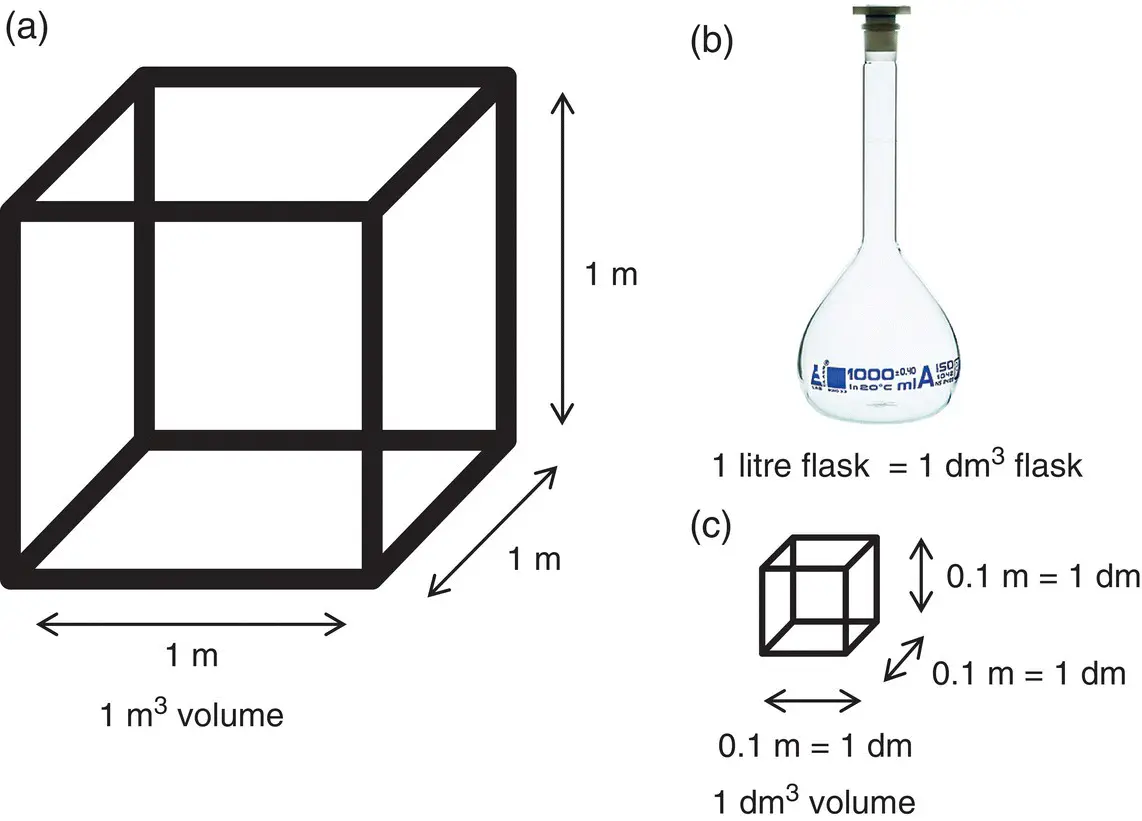
Figure 0.3(a) Cube of volume 1 m 3. (b) Flask of volume 1 L.
Source: Eisco Labs.
(c) Cube of volume 1 dm 3, not to scale.
In the chemistry laboratory, we often work with volumes a lot smaller than a cubic metre. A volume you will often encounter is the litre ( Figure 0.3b). The symbol that represents the litre is L. However, strictly speaking, this is a non‐SI unit, although it is in common use. Chemists usually work in volumes of cm 3or dm 3where:
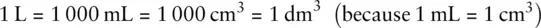
Therefore: 1 L = 1 dm 3.
1 dm (decimetre) = 0.1 m (1 × 10 −1m) ( Figure 0.3c).
Remember
1 dm 3= 1 L = 1 x 10 −3m 31 000 dm 3= 1 000 L = 1 m 3.
1 dm 3(decimetre cubed) = (0.1 m) 3= ( 1 × 10 −1m) 3= 1 × 10 −3m 3.
1 dm 3is therefore one thousandth of a m 3. There are therefore 1 000 dm 3or 1 000 L in 1 m 3.
Imagine the size of a 1 litre carton of orange juice. 1 000 cartons of 1 litre orange juice would fit in a cubic metre.

Source: Dr Elizabeth Page.
Convert each of the following masses to grams. You may need to refer to Table 0.3to obtain the numerical values of the prefixes used. Give your answers in scientific notation:
1 2.32 Mg
2 1 000 mg
3 400 μg
1 2.32 Mg = 2.32 × 106 g
2 1 000 mg = 1 000 × 10−3 g = 1 g
3 400 μg = 400 × 10−6 g = 4.00 × 10−4 g
Express the following quantities in the units stated:
1 1 cm3 in m3
2 1 000 m3 in dm3
3 1 g m−3 in g dm−3
1 1 cm is the same as 0.01 m or 1 × 10−2 m.Therefore 1 cm3 = (0.01 m)3 = (1 × 10−2)3 m3 = 1 × 10−6 m3
2 1 m is 10 times bigger than 1 dm: 1 m = 10 dm.Therefore 1 m3 = 1 × 103 dm3.1 m3 is 1 × 103 (one thousand) times bigger than 1 dm3.Therefore 1 000 m3 = 1 000 × 103 dm3 = 1 × 106 dm3.
3 1 dm3 is one‐thousandth of a m3.If the concentration is equal to 1 g in 1 m3, there will be 1 000 times fewer grams in 1 dm3.So 1 g m−3 = 1 × 10−3 g dm−3.
When carrying out calculations in science, the answer must be given to the same level of accuracy as the values in the question. For example, if a balance weighs to two decimal places, the mass of substance weighed may be read as 5.02 g. The total number of significant figures in this number is three. This means we know the mass accurate to 3 significant figures.
The number can be rounded to a smaller number of significant figures as shown:
Three significant figures = 5.02 g
Two significant figures = 5.0 g
One significant figure = 5 g
An answer should be given to the same number of significant figures as the number with fewest significant figures in the calculation. For example, if the mass of solid is 5.02 g and the mass of water the solid is added to is 50 g (the same as 50 mL or 50 cm 3), the total mass of the solid and water would be 5.02 g + 50 g = 55 g. The answer can only be given to two significant figures as the mass of water is only known to this level of accuracy. In fact, the mass of water could actually be any mass between 49.50 g and 50.49 g, which are both equivalent to 50 g when given to two significant figures.
There are some rules for determining how many significant figures are in a number:
1 Any zeroes before a digit are not significant. For example, 0.005 is only accurate to 1 significant figure.
2 Any zeroes after a digit are significant. For example, 0.00500 is accurate to 3 significant figures.
3 Digits below the number 5 are always rounded downwards, and digits equal to or above the number 5 are rounded upwards, as in the following examples:The number 0.544 becomes 0.54 when written to two significant figures.The number 0.545 becomes 0.55 when written to two significant figures.The number 0.546 becomes 0.55 when written to two significant figures.
4 When performing a calculation, determine the required number of significant figures and round up or down at the end of the calculation, not at the steps in between.
5 Always give your answer to the same accuracy as that of the value known to the least number of significant figures in the calculation.
Convert the following numbers to values with two significant figures, and write the answer in scientific notation:
1 9 495 g
2 0.00940 g
3 0.09056 g
4 19.005 g + 1.515 g
1 9 495 g has four significant figures and becomes 9 500 g to two significant figures. In scientific notation, this is written as: 9.5 × 103 g.
2 0.00940 g has three significant figures and becomes 0.0094 g to two significant figures. In scientific notation, this is written as: 9.4 × 10−3 g.
3 0.09056 g has four significant figures and becomes 0.091 g to two significant figures when rounded up. In scientific notation, this is written as: 9.1 × 10−2 g.
4 The sum of 19.005 g + 1.515 g is 20.520 g, but this value has five significant figures. When it is rounded to two significant figures, it becomes 21 g as 0.52 rounds up to 1.0.
Читать дальше


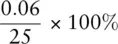 = 0.2%. For a standard burette, the uncertainty associated with each reading is ±0.05 cm 3. If making one reading, then the percentage uncertainty in measuring 25 cm 3is
= 0.2%. For a standard burette, the uncertainty associated with each reading is ±0.05 cm 3. If making one reading, then the percentage uncertainty in measuring 25 cm 3is 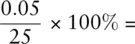 0.2%. When recording the amount added from a burette, we make two readings, so the total uncertainty associated with the readings is ±0.1 cm 3. Thus the percentage uncertainty on the burette reading is
0.2%. When recording the amount added from a burette, we make two readings, so the total uncertainty associated with the readings is ±0.1 cm 3. Thus the percentage uncertainty on the burette reading is 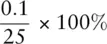 = 0.4%.
= 0.4%.