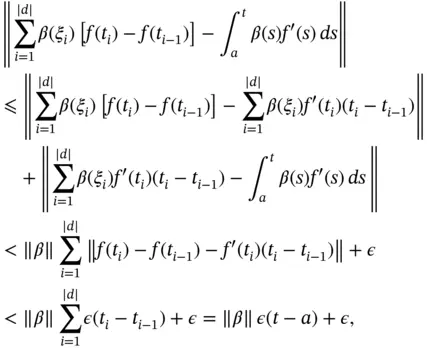
by (1.18)and by the Riemann integrability of 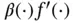 . Finally, (1.13)follows from (1.16)and (1.17)and the proof is complete.
. Finally, (1.13)follows from (1.16)and (1.17)and the proof is complete.

1.3.5 A Convergence Theorem
As the last result of this introductory chapter, we mention a convergence theorem for Perron–Stieltjes integrals. Such result is used in Chapter 3. A proof of it can be found in [180, Theorem 2.2].
Theorem 1.88: Consider functions and , for . Suppose
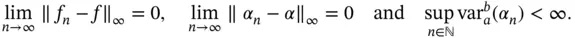
Then
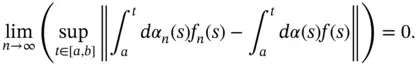
Appendix 1.A: The McShane Integral
The integrals introduced by J. Kurzweil [152] and independently by R. Henstock [118] in the late 1950s are equivalent to the restricted Denjoy integral and the Perron integral for integrands taking values in 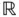 (see [108], for instance). In particular, the definitions of the so-called ”Kurzweil–Henstock” integrals are based on Riemannian sums, and are therefore easy to deal with even by undergraduate students. Not only that, but the Kurzweil–Henstock–Denjoy–Perron integral encompasses the integrals of Newton, Riemann, and Lebesgue.
(see [108], for instance). In particular, the definitions of the so-called ”Kurzweil–Henstock” integrals are based on Riemannian sums, and are therefore easy to deal with even by undergraduate students. Not only that, but the Kurzweil–Henstock–Denjoy–Perron integral encompasses the integrals of Newton, Riemann, and Lebesgue.
In 1969, E. J. McShane (see [173, 174]) showed that a small change in the subdivision process of the domain of integration within the Kurzweil–Henstock (or Perron) integral leads to the Lebesgue integral. This is a very nice finding, since now the Lebesgue integral can be taught by presenting its Riemannian definition straightforwardly and, then, obtaining immediately some very interesting properties such as the linearity of the Lebesgue integral which comes directly from the fact that the Riemann sum can be split into two sums. The monotone convergence theorem for the Lebesgue integral is another example of a result which is naturally obtained from its equivalent definition due to McShane.
The Kurzweil integral and the variational Henstock integral can be extended to Banach space-valued functions as well as to the evaluation of integrands over unbounded intervals. The extension of the McShane integral, proposed by R. A. Gordon (see [107]) to Banach space-valued functions, gives a more general integral than that of Bochner–Lebesgue. As a matter of fact, the idea of McShane into the definition due to Kurzweil enlarges the class of Bochner–Lebesgue integrals.
On the other hand, when the idea of McShane is employed in the variational Henstock integral, one gets precisely the Bochner–Lebesgue integral. This interesting fact was proved by W. Congxin and Y. Xiabo in [47] and, independently, by C. S. Hönig in [131]. Later, L. Di Piazza and K. Musal generalized this result (see [55]). We clarify here that unlike the proof by Congxin and Xiabo, based on the Fréchet differentiability of the Bochner–Lebesgue integral, Hönig's idea to prove the equivalence between the Bochner–Lebesgue integral and the integral we refer to as Henstock–McShane integral uses the fact that the indefinite integral of a Henstock–McShane integrable function is itself a function of bounded variation and the fact that absolute Henstock integrable functions are also functions of bounded variation. In this way, the proof provided in [131] becomes simpler. We reproduce it in the next lines, since reference [131] is not easily available. We also refer to [73] for some details.
Definition 1.89:We say that a function 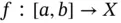 is Bochner–Lebesgue integrable (we write
is Bochner–Lebesgue integrable (we write 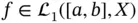 ), if there exists a sequence
), if there exists a sequence 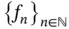 of simple functions,
of simple functions, 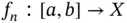 ,
, 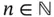 , such that
, such that
1 almost everywhere (i.e. for almost every ), and
2 .
With the notation of Definition 1.89, we define
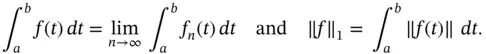
Then, the space of all equivalence classes of Bochner–Lebesgue integrable functions, equipped with the norm  , is complete.
, is complete.
The next definition can be found in [239], for instance.
Definition 1.90:We say that a function 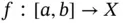 is measurable , whenever there is a sequence of simple functions
is measurable , whenever there is a sequence of simple functions 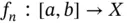 such that
such that 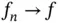 almost everywhere. When this is the case,
almost everywhere. When this is the case,
(1.A.1) 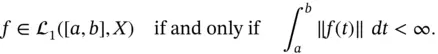
Again, we explicit the “name” of the integral we are dealing with, whenever we believe there is room for ambiguity.
As we mentioned earlier, when only real-valued functions are considered, the Lebesgue integral is equivalent to a modified version of the Kurzweil–Henstock (or Perron) integral called McShane integral . The idea of slightly modifying the definition of the Kurzweil–Henstock integral is due to E. J. McShane [173, 174]. Instead of taking tagged divisions of an interval 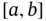 , McShane considered what we call semitagged divisions , that is,
, McShane considered what we call semitagged divisions , that is,
Читать дальше

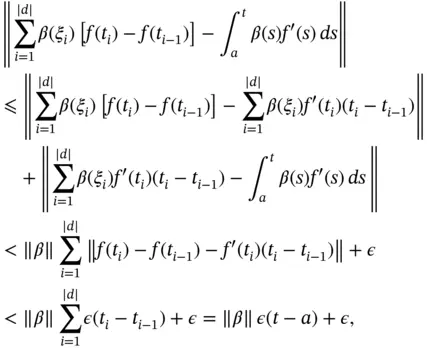
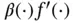 . Finally, (1.13)follows from (1.16)and (1.17)and the proof is complete.
. Finally, (1.13)follows from (1.16)and (1.17)and the proof is complete.
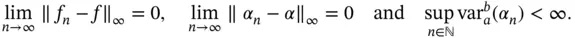
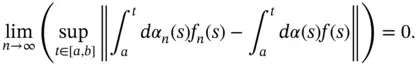
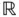 (see [108], for instance). In particular, the definitions of the so-called ”Kurzweil–Henstock” integrals are based on Riemannian sums, and are therefore easy to deal with even by undergraduate students. Not only that, but the Kurzweil–Henstock–Denjoy–Perron integral encompasses the integrals of Newton, Riemann, and Lebesgue.
(see [108], for instance). In particular, the definitions of the so-called ”Kurzweil–Henstock” integrals are based on Riemannian sums, and are therefore easy to deal with even by undergraduate students. Not only that, but the Kurzweil–Henstock–Denjoy–Perron integral encompasses the integrals of Newton, Riemann, and Lebesgue.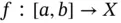 is Bochner–Lebesgue integrable (we write
is Bochner–Lebesgue integrable (we write 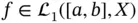 ), if there exists a sequence
), if there exists a sequence 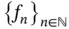 of simple functions,
of simple functions, 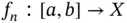 ,
, 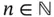 , such that
, such that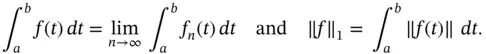
 , is complete.
, is complete.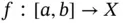 is measurable , whenever there is a sequence of simple functions
is measurable , whenever there is a sequence of simple functions 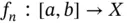 such that
such that 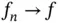 almost everywhere. When this is the case,
almost everywhere. When this is the case,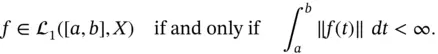
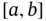 , McShane considered what we call semitagged divisions , that is,
, McShane considered what we call semitagged divisions , that is,










