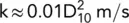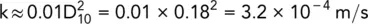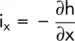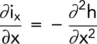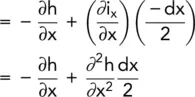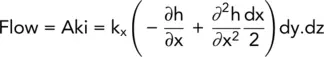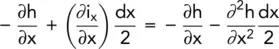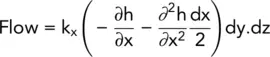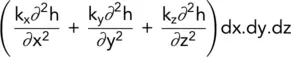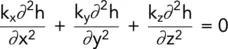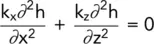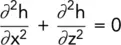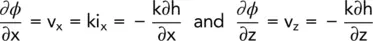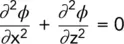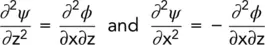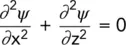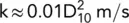
where D 10= effective size in mm.
Wise (1992) offered approximations for other soils based on pore size distribution but it should be remembered that no formula is as good as an actual permeability test.
Typical ranges of coefficient of permeability
Gravel >10−1 m/s
Sands 10−1–10−5 m/s
Fine sands, coarse silts 10−5–10−7 m/s
Silts 10−7–10−9 m/s
Clays <10−9 m/s
Example 2.4 Approximation of k
Calculate an approximate value for the coefficient of permeability for the soil in Example 1.2.
Solution:
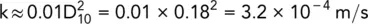
2.8 General differential equation of flow
Figure 2.7shows an elemental cube, of dimensions d x, d y, and d z, in an orthotropic soil with an excess hydraulic head h acting at its centre (an orthotropic soil is a soil whose material properties are different in all directions).
Let the coefficients of permeability in the coordinate directions x, y, and z be k x, k y, and k z, respectively. Consider the component of flow in the x direction.
The component of the hydraulic gradient, i x, at the centre of the element will be:
(2.9) 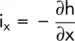
(Note that it is of negative sign as there is a head loss in the direction of flow).
The rate of change of the hydraulic gradient i xalong the length of the element in the x direction will be:
(2.10) 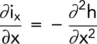
Hence, the gradient at the face of the element nearest the origin
(2.11) 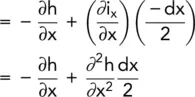
From Darcy's law:
(2.12) 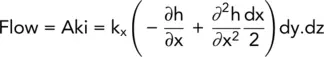
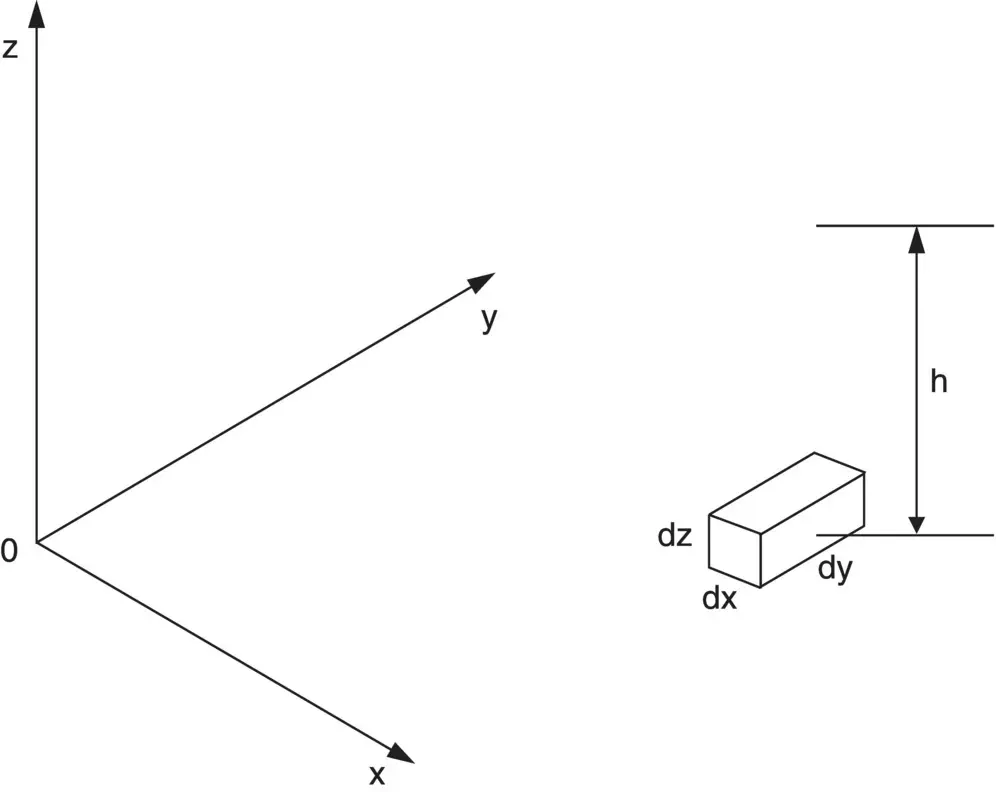
Fig. 2.7 Element in an orthotropic soil.
The gradient at the face furthest from the origin is:
(2.13) 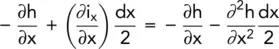
Therefore,
(2.14) 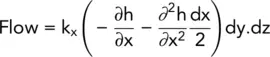
Equations (2.12)and (2.14)represent respectively the flow into and out of the element in the x direction, so that the net rate of increase of water within the element, i.e. the rate of change of the volume of the element, is (2.12)– (2.14).
Similar expressions may be obtained for flow in the y and z directions. The sum of the rates of change of volume in the three directions gives the rate of change of the total volume:
(2.15) 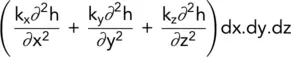
Under the laminar flow conditions that apply in seepage problems, there is no change in volume and the above expression must equal zero:
(2.16) 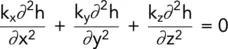
This is the general expression for three‐dimensional flow. In many seepage problems, the analysis can be carried out in two dimensions, the y term usually being taken as zero so that the expression becomes:
(2.17) 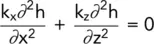
If the soil is isotropic, k x= k z= k and the expression is:
(2.18) 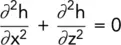
An isotropic soil is a soil whose material properties are the same in all directions.
It should be noted that these expressions only apply when the fluid flowing through the soil is incompressible. This is more or less the case in seepage problems when submerged soils are under consideration, but in partially saturated soils considerable volume changes may occur and the expressions are no longer valid.
2.9 Potential and stream functions
The Laplacian equation just derived can be expressed in terms of the two conjugate functions ϕ and 𝜓.
If we put
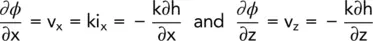
then

hence
(2.19) 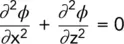
Also, if we put

then
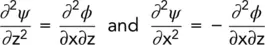
hence
(2.20) 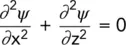
𝜙 and 𝜓 are known respectively as potential and stream functions. If 𝜙 is given a particular constant value then an equation of the form h = a constant can be derived (the equation of an equipotential line); if 𝜓 is given a particular constant value then the equation derived is that of a stream or flow line.
Direct integration of these expressions to obtain a solution is possible for straightforward cases. However, in general, such integration cannot be easily carried out and a solution obtained by a graphical method in which a flow net is drawn has been used by engineers for many decades. Nowadays, however, much use is made of computer software to find the solution using numerical techniques, such as the finite difference and finite element methods. Nevertheless, the method for drawing a flow net by hand is given in Section 2.10.3for readers interested in learning the techniques involved. The finite difference technique is described in Chapter 13where it is applied to the numerical determination of consolidation.
Читать дальше