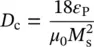(1.6) 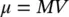
or by using the common notations (Caizer 2019)
(1.7) 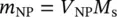
where m NPis the magnetic moment of the nanoparticle, V NPthe volume of the nanoparticle, and M sthe spontaneous magnetization of the magnetic material (the magnetization of a magnetic domain [ M ] corresponds to the spontaneous magnetization [or saturation]) ( M s) ( M ≡ M s). When the nanoparticle is spherically approximated, formula (1.7)is written as
(1.8) 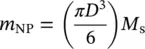
where D is the diameter of the nanoparticle, an approximation widely used both in theoretical calculations and in practical applications. From a magnetic point of view, it is important if the nanoparticle is spherical or has another shape, e.g. ellipsoidal, as the magnetic behavior in the external magnetic field may change a lot, especially due to soft magnetic materials case (see Section 1.1.5).
To conclude, it can be said that, from a magnetic point of view, in the case of bulk magnetic material, the base observable for the magnetic characterization is the magnetization given by relationship (1.4)or the elementary magnetic moment du, where the magnetization is nonuniform ( Figure 1.3a), whose field and space dependence must be known for the calculation of the integral.
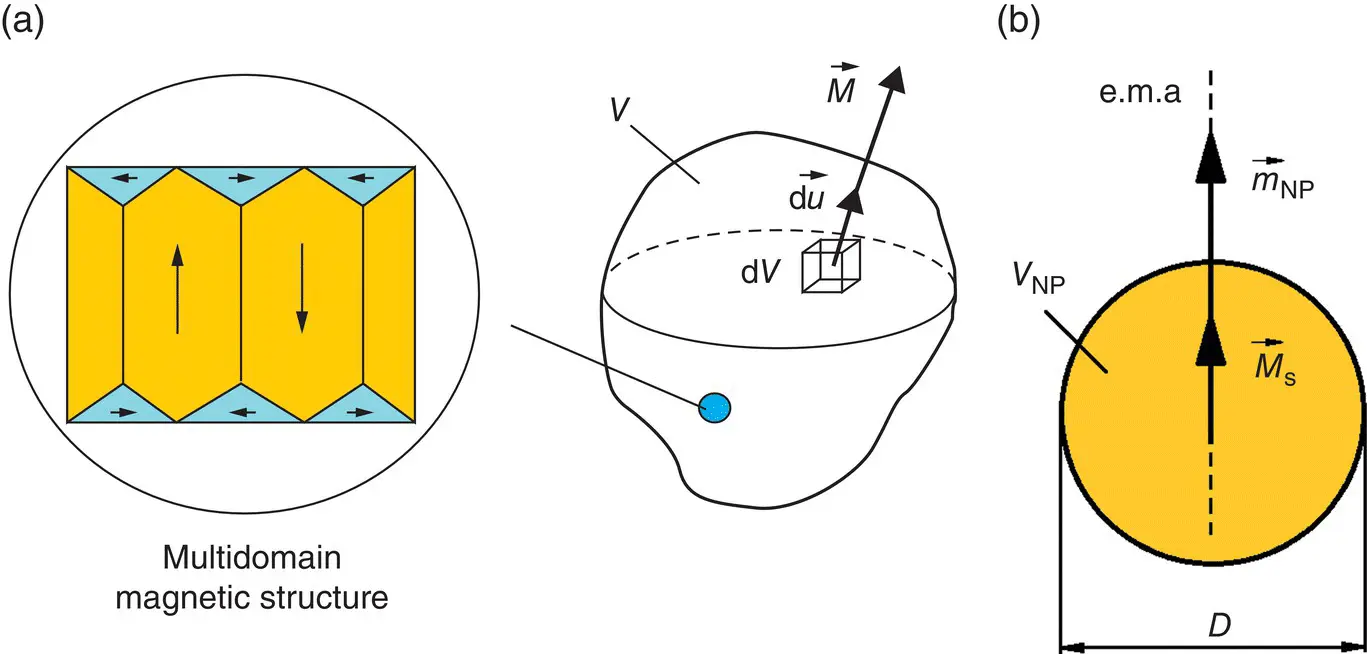
Figure 1.3 (a) Representation of the magnetization vectors ( 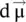 ) and elementary magnet moment (
) and elementary magnet moment ( 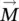 ) for an elementary volume d V of the bulk magnetic material of finite volume V , and an example of multidomain magnetic structures (in magnified image).
) for an elementary volume d V of the bulk magnetic material of finite volume V , and an example of multidomain magnetic structures (in magnified image).
Source: Caizer (2016). Reprinted by permission from Springer Nature;
(b) Spherical nanoparticle for uniaxial crystalline symmetry; e.m.a. is the easy magnetization axis.
Source: Caizer et al. (2020). Reprinted by permission from Springer Nature.
In the case of magnetic nanoparticles ( Figure 1.3b), the aspects are simplified, these being characterized by the magnetic moment of the nanoparticles given by Eq. (1.7)(or Eq. (1.8)for spherical nanoparticles), where M sis the spontaneous magnetization of the nanoparticle material which is a known observable ( M sis a material parameter), and V NPis the effective volume of the nanoparticle. V NPand in most theoretical or practical cases can be easily approximated by the volume of a sphere, ellipsoid of revolute or flattened, cylinder, etc., which radically simplifies the calculations. However, for this reason, the exact given situation will have to be taken into account, in order not to introduce errors.
1.1.3 Magnetic Structures
The bulk ferromagnetic magnetic material consists of magnetic domains (Kneller 1962) spontaneously magnetized to saturation, resulting from the balance of exchange forces, which tend to align the atomic (ionic) magnetic moments in the network, and magnetostatic forces, which, through the created magnetic poles, tend to disorient the magnetic moments from their parallel alignment. The magnetic structure is stable when there is a balance between the exchange and magnetostatic forces, respectively, in the condition of minimum magnetocrystalline energy. Experimentally, different structures of magnetic domains were observed, the most common being those with free magnetic poles ( Figure 1.4a) and magnetic structures without free magnetic poles (with magnetic flux closing domains) ( Figure 1.4b). The first magnetic structure is characteristic of uniaxial crystals and the second magnetic structure is characteristic of the magnetic crystals with cubic symmetry.
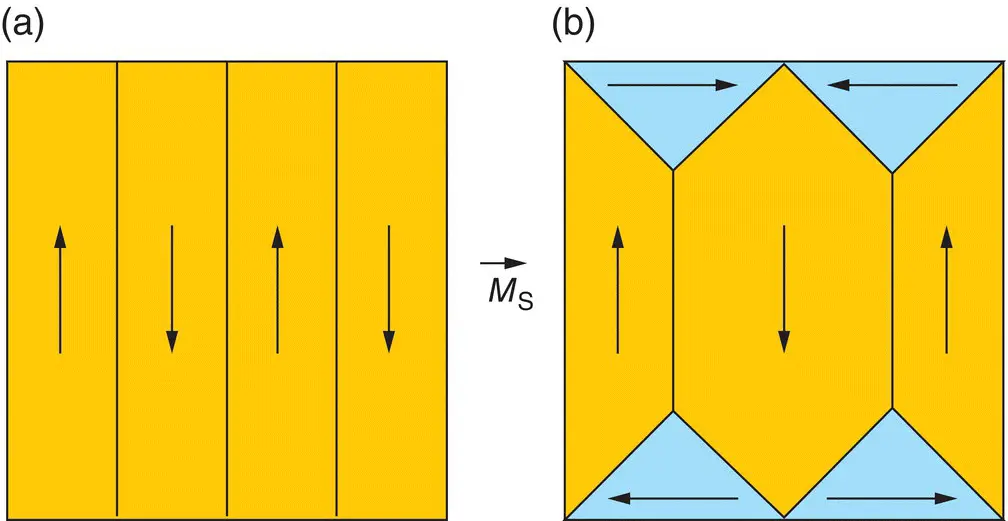
Figure 1.4 Magnetic structures of nanoparticles: multidomain nanoparticles with (a) uniaxial and (b) cubic symmetry.
Source: Caizer et al. (2017). Reprinted by permission from Springer Nature.
The magnetic domains are separated from each other by narrow regions in the crystal (transition) called walls of magnetic domains. Within the walls is a continuous change in orientation of spins, from the direction of magnetization in one domain to the direction of magnetization in the neighboring domain. The most common walls found in magnetic structures are the Bloch‐type walls (Bloch 1930) or 180 walls, which separate 2 neighboring domains with opposite magnetizations. They are also the most stable in magnetic structures. But there are also Nèel or 90's walls, which separate adjacent domains, where the magnetizations in the domains are oriented at 90°. Nèel‐type walls are generally unstable.
The magnetic domains are magnetized uniformly (at saturation), characterized by the spontaneous magnetization of M s. In the closing domains, the spontaneous magnetization is oriented at 45 in relation to the direction of separation of the domains ( Figure 1.4b) so that the normal component of the magnetization is continuous along the boundaries separating the domains, and, thus, no magnetostatic energy will occur.
The thickness of the domain walls is generally less than 10 5A, and that of the walls in the range 10–10 3A, strongly depending on the anisotropy of the material and the exchange forces.
When the volume of the magnetic material is reduced in the nanometer range, the magnetic structure changes radically, reaching a unidominal structure, under a certain critical volume ( V cr) (Kittel 1946). Schematically, this aspect is shown in Figure 1.5, in the case of the spherical nanoparticle (Caizer 2004a). Above the critical volume ( V > V cr), the nanoparticle has an incipient structure of magnetic domains, which depending on the crystalline symmetry of the material, can be of the form: (a) case of uniaxial symmetry or (b) case of cubic symmetry.
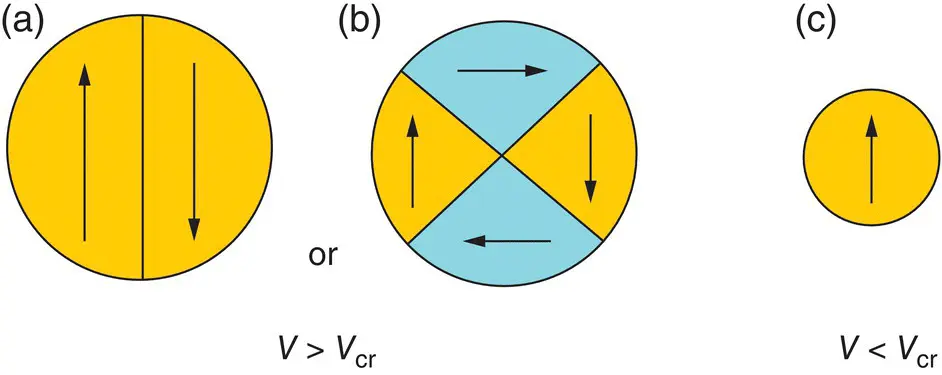
Figure 1.5 Multidomain magnetic nanoparticles with (a) uniform magnetization (uniaxial symmetry) and (b) nonuniform magnetization (cubic symmetry), and (c) single‐domain nanoparticle.
Source: Adapted from Caizer and Stefanescu (2003).
Using the classic model of the single‐domain particle, it can estimate the critical diameter D c(or the critical volume V cr) at which the transition from the state with the structure of magnetic domains (multidomains) to the one with the single‐domain structure takes place. Thus, for the critical diameter, the following formula is obtained:
(1.9) 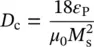
Читать дальше

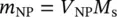
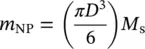

 ) and elementary magnet moment (
) and elementary magnet moment ( 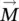 ) for an elementary volume d V of the bulk magnetic material of finite volume V , and an example of multidomain magnetic structures (in magnified image).
) for an elementary volume d V of the bulk magnetic material of finite volume V , and an example of multidomain magnetic structures (in magnified image).