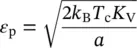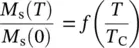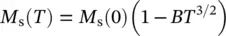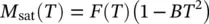Magnetic Nanoparticles in Human Health and Medicine

where ε Pis the energy density of the domain wall, μ 0is the magnetic permeability of the vacuum ( μ 0= 4π × 10 −7H m −1), and M sthe spontaneous magnetization of the material.

The energy density of the wall was determined by Landau–Lifschtz, finding the following formula:

(1.10)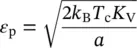

where D is the constant in the crystalline network, T Cis the Curie temperature of the magnetic material, K Vis the constant magnetoscrystalline anisotropy, and K Bis the Boltzmann constant.

The critical diameter at which the transition from the multidomains structure to the single‐domain structure takes place depending a lot on the magnetic anisotropy of the nanoparticle. For Co, the value of ~60 nm was found (…). However, in the case of Ni–Zn ferrite nanoparticles, Caizer finds a value D c= 21.6 nm, for the energy of the domain wall ε Pof 0.145 erg cm −2(Caizer 2003a).

In conclusion, when conducting theoretical and practical studies on the use of nanoparticles, it is very important to know the critical diameter ( D c) under which the nanoparticle becomes one with a single‐magnetic structure, for which a previous evaluation is needed.

Another important aspect to consider, when a magnetic material is reduced to the nanoscale, is the saturation magnetization of the material, which is influenced by such reduction.

In the case of bulk magnetic material, the saturation magnetization ( M sat) (theoretically obtained in intense magnetic field and at low temperatures) is equal to the spontaneous magnetization ( M s), being a known parameter of material. Example, in the case of Fe, the saturation magnetization at room temperature is 1714 kA m −1(Cullity and Graham 2009), and in the case of Fe 3O 4, it is 477.5 kA m −1(Smit and Wijin 1961). The spontaneous magnetization of the bulk magnetic material decreases with temperature, having the maximum value at 0 K ( M s(0)) and zero at a temperature, generally high (hundreds of degrees), which is Curie temperature in the case of ferromagnetics and Nèel temperature in the case of ferrimagnetic materials. The temperature variation of the spontaneous magnetization of massive ferromagnetic material, such as Fe, Co, and Ni ( Figure 1.6a), is a universal function that does not involve indeterminate constants:

(1.11)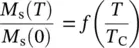

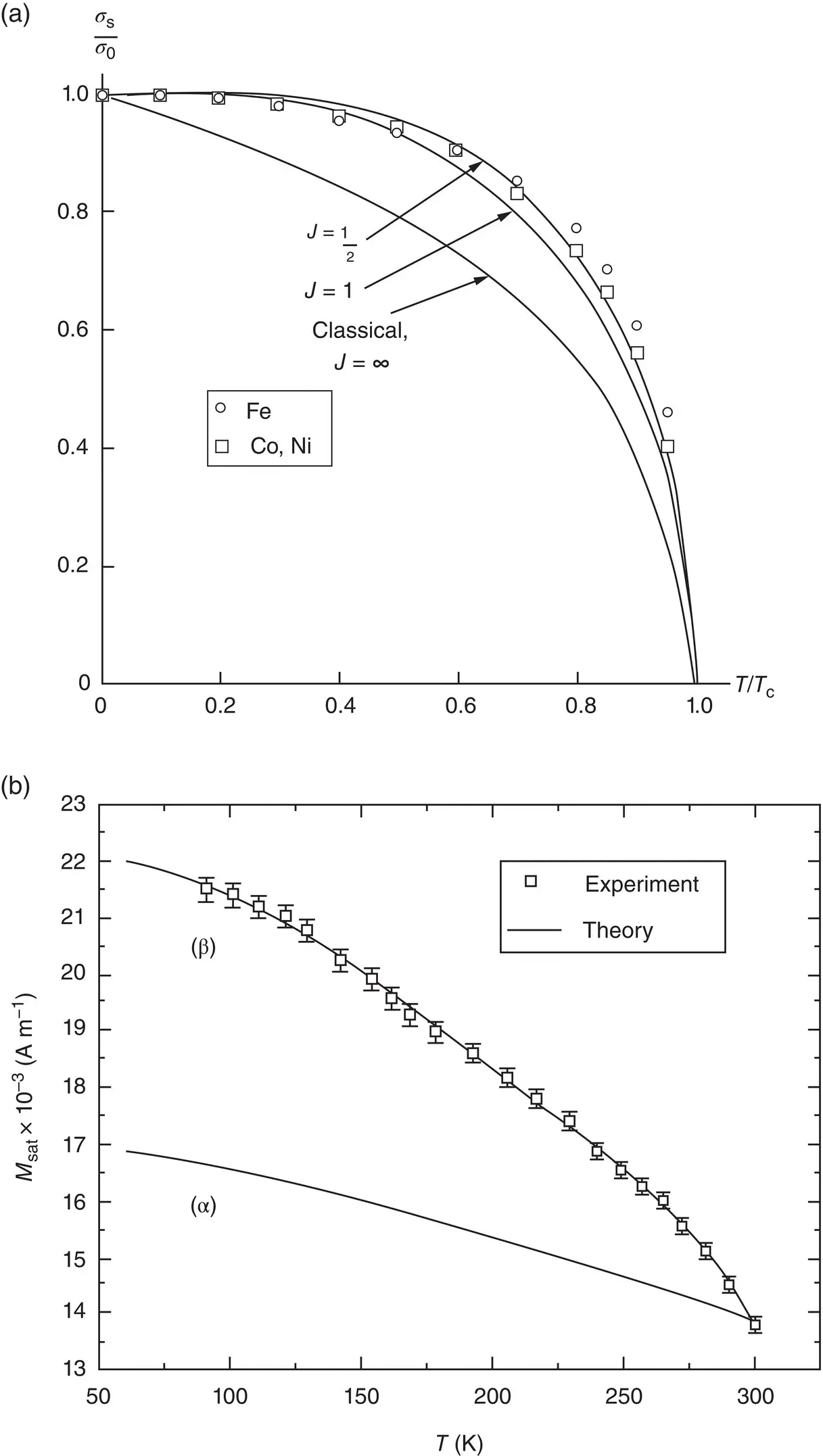
Figure 1.6 (a) Relative saturation magnetization of iron, cobalt, and nickel as a function of relative temperature. Calculated curves are shown for three values of J .

Source: Cullity and Graham (2009). Reproduced with permission from John Wiley & Sons;

(b) Curves that represent the dependence of the saturation magnetization on temperature according to Eq. (1.12)(curve α ) and Eqs. (1.13)and (1.14)(curve β ); experimental curve (□).

Source: Caizer (2005a). Reproduced with permission from Springer Nature.

At low temperatures, this variation is well described by Bloch's law (law in T 3/2(Bloch 1930), deduced from the spin wave model,

(1.12)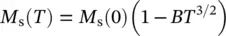

which is the exact solution of the Hamiltonian Heisemberg at low temperatures. In Eq. (1.12), B is a constant whose value depends on the exchange integral.

This dependence is well verified experimentally both for bulk ferromagnetic materials (Fe, Ni) (Aldred and Frohle 1972; Aldred 1975) and for some bulk spinel ferrites, such as Mn xFe 3 − xO 4ferrite for 0.2 < x < 1.0 (Dillon 1962).

However, when the magnetic material has nanometric sizes, such as nanoparticles, some theoretical calculations and some experimental results have shown that the temperature exponent is greater than the value 3/2, corresponding to the bulk material (Hendriksen et al. 1992, 1993; Linderoth et al. 1993). Thus, Morais et al. (2000) showed that, depending on the temperature of the saturation magnetization in the range 4.2–293 K, in the case of a ferrofluid with NiFe 2O 4nanoparticles having an average diameter of 11.1 nm, it deviates from the law corresponding to the bulk material. In the case of magnetite (Fe 3O 4) nanoparticles coated with oleic acid, Caizer (2003b) shows that the law is well verified for T 2instead of T 3/2, and the constant of M s(0) in Eq. (1.12)becomes in this case a function of temperature:

(1.13)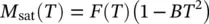

However, in the case of Mn 0.6Fe 2.4O 4nanoparticles coated with oleic acid (Caizer 2005a), it is found that is verified in the law of Eq. (1.12), but M s(0) is no longer a constant but is temperature‐dependent according to the formula:

(1.14)

In this equation, n is the concentration of the nanoparticles, and c iare constants whose value is known, resulting from the fitting of the experimental data. In Figure 1.6b is shown the dependence on M sat− T in this case, where the deviation is highlighted: ( α ) is the curve for bulk and ( β ) is the curve for nanoparticles. These results as well as others (Caizer 2002) show that T 3/2valid in the case of bulk magnetic material is no longer verified in the case of magnetic nanoparticles, and there are different interpretations for this.

Another important aspect in the case of nanoparticles is the fact that the saturation magnetization measured experimentally at room temperature is lower than that corresponding to the same bulk magnetic material (Berkowitz et al. 1975; Zhang et al. 1997; Kodama 1999; Caizer and Stefanescu 2002; Caizer 2003b). It has also been found experimentally that the decrease in saturation magnetization is all the more pronounced the smaller the nanoparticles, a few nm. In Figure 1.7is shown the dependency of saturation magnetization as a function of the average nanoparticle diameter in the case of Ni 0.35Zn 0.65Fe 2O 4nanoparticles (Caizer and Stefanescu 2002). Also, a similar dependency is shown in Figure 1.12b for the magnetic moment of the nanoparticles (Wu et al. 2017).

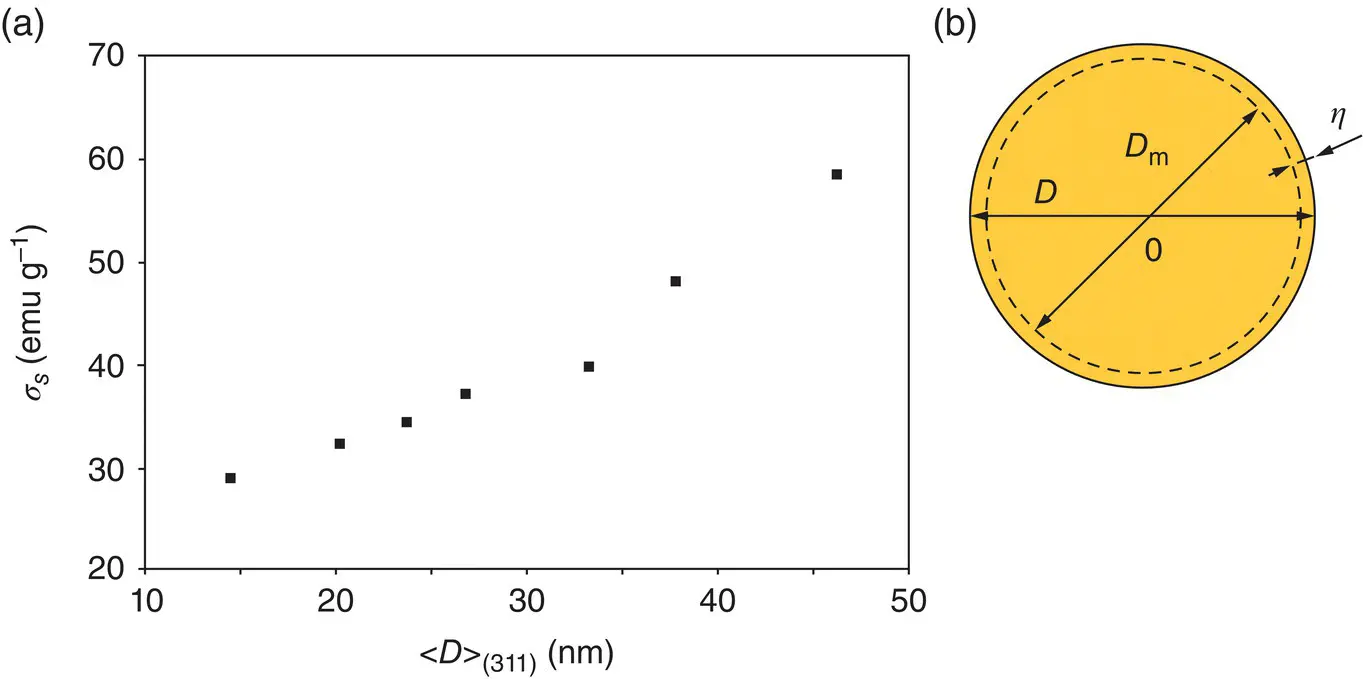
Figure 1.7 (a) Specific saturation magnetization as a function of the mean diameter of nanocrystallites.

Source: Caizer and Stefanescu (2002). Reprinted by permission from IOP Publishing.

(b) Core‐shell pattern of the spherical nanoparticle.

Source: Caizer (2016). Springer Nature.

In Ref. (Caizer 2016) is presented in more detail the aspects that lead to the decrease of the saturation magnetization of the nanoparticles, considering the core‐shell model in which there is a layer on the surface of the nanoparticles where the magnetic moments are no longer aligned as in the ordered magnetic core. As a result, in the case of nanoparticles, a magnetic diameter ( D m) determined by the nanoparticle core in which the spins are magnetically aligned must be considered, which is generally smaller than the physical diameter ( D ) of the nanoparticles: D m< D . Difference ( D − D m) becomes even more pronounced in the case of ferrimagnetic nanoparticles (Berkowitz et al. 1975, 1980; Kodama et al. 1996), surfactated (Caizer 2002) or in SiO 2matrix, this reaching even up to 2–3 nm (Caizer et al. 2003; Caizer 2008).