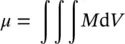Table 1.1 Magnetic susceptibility values for different bulk magnetic materials.
| Type of magnetic material |
Diamagnetic |
Paramagnetic |
Ferromagnetic |
| χ |
−(10 −4– 10 −6) ( χ < 0) |
10 −3– 10 −5( χ > 0) |
10 2– 10 5( χ ≫ 0) |
When the size of the magnetic material, ferro‐ or ferrimagnetic, is reduced to the range of nm – tens of nm, it was found that the magnetic properties specific to the bulk change radically, regardless of the type of magnetic ordering (Caizer 2016). Thus, in the category of magnetic materials with magnetic ordering of ferromagnetic or ferrimagnetic type, a special category appears called superparamagnetic materials. This name was introduced by Bean (Bean and Livingston 1959) in order to distinguish this material from the bulk basic magnetic ones: paramagnetic and ferromagnetic/ferrimagnetic. This is because the material itself is ordered magnetically, ferro‐ or ferrimagnetic, but behaves in the external magnetic field like a paramagnetic material. This name was introduced considering that, at the microstructural level, we do not have individual atoms with magnetic moment isolated from each other, as in the case of paramagnetics, but a magnetic structure (magnetic domain) that contains a very large number of atoms with magnetic moments (even more greater than 10 5) coupled to each other (with magnetic ordering) as a result of the exchange or superexchange interaction. Superparamagnetic behavior is characteristic of magnetic materials with small sizes in the nanometers range, depending on the nature of the material.
In biomedical applications, the most used materials are those with magnetic ordering of ferrimagnetic or even ferromagnetic type because they present an intense magnetism and fast response to an external magnetic field. However, the most used in applications and much studied today in research for various applications are materials based on iron oxides (ferrimagnetic) (Smit and Wijin 1961) with the magnetite (Fe 3O 4) typical representative ( Figure 1.2). Magnetite is an inverse spinel (Fe 2+Fe 2 3+O 4 2−) with a cubic structure in which the magnetic cations of Fe 2+and Fe 3+are found in two magnetic subllatices A (tetrahedral) and B (octahedral) having opposite magnetizations: Fe 3+[Fe 2+Fe 3+] O 4 2, where the right parenthesis represents the ions from the sublatice B and Fe 3+, from outside, the parenthesis represents the ions from the sublatice A. However, recent experiments (Garcia and Subias 2004) have shown a difference in the electric charge of Fe(B) ions, where Fe 2.5+is present, as shown in Figure 1.2(Parkinson et al. 2012).
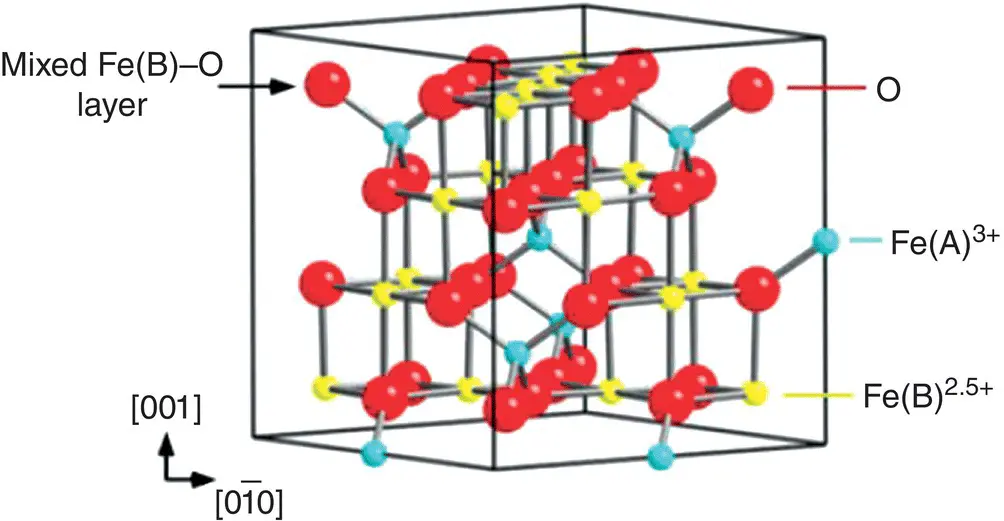
Figure 1.2 Fe 3O 4bulk unit cell (inverse spinel structure).
Source: Parkinson et al. (2012). CC BY 3.0.
The basic magnetic aspects of bulk magnetic material, ferromagnetic, or ferrimagnetic, and how they change in the case of nanomaterial, will be presented below considering the magnetic particles/nanoparticles for biomedical applications.
1.1.2 The Atomic Magnetic Moment, Magnetization, and Magnetic Moment of the Nanoparticle
In the case of a bulk paramagnetic, ferro‐, or ferrimagnetic material, the magnetism is due to the existence of the magnetic moment (total) at the atomic (or ionic/molecular) level (Kneller 1962; Jacobs and Bean 1963; Vonsovskii 1974; Caizer 2004a):
(1.1) 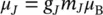
as a result of the spin–orbit coupling (vector summation of the spin magnetic moments (total) (  ) and the orbital magnetic moments (total) (
) and the orbital magnetic moments (total) ( 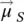 ): the vector model of the atom (
): the vector model of the atom ( 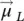 =
=  +
+ 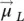 ). In Eq. (1.1), g Jis the spectroscopic splitting factor (Lande factor) at the atomic level,
). In Eq. (1.1), g Jis the spectroscopic splitting factor (Lande factor) at the atomic level,
(1.2) 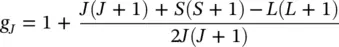
m Jis the internal magnetic quantum number (total), which can take (2 J + 1) values (according to quantum physics, respectively – J , …, 0, …, + J ), and μ Bis the Bohr magnetone:
(1.3) 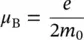
with the observables: e is the electron charge ( e = 1.6 × 10 −19C), m 0is the resting electron mass ( m 0= 9.1 × 10 −31kg), and h is the Planck constant ( h = 6.63 × 10 −34Js). In Eq. (1.2), L is the internal orbital quantum number (total), and S is the internal spin quantum number.
Macroscopically, the quantity that characterizes the bulk magnetic material, from a magnetic point of view, is the magnetization ( 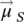 ), defined as a numerical quantity equal to the resulting magnetic moment (
), defined as a numerical quantity equal to the resulting magnetic moment ( 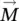 ,
, 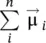 being the total magnetic moment of the atom/ion ( Eq. 1.1), and i the number of atoms/ions in volume V ) of the volume unit (Caizer 2004a),
being the total magnetic moment of the atom/ion ( Eq. 1.1), and i the number of atoms/ions in volume V ) of the volume unit (Caizer 2004a),
(1.4) 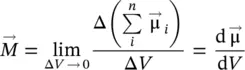
respectively, in the hypothesis of a continuous environment. According to formula (1.4), the magnetization vector 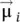 has the same direction and sense as the elementary magnetic moment vector
has the same direction and sense as the elementary magnetic moment vector 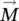 .
.
In accordance with Eq. (1.4), the magnetic moment of a volume of magnetic material will be
(1.5) 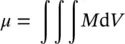
In the case of reducing the volume of ferrous‐ or ferrimagnetic material in the nanometer range (nm – tens of nm), as in the case of magnetic nanoparticles, when there is a single magnetic domain (Weiss domain) (or in the case of a nanoparticle volume even smaller than the one corresponding to a magnetic domain), the magnetization ( M ) is uniform in the finite volume of material. Thus, in this case, of the single‐domain magnetic nanoparticle, the resulting magnetic moment can be written as (Caizer 2016)
Читать дальше


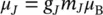
 ) and the orbital magnetic moments (total) (
) and the orbital magnetic moments (total) ( 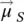 ): the vector model of the atom (
): the vector model of the atom ( 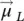 =
=  +
+ 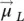 ). In Eq. (1.1), g Jis the spectroscopic splitting factor (Lande factor) at the atomic level,
). In Eq. (1.1), g Jis the spectroscopic splitting factor (Lande factor) at the atomic level,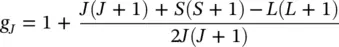
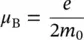
 ), defined as a numerical quantity equal to the resulting magnetic moment (
), defined as a numerical quantity equal to the resulting magnetic moment (  ,
, 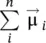 being the total magnetic moment of the atom/ion ( Eq. 1.1), and i the number of atoms/ions in volume V ) of the volume unit (Caizer 2004a),
being the total magnetic moment of the atom/ion ( Eq. 1.1), and i the number of atoms/ions in volume V ) of the volume unit (Caizer 2004a),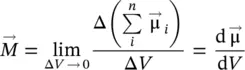
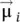 has the same direction and sense as the elementary magnetic moment vector
has the same direction and sense as the elementary magnetic moment vector 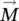 .
.