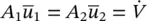As a fluid moves past a solid boundary or wall, the velocity of the fluid particles at the wall must equal the velocity of the wall; the relative velocity between the fluid and the wall at the surface of the wall is zero, which is called the no‐slip condition, and results in a varying magnitude of the flow velocity (e.g. a velocity gradient), as one moves away from the wall (see Figure 1.7).
There are two types of viscosities, namely, dynamic viscosity , which is the ratio of a shear stress to a fluid strain (velocity gradient), and kinematic viscosity , which is defined as the ratio of dynamic viscosity to density.
The dynamic viscosity, based on a two‐dimensional boundary layer flow and the velocity gradient d u /d y occurring in the direction normal to the flow, as shown in Figure 1.7, leading to the shear stress within a fluid being proportional to the spatial rate of change of fluid strain normal to the flow, is expressed as
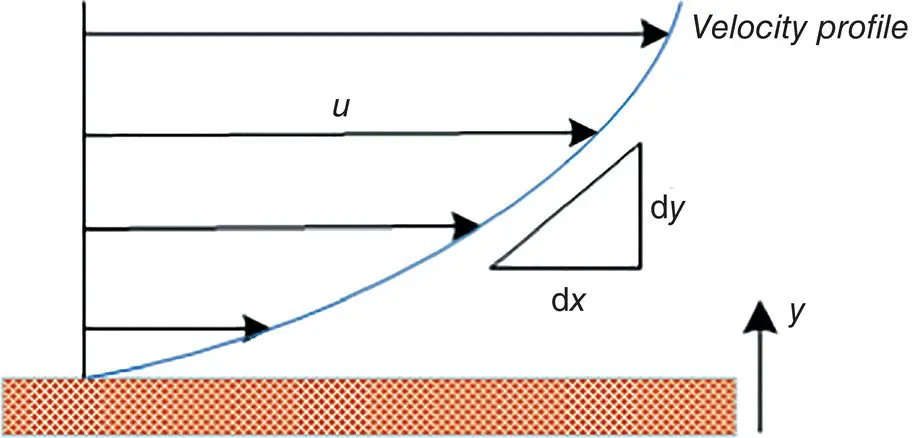
Figure 1.7 Schematic diagram of velocity profile moving away from a wall (i.e. as y increases).
(1.44) 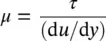
where the units of μ are Ns/m 2or kg/ms in the SI system and lb fs/ft 2in the English system.
The kinematic viscosity then becomes
(1.45) 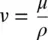
where the units of ν are m 2/s in the SI system and ft 2/s in the English system.
From the viscosity perspective, the types of fluids may be classified into the two groups that follow below.
These fluids have a dynamic viscosity dependent upon temperature and pressure and independent of the magnitude of the velocity gradient. For such fluids, Eq. (1.44)is applicable. Some examples are water and air.
Fluids that cannot be represented by Eq. (1.44)are called non‐Newtonian fluids . These fluids are very common in practice and have a more complex viscous behavior due to the deviation from Newtonian behavior. There are several approximate expressions to represent their viscous behavior. Some examples of such fluids are slurries, polymer solutions, oil paints, toothpaste, and sludges.
The basic equations of fluid flow may be derived from important fundamental principles, namely, conservation of mass, conservation of momentum (i.e. Newton's second law of motion), and conservation of energy. Although general statements of these laws can be written (applicable to all substances, e.g. solids and fluids), in fluid flow these principles can be formulated as a function of flow parameters, namely, pressure, temperature, and density. The equations of motion may be classified into two general types: the equations of motion for inviscid fluids (i.e. frictionless fluids) and the equations of motion for viscous fluids. In this regard, we deal with the Bernoulli equations and Navier–Stokes equations.
The continuity equation is based on the conservation of mass principle. The requirement that mass be conserved at every point in a flowing fluid imposes certain restrictions on the velocity u and density ρ . Therefore, the rate of mass change is zero, so that for a steady flow, the mass of fluid in the control volume remains constant, and therefore the mass of fluid entering per unit time is equal to the mass of fluid exiting per unit time. We now apply this idea to a steady flow in a stream tube ( Figure 1.8). The continuity equation for the flow of a compressible fluid through a stream tube is

Figure 1.8 Fluid flow in a stream tube.
(1.46) 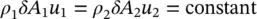
where ρ 1 δA 1 u 1is the mass entering per unit time (at section 1) and ρ 2 δA 2 u 2is the mass exiting per unit time (at section 2).
In practice, for the flow of a real fluid through a pipe or a conduit, the mean velocity is used since the velocity varies from wall to wall. Then, Eq. (1.46)can be rewritten as
(1.47) 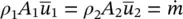
where 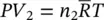 and
and 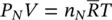 are the mean velocities at sections 1 and 2.
are the mean velocities at sections 1 and 2.
For fluids that are considered as incompressible, Eq. (1.47)is simplified to the following, since ρ 1= ρ 2:
(1.48) 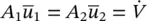
The various forms of the continuity equation for steady‐state and unsteady‐state cases are summarized below:
The steady‐state continuity equation for an incompressible fluid in a stream tube:(1.49)
The unsteady‐state continuity equation for an incompressible fluid in a stream tube:(1.50)
The steady‐state continuity equation for an incompressible fluid in cartesian coordinates:(1.51)
The unsteady‐state continuity equation for an incompressible fluid in cartesian coordinates:(1.52)
The steady‐state continuity equation for an incompressible fluid in cylindrical coordinates:(1.53)
The steady‐state continuity equation for a compressible fluid in a stream tube:(1.54)
The steady‐state continuity equation for a compressible fluid in cartesian coordinates:(1.55)
The steady‐state continuity equation for a compressible fluid in cylindrical coordinates:(1.56)
The unsteady‐state continuity equation for a compressible fluid in a stream tube:(1.57)
The unsteady‐state continuity equation for a compressible fluid in cartesian coordinates:(1.58)
The unsteady‐state continuity equation for a compressible fluid in cylindrical coordinates:(1.59)
The analysis of fluid‐flow phenomena is fundamentally dependent on the application of Newton's second law of motion, which is more general than the momentum principle, stating that when the net external force acting on a system is zero, the linear momentum of the system in the direction of the force is conserved in both magnitude and direction (the so‐called conservation of linear momentum ). In fact, the momentum principle is concerned only with external forces, and provides useful results in many situations without requiring much information on the internal processes within the fluid. The momentum principle finds applications in various types of flows (e.g. steady or unsteady, compressible or incompressible).
Читать дальше


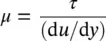
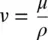

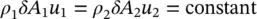
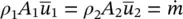
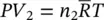 and
and 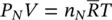 are the mean velocities at sections 1 and 2.
are the mean velocities at sections 1 and 2.