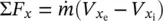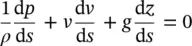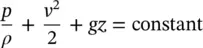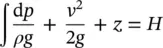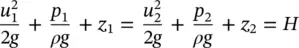The motion of a particle must be described relative to an inertial coordinate frame. The one‐dimensional momentum equation at constant velocity can be written as follows:
(1.60) 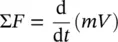
where ∑ F stands for the sum of the external forces acting on the fluid, and mV stands for the kinetic momentum in that direction. Equation (1.60)states that the time rate of change of the linear momentum of the system in the direction of V equals the resultant of all forces acting on the system in the direction of V . The linear momentum equation is a vector equation and is therefore dependent on a set of coordinate directions.
The rate of change of momentum of a control mass can be related to the rate of change of momentum of a control volume via the continuity equation. Then, Eq. (1.60)becomes
(1.61) 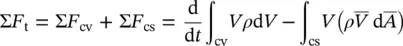
Here, the sum of forces acting on the control volume in any direction is equal to the rate of change of momentum of the control volume in that direction plus the net rate of momentum flux from the control volume through its control surface in the same direction.
For a steady flow, if the velocity across the control surface is constant, the momentum equation in scalar form becomes
(1.62) 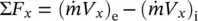
If the mass flow rate 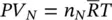 is constant, Eq. (1.62)can be written as
is constant, Eq. (1.62)can be written as
(1.63) 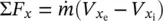
Similar expressions can be written for the y and z directions.
Euler's equation is a mathematical statement of Newton's second law of motion, and finds application in an inviscid fluid continuum. This equation states that the product of mass and acceleration of a fluid particle can be equated vectorially with the external forces acting on the particle. Consider a stream tube, as shown in Figure 1.9, with a cross‐sectional area small enough for the velocity to be considered constant along the tube.
The following is a simple form of Euler's equation for a steady flow along a stream tube, representing the relationship in differential form between pressure p , velocity v , density ρ , and elevation z , respectively:
(1.64) 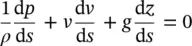
For an incompressible fluid ( ρ is constant), the integration of the above equation gives the following expression along the streamline (with respect to s ) for an inviscid fluid:
(1.65) 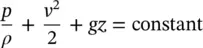
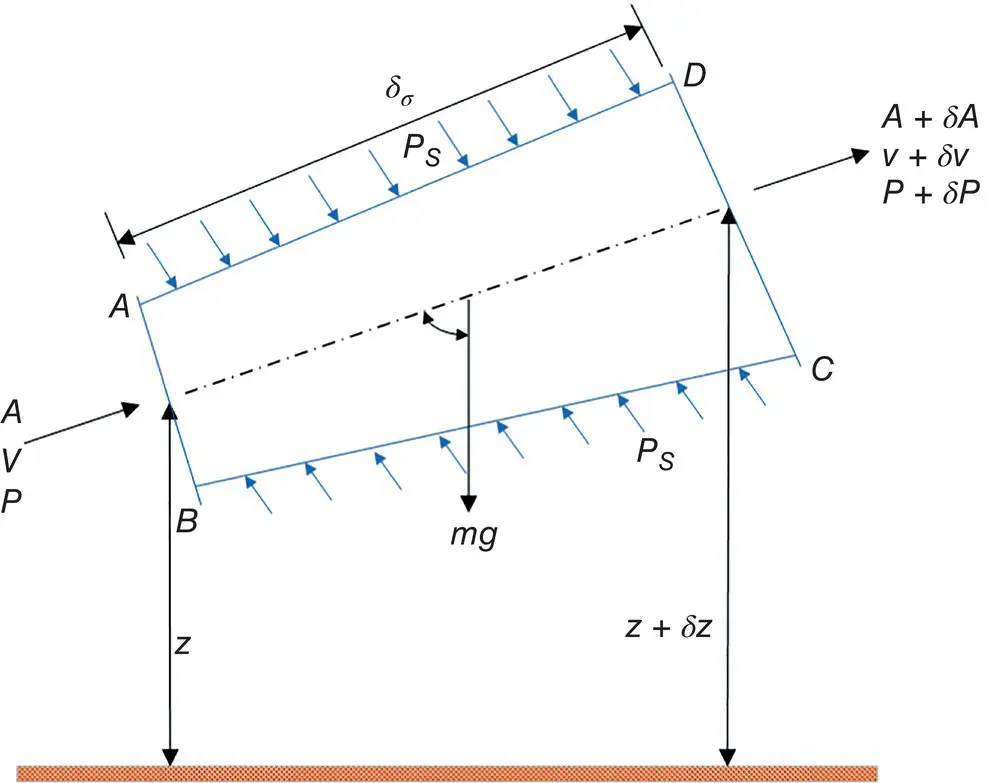
Figure 1.9 Relationship between velocity, pressure, elevation, and density for a stream tube.
For a compressible fluid, the integration of Eq. (1.64)can only be completed to provide the following:
(1.66) 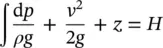
Note that the relationship between 𝜌 and p needs to be known for the given case, and that for gases the relationship can be in the form p 𝜌 n= constant, varying from adiabatic to isothermal conditions, while for a liquid, 𝜌 (d p /d 𝜌 ) = K , which is an adiabatic modulus.
This equation can be written for both incompressible and compressible flows. Under certain flow conditions, Bernoulli's equation for incompressible flow is often referred to as a mechanical‐energy equation because of the fact that it is similar to the steady‐flow energy equation obtained from the FLT for an inviscid fluid with no external heat transfer and no external work. It is necessary to point out that for inviscid fluids, viscous forces and surface tension forces are not taken into consideration, leading to negligible viscous effects. The Bernoulli equation is commonly used in a variety of practical applications, particularly in flows in which the losses are negligibly small, for example, in hydraulic systems. The following is the general Bernoulli equation per unit mass for inviscid fluids between any two points:
(1.67) 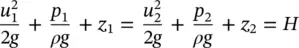
Here, each term has a dimension of a length or head scale. In this regard, u 2/2 g (kinetic energy per unit mass) is referred to as the velocity head, p / 𝜌 g (pressure energy per unit mass) as the pressure head , z (potential energy per unit mass) as the potential head (constant total head), and H (total energy per unit mass) as the total head in meters. Subscripts 1 and 2 denote where the variables are evaluated on the streamline.
The terms in Eq. (1.67)represent energy per unit mass and have the unit of length. Bernoulli's equation can be obtained by dividing each term in Eq. (1.65)by g . These terms, both individually and collectively, indicate the quantities that may be directly converted to produce mechanical energy.
In summary, if we compare Eq. (1.67)with the general energy equation, we see that the Bernoulli equation contains even more restrictions than might first be realized, due to the following main assumptions:
steady flow (common assumption applicable to many flows);
incompressible flow (acceptable if the Mach number is less than 0.3);
frictionless flow along a single streamline (highly restrictive);
no external shaft work or heat transfer occurs between 1 and 2.
(e) Navier–Stokes Equations
The Navier–Stokes equations are the differential expressions of Newton's second law of motion, and are known as constitutive equations for viscous fluids. These equations were named after C.L.M.H. Navier and Sir G.G. Stokes, who are credited with their derivation.
For viscous fluids, two force aspects, namely, a body force and a pressure force on their surface, are taken into consideration. The solution of these equations is dependent upon what flow information is known. The solutions evolving now for such problems have become extremely useful. Recently numerical software packages have been developed in the field of fluid flow for many engineering applications.
Читать дальше

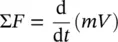
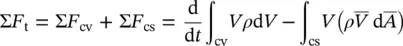
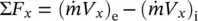
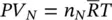 is constant, Eq. (1.62)can be written as
is constant, Eq. (1.62)can be written as