Ibrahim Dincer - Thermal Energy Storage Systems and Applications

Exergy efficiency permits a better matching of energy sources and uses, leading to high‐quality energy being reserved for performing high‐quality tasks and not used for low‐quality end uses.

For a good understanding of the operation of TES systems and their components, as well as the behavior of fluid flows, an extensive background on fluid mechanics is essential. In addition to learning the principles of fluid flow, the student and/or engineer should develop an understanding of the properties of fluids and be able to solve practical thermodynamic problems.

In practice, engineers are regularly faced with a large variety of fluid‐flow problems:

subcooled liquids, like water and brine;

mixtures of boiling liquids and the ensuing vapor;

mixtures of refrigerants and absorbents;

mixtures of air and water vapor as humid air; and

low‐ and high‐pressure gases.

To deal effectively with fluid‐flow systems, it is necessary to identify flow categories, defined in predominantly mathematical terms, that allow the appropriate analysis to be undertaken by identifying suitable and acceptable simplifications. Examples of the categories to be introduced include variation of the flow parameters with time (steady or unsteady) or variations along the flow path (uniform or nonuniform). Similarly, compressibility effects may be important in high‐speed gas flows, but may be ignored in many liquid flow situations.

Various criteria allow fluid flows to be classified into the following categories:

uniform or nonuniform,

one‐, two‐, or three‐dimensional,

steady‐ or unsteady‐state,

laminar or turbulent, and

compressible or incompressible.

Also, liquids flowing in open channels may be classified according to their regions, for example, subcritical, critical, or supercritical, and gas flows may be categorized as subsonic, transonic, supersonic, or hypersonic.

If the velocity and cross‐sectional area are constant in the direction of flow, the flow is uniform. Otherwise, the flow is nonuniform.

The flow of real fluids occurs in three dimensions. However, in the analysis, the conditions are often simplified to either one‐ or two‐dimensional, depending on the flow problem under consideration. If all fluid and flow parameters (velocity, pressure, elevation, temperature, density, viscosity, etc.) are considered to be uniform throughout any cross‐section and vary only along the direction of flow ( Figure 1.6a), the flow is one‐dimensional. Two‐dimensional flow occurs when the fluid and flow parameters have spatial gradients in two directions, that is, x and y axes ( Figure 1.6b). In three‐dimensional flow, the fluid and flow parameters vary in three directions, that is, x , y , and z axes, and the gradients of the parameters occur in all three directions.

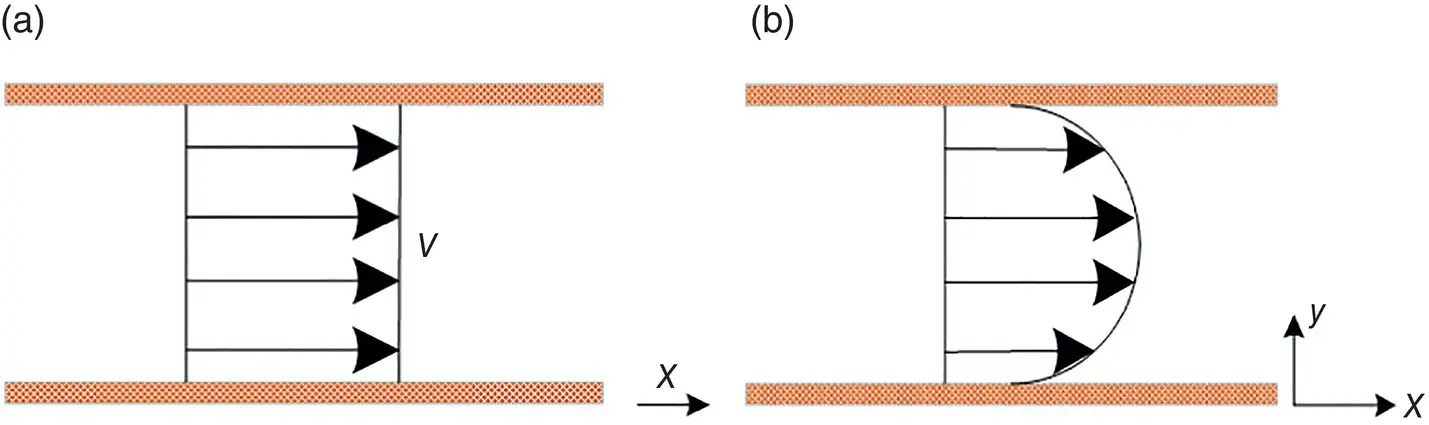
Figure 1.6 Velocity profiles for flows: (a) one‐dimensional flow, (b) two‐dimensional flow.

Steady flow is defined as a flow in which the flow conditions do not change with time. However, we may have a steady flow in which the velocity, pressure, and cross‐section of the flow vary from point to point but do not change with time. This requires us to distinguish by dividing such a flow into steady , uniform flow and steady , nonuniform flow . In a steady, uniform flow, all conditions (e.g. velocity, pressure, and cross‐sectional area) are uniform and do not vary with time or position. For example, uniform flow of water in a duct of constant cross‐section is considered a steady, uniform flow. If the conditions (e.g. velocity and cross‐sectional area) change from point to point (e.g. from cross‐section to cross‐section) but not with time, we have a steady, nonuniform flow. For example, a liquid flows at a constant rate through a tapering pipe running completely full.

If the conditions vary with time, the flow becomes unsteady. If at a given time the velocity at every point in the flow field is the same, but the velocity changes with time, we have an unsteady , uniform flow . An example is an accelerating flow of a fluid through a pipe of uniform bore running full. In an unsteady, uniform flow, the conditions in cross‐sectional area and velocity vary with time from point to point, for example, a wave traveling along a channel.

This is one of the most important classifications in fluid flow and depends primarily upon the arbitrary disturbances, irregularities, or fluctuations in the flow field, based on the internal characteristics of the flow. In this regard, there are two significant parameters such as velocity and viscosity. If the flow occurs at a relatively low velocity and/or with a highly viscous fluid, resulting in a fluid flow in an orderly manner without fluctuations, the flow is referred to as laminar. As the flow velocity increases and/or the viscosity of fluid decreases, the fluctuations take place gradually, referring to a transition state which is dependent on the fluid viscosity, the flow velocity, and geometric details. The Reynolds number Re is introduced to represent the characteristics of the flow conditions relative to the transition state. As the flow conditions deviate more from the transition state, a more chaotic flow field, that is, turbulent flow, occurs. Increasing Reynolds number increases the chaotic nature of the turbulence. Turbulent flow is, therefore, defined as the characteristic representation of the irregularities in the flow field.

The differences between laminar flow and turbulent flow can be distinguished by the Reynolds number, which is expressed as

(1.43)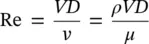

The Reynolds number indicates the ratio of inertial force to viscous force. At high Reynolds numbers the inertia forces dominate, resulting in turbulent flow, while at low Reynolds numbers the viscous forces become dominant, making the flow laminar. In a circular duct, the flow is laminar when Re is less than 2100 and turbulent when Re is greater than 4000. In a duct with a rough surface, the flow is turbulent at Re values as low as 2700.

All actual fluids are normally compressible, leading to a change in their density with pressure. However, in many cases it is assumed during analysis that changes in density are negligibly small. This refers to incompressible flow.

Viscosity is one of the most significant fluid properties, and is defined as a measure of the fluid's resistance to deformation. In gases, the viscosity increases with increasing temperature, resulting in a greater molecular activity and momentum transfer. The viscosity of an ideal gas is a function of molecular dimensions and absolute temperature only, based on the kinetic theory of gases. However, in fluids, molecular cohesion between molecules considerably affects the viscosity, and the viscosity decreases with increasing temperature because of the fact that the cohesive forces are reduced by increasing the temperature of the fluid (causing a decrease in shear stress). This phenomenon results in an increase in the rate of molecular interchange, leading to a net result of a reduction in viscosity. The coefficient of viscosity of an ideal fluid is zero, meaning that an ideal fluid is inviscid, so that no shear stresses occur in the fluid, despite the fact that shear deformations are finite. Nevertheless, all real fluids are viscous.