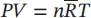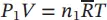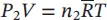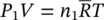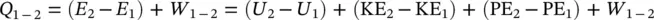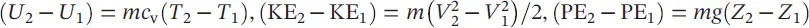Ibrahim Dincer - Thermal Energy Storage Systems and Applications

In thermodynamics, a number of problems involve the mixture of pure substances (e.g. ideal gases). In this regard, it is important to understand related aspects accordingly. Tables 1.2and 1.3summarize the relevant expressions and two ideal‐gas models: the Dalton model and the Amagat model. In the comparison presented, it is assumed that each gas is unaffected by the presence of other gases, and each is treated as an ideal gas. With respect to entropy, it is noted that an increase in entropy is dependent only upon the number of moles of ideal gases, and is independent of the chemical composition. Of course, when the gases in the mixture are distinguished, the entropy increases.

Table 1.3 Comparison of Dalton and Amagat models.

Definition	Dalton model	Amagat model
P , V , T for the mixture	T and V are constant	T and P are constant
P tot= P = P 1+ P 2+ ⋯ + P N	V tot= V = V 1+ V 2+ ⋯ + V N
Ideal‐gas equation for the mixture
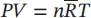Ideal‐gas equations for the components
:	:

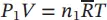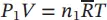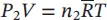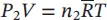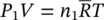Energy can be viewed as the capacity for doing work. Energy can take a number of forms during transfer such as thermal (heat), mechanical (work), electrical, and chemical. Thermal energy flows only from a higher to a lower temperature level unless external energy is added to reverse the process. The rate of energy transfer per unit time is called power .

The definitive experiment that showed that heat was a form of energy convertible into other forms, was carried out by a Scottish physicist, James Joule. Heat is the thermal form of energy, and heat transfer takes place when a temperature difference exists within a medium or between different media. Heat always requires a difference in temperature for its transfer. Higher temperature differences provide higher heat transfer rates. The units for heat are joules or kilojoules in the International system and the foot pound‐force or British thermal unit (Btu) in the English system. Following a common convention in thermodynamic calculations, heat transfer to a system is considered positive , while heat transfer from a system is negative . If there is no heat transfer involved in a process, it is called adiabatic .

Work is the energy that is transferred by a difference in pressure or force of any kind and is subdivided into shaft work and flow work. Shaft work is the mechanical energy used to drive a mechanism such as a pump, compressor, or turbine. Flow work is the energy transferred into a system by fluid flowing into, or out of, the system. Both forms are usually expressed in kilojoules and on a unit mass basis as kJ/kg. By usual convention, work done by a system is considered positive and work done on a system (work input) is considered negative. The unit for power or rate of work is joule per second, which is a Watt (W).

Thermodynamics is the science of energy and entropy, and the basis of thermodynamics is experimental observation. In thermodynamics, such observations were formed into four basic laws: the zeroth, first, second, and third laws of thermodynamics. The first and second laws of thermodynamics are the most common tools in practice due to the fact that transfers and conversions of energy are governed by these two laws, and in this chapter, we focus on these two laws.

The first law of thermodynamics (FLT) can be defined as the law of conservation of energy and states that in a closed system energy can be neither created nor destroyed. For a change of state from an initial state 1 to a final state 2 with a constant amount of matter, the first law can be formulated as follows:

(1.42)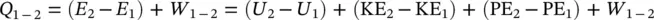

where,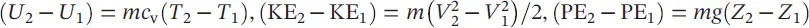

As is clear in Eq. (1.42), we broaden the definition of energy to include kinetic and potential energies in addition to internal energy. An important consequence of the first law is that the internal energy change resulting from a process is independent of the thermodynamic path followed by the system, and of the paths followed by the processes, for example, heat transfer and work. In turn, the rate at which the internal energy content of the system changes is dependent only on the rates at which heat is added and work is done (when kinetic and potential energies are neglected).

As mentioned earlier, the first law is the energy‐conservation principle. The second law of thermodynamics (SLT) is instrumental in determining the inefficiencies of practical thermodynamic systems, and indicates that it is impossible to have 100% efficiency in energy conversion. The classical statements, such as the Kelvin–Plank statement and the Clausius statement, help us formulate the second law:

The Kelvin–Plank statement: It is impossible to construct a device operating in a cycle (e.g. heat engine), that accomplishes only the extraction of heat from some source and its complete conversion to work. This statement describes the impossibility to have a heat engine with a thermal efficiency of 100%.

The Clausius statement: It is impossible to construct a device operating in a cycle (e.g. refrigerator and heat pump), that transfers heat from a low‐temperature (cooler) region to a high‐temperature (hotter) region.

A simple way to illustrate the implications of both the first and second laws is a desktop game that consists of several pendulums (made of metal balls), one in contact with the other. When you raise the first of the balls, you give energy to the system in the form of potential energy. Releasing this ball allows it to gain kinetic energy at the expense of potential energy. When this ball hits the second ball, a small elastic deformation transforms the kinetic energy again into a form of potential energy. The energy is transferred from one ball to the other. The last ball again gains kinetic energy, which allows it to rise. The cycle continues, with the ball rising every time to a slightly lower level, until it finally stops. The first law concerns why the balls keep moving, while the second law explains why they do not do it forever. In this game, the energy is lost in the form of sound and heat, causing the decline in motion.