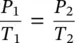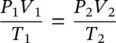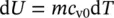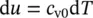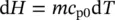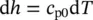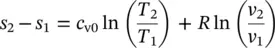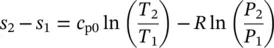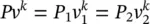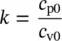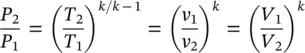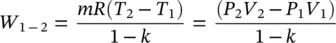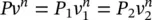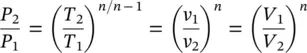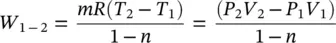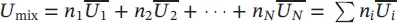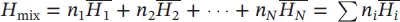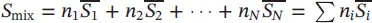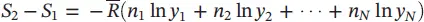Ibrahim Dincer - Thermal Energy Storage Systems and Applications

If temperature increases at constant volume, the pressure of a gas varies directly with its absolute temperature in K as:

(1.27)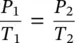

Equations (1.26)and (1.27)are known as Charles' law . If both temperature and pressure change at the same time, the combined ideal‐gas equation can be written as:

(1.28)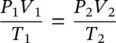

For a given mass, the internal energy of an ideal gas can be written as a function of temperature, since c v0is constant, as shown below:

(1.29)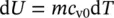

and the specific internal energy becomes

(1.30)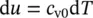

The enthalpy equation for an ideal gas, based on h = u + Pv , can be written as

(1.31)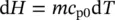

and the specific enthalpy then becomes

(1.32)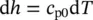

The entropy change of an ideal gas, based on the general entropy equation in terms of T d s = d u + P d v and T d s = d h − v d P as well as on the ideal‐gas equation Pv = RT , can be obtained in two ways by substituting Eqs. (1.29)and (1.30):

(1.33)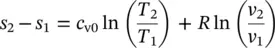

and

(1.34)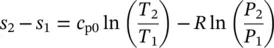

For a reversible adiabatic process, the ideal‐gas equation in terms of the initial and final states under Pv k= constant can be written as:

(1.35)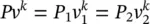

where k denotes the adiabatic exponent (the specific heat ratio ) as a function of temperature:

(1.36)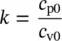

On the basis of Eq. (1.35)and the ideal‐gas equation, the following expression can be obtained:

(1.37)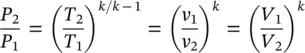

Consider a closed system containing an ideal gas, undergoing an adiabatic reversible process. The gas has constant specific heats. The work can be derived from the first law of thermodynamics (FLT) as follows:

(1.38)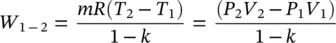

Equation (1.38)can also be derived from the general work relation, W = P d V .

For a reversible polytropic process, the only difference is the polytropic exponent n which shows the deviation in a log P and log V diagram, leading to the slope. Equations can be rewritten with the polytropic exponent under Pv n= constant as

(1.39)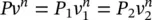

and

(1.40)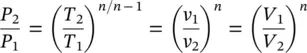

which results in

(1.41)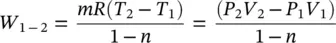

To provide a clear understanding of the polytropic exponent, it is important to show the values of n for four types of polytropic processes for ideal gases ( Figure 1.5):

n = 0 for isobaric process (P = constant)

n = 1 for isothermal process (T = constant)

n = k for isentropic process (s = constant)

n = ∞ for isochoric process (v = constant)

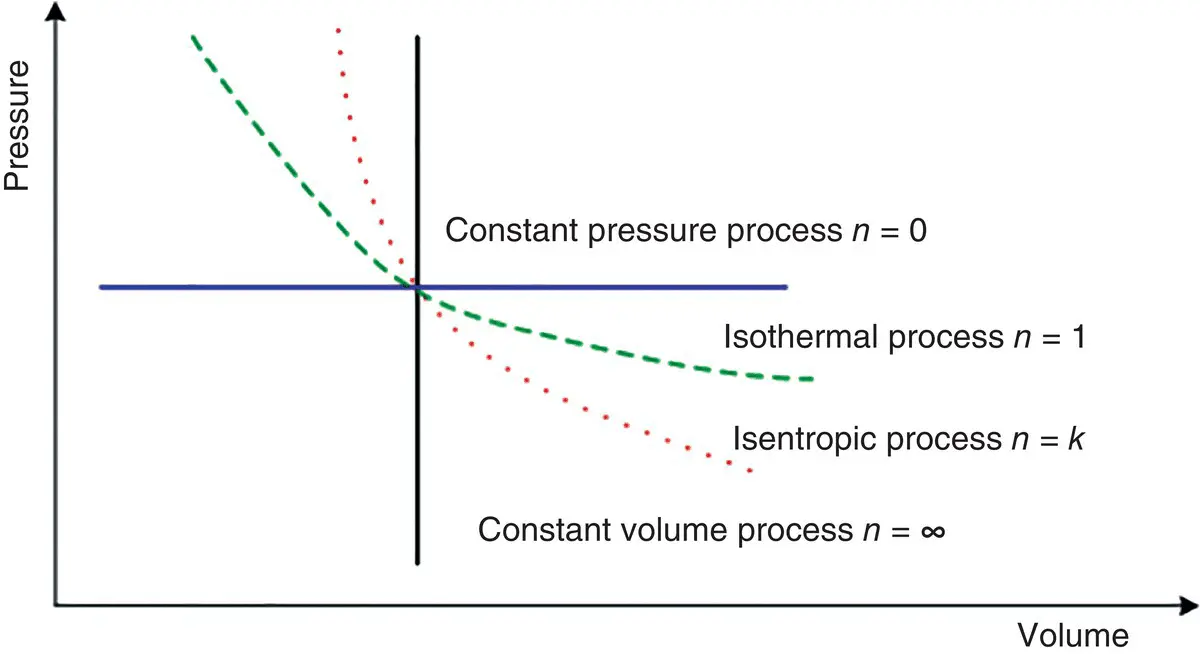
Figure 1.5 Representation of four polytropic processes on a pressure–volume diagram.

Table 1.2 Equations for gas and gas mixtures and relevant models.

Definition	Dalton model and Amagat model
Total mass of a mixture of N components	m tot= m 1+ m 2+ ⋯ + m N= ∑ m i
Total number of moles of a mixture of N components	n tot= n 1+ n 2+ ⋯ + n N= ∑ n i
Mass fraction for each component	c i= m i/ m tot
Mole fraction for each component	y i= n i/ n tot= P i/ P tot= V i/ V tot
Molecular weight of the mixture	M mix= m tot/ n tot= ∑ n i M i/ n tot= ∑ y i M i
Internal energy of the mixture
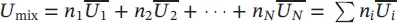Enthalpy of the mixture
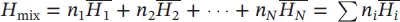Entropy of the mixture
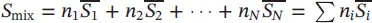Entropy difference for the mixture

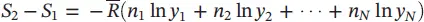As can be seen in Figure 1.5, there are two quadrants where n varies from zero to infinity and where it has a positive value. The slope of any curve is an important consideration when a reciprocating engine or compressor cycle is under consideration.