Similarly I kcan be related to the maximal conductance 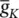 , activation variable a K, and a driving force ( E – E K) as:
, activation variable a K, and a driving force ( E – E K) as:
(3.17) 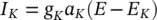
and I leakis related to the maximal conductance 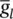 and a driving force ( E – E l) as:
and a driving force ( E – E l) as:
(3.18) 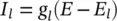
The changes in the variables a Na , a k , and h Navary from 0 to 1 according to the following equations:
(3.19) 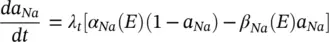
(3.20) 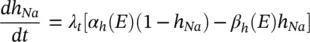
(3.21) 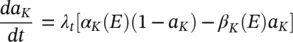
where α ( E ) and β ( E ) are respectively forward and backward rate functions and λ tis a temperature‐dependent factor. The forward and backward parameters depend on voltage and were empirically estimated by Hodgkin and Huxley as:
(3.22) 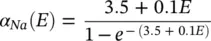
(3.23) 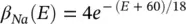
(3.24) 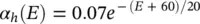
(3.25) 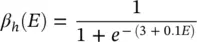
(3.26) 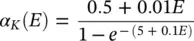
(3.27) 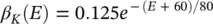
As stated in the Simulator for Neural Networks and Action Potentials (SNNAP) literature [12], the α ( E ) and β ( E ) parameters have been converted from the original Hodgkin–Huxley version to agree with the present physiological practice where depolarization of the membrane is taken to be positive. In addition, the resting potential has been shifted to –60 mV (from the original 0 mV). These equations are used in the model described in the SNNAP. In Figure 3.4an AP has been simulated. For this model the parameters are set to C m= 1.1 μF cm −2, 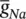 = 100 ms cm −2,
= 100 ms cm −2, 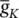 = 35 mS cm −2,
= 35 mS cm −2, 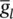 = 0.35 mS cm −2, and E Na = 60 mV.
= 0.35 mS cm −2, and E Na = 60 mV.
The simulation can run to generate a series of APs as practically happens in the case of event‐related potential (ERP) signals. If the maximal ionic conductance of the potassium current 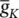 , is reduced the model will show a higher resting potential. Also, for
, is reduced the model will show a higher resting potential. Also, for 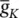 = 16 mS cm −2, the model will begin to exhibit oscillatory behaviour. Figure 3.5shows the result of a Hodgkin–Huxley oscillatory model with reduced maximal potassium conductance.
= 16 mS cm −2, the model will begin to exhibit oscillatory behaviour. Figure 3.5shows the result of a Hodgkin–Huxley oscillatory model with reduced maximal potassium conductance.
The SNNAP can also model bursting neurons and central pattern generators. This stems from the fact that many neurons show cyclic spiky activities followed by a period of inactivity. Several invertebrate as well as mammalian neurons are bursting cells and exhibit alternating periods of high‐frequency spiking behaviour followed by a period of no spiking activity.
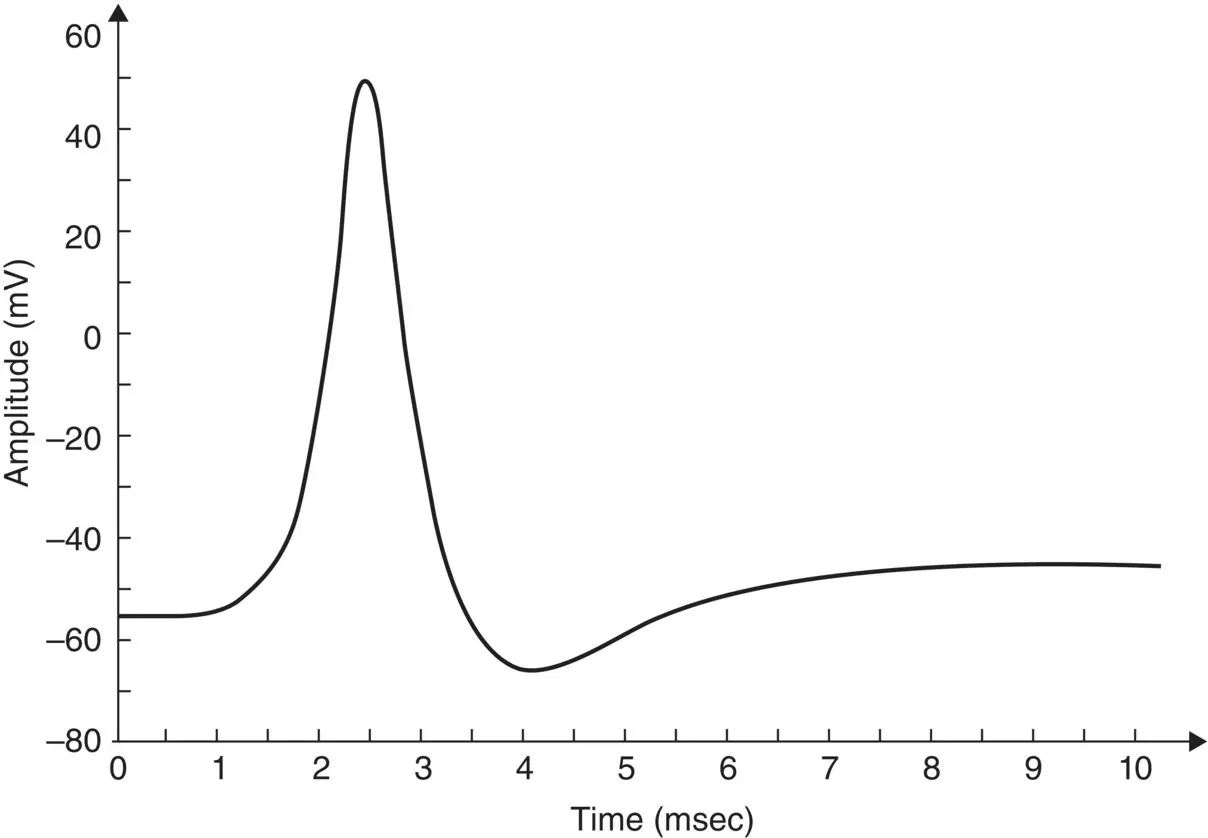
Figure 3.4 A single AP in response to a transient stimulation based on the Hodgkin–Huxley model. The initiated time is at t = 0.4 ms and the injected current is 80 μA cm −2for a duration of 0.1 ms. The selected parameters are C m= 1.2 μF cm −2, 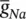 = 100 mS cm −2,
= 100 mS cm −2, 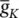 = 35 mS cm −2,
= 35 mS cm −2, 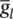 = 0.35 mS cm −2, and E Na = 60 mV.
= 0.35 mS cm −2, and E Na = 60 mV.
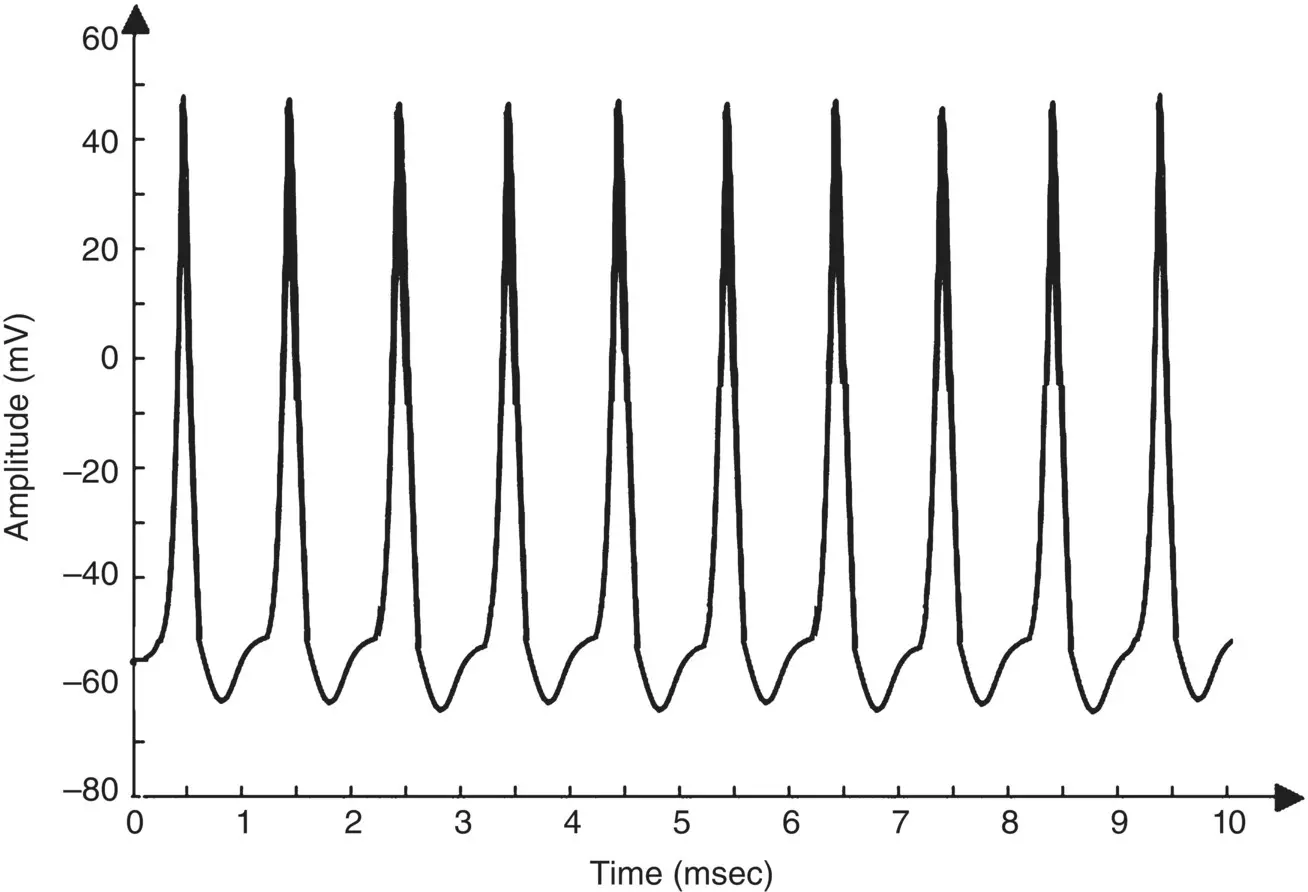
Figure 3.5 The AP from a Hodgkin–Huxley oscillatory model with reduced maximal potassium conductance.
A simpler model than that of Hodgkin–Huxley for simulating spiking neurons is the Morris–Lecar model [14]. This model is a minimal biophysical model, which generally exhibits single AP. This model considers that the oscillation of a slow calcium wave depolarizing the membrane leads to a bursting state. The Morris–Lecar model was initially developed to describe the behaviour of barnacle muscle cells. The governing equations relating the membrane potential ( E ) and potassium activation w kto the activation parameters are given as:
(3.28) 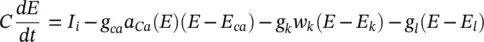
(3.29) 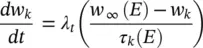
where I iis the combination of three ionic currents, calcium (Ca), potassium (K) and leak ( l ) and similar to the Hodgkin–Huxley model, are products of a maximal conductance 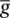 , activation components (in such as a Ca, w k), and the driving force E . The changes in the potassium activation variable w kis proportional to a steady‐state activation function w ∞( E ) (a sigmoid curve) and a time‐constant function τ k( E ) (a bell‐shaped curve). These functions are respectively defined as:
, activation components (in such as a Ca, w k), and the driving force E . The changes in the potassium activation variable w kis proportional to a steady‐state activation function w ∞( E ) (a sigmoid curve) and a time‐constant function τ k( E ) (a bell‐shaped curve). These functions are respectively defined as:
Читать дальше

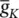 , activation variable a K, and a driving force ( E – E K) as:
, activation variable a K, and a driving force ( E – E K) as: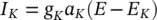
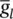 and a driving force ( E – E l) as:
and a driving force ( E – E l) as: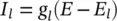
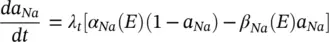
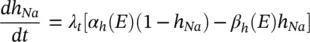
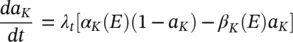
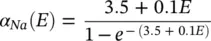
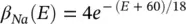
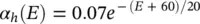
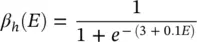
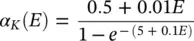
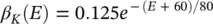
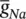 = 100 ms cm −2,
= 100 ms cm −2, 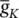 = 35 mS cm −2,
= 35 mS cm −2, 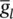 = 0.35 mS cm −2, and E Na = 60 mV.
= 0.35 mS cm −2, and E Na = 60 mV.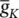 , is reduced the model will show a higher resting potential. Also, for
, is reduced the model will show a higher resting potential. Also, for 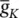 = 16 mS cm −2, the model will begin to exhibit oscillatory behaviour. Figure 3.5shows the result of a Hodgkin–Huxley oscillatory model with reduced maximal potassium conductance.
= 16 mS cm −2, the model will begin to exhibit oscillatory behaviour. Figure 3.5shows the result of a Hodgkin–Huxley oscillatory model with reduced maximal potassium conductance.
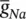 = 100 mS cm −2,
= 100 mS cm −2, 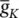 = 35 mS cm −2,
= 35 mS cm −2, 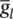 = 0.35 mS cm −2, and E Na = 60 mV.
= 0.35 mS cm −2, and E Na = 60 mV.
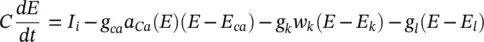
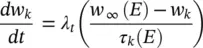
 , activation components (in such as a Ca, w k), and the driving force E . The changes in the potassium activation variable w kis proportional to a steady‐state activation function w ∞( E ) (a sigmoid curve) and a time‐constant function τ k( E ) (a bell‐shaped curve). These functions are respectively defined as:
, activation components (in such as a Ca, w k), and the driving force E . The changes in the potassium activation variable w kis proportional to a steady‐state activation function w ∞( E ) (a sigmoid curve) and a time‐constant function τ k( E ) (a bell‐shaped curve). These functions are respectively defined as:










