Saeid Sanei - EEG Signal Processing and Machine Learning

64 64 Jacobson, S. and Jerrier, H. (2000). EEG in delirium. Seminars in Clinical Neuropsychiatry 5 (2): 86–92.

65 65 Onoe, S. and Nishigaki, T. (2004). EEG spectral analysis in children with febrile delirium. Brain & Development 26 (8): 513–518.

66 66 Brunovsky, M., Matousek, M., Edman, A. et al. (2003). Objective assessment of the degree of dementia by means of EEG. Neuropsychobiology 48 (1): 19–26.

67 67 Koenig, T., Prichep, L., Dierks, T. et al. (2005). Decreased EEG synchronization in Alzheimer's disease and mild cognitive impairment. Neurobiology of Aging 26 (2): 165–171.

68 68 Babiloni, C., Binetti, G., Cassetta, E. et al. (2006). Sources of cortical rhythms change as a function of cognitive impairment in pathological aging: a multicenter study. Clinical Neurophysiology 117 (2): 252–268.

69 69 Bauer, G. and Bauer, R. (1999). EEG, drug effects, and central nervous system poisoning, Chapter 35. In: Electroencephalography, Basic Principles, Clinical Applications, and Related Fields, 4e (eds. E. Niedermeyer and F.L. Da Silva), 671–691. Lippincott Williams & Wilkins.

70 70 Beck, E. and Daniel, P.M. (1969). Degenerative diseases of the central nervous system transmissible to experimental animals. Postgraduate Medical Journal 45 (524): 361–370.

71 71 Naidu, S. and Niedermeyer, E. (1999). Digenerative disorders of the central nervous system, Chapter 20. In: Electroencephalography, Basic Principles, Clinical Applications, and Related Fields, 4e (eds. E. Niedermeyer and F.L. Da Silva), 360–382. Lippincott Williams & Wilkins.

Generation of electrical potentials or magnetic fields, measurable from the brain, is due to a nonlinear sum/distribution of electrochemical active potentials within all the neurons involved in cognitive or movement‐related processes. An accurate model that can link the chemical processes within corresponding neurons generating the active potentials is hard to achieve due to the involvement of various chemicals and chemical processes. Some models, however, have been introduced since 1950s.

Neurons may be considered as signal converters. The brain is a complicated network of a tremendous number of neurons. Figure 3.1a shows a small network of three neurons. Each axon is extended from a soma which is the main neuron body. Neurons transmit and exchange electric signals called action potentials (APs) or spikes, among each other. Neurons receive the spikes at a synapse. Then, the electric signals or information is transmitted in the direction from a dendrite to an axon. Figure 3.1b illustrates the waveform of APs which have an amplitude of approximately 100 mV in the human brain.

Typical neurons do not generate any spikes without input signals which often come from other neurons. A sufficiently large input pulse causes a neuron to generate an output spike whereas no output spike is generated by a small input. Therefore, a neuron possesses a threshold or all‐or‐none characteristic. There is a special period or timing called the refractory period (the timing of the downstroke of the AP) in which the neuron cannot produce any output spike even though a sufficient amount of inputs is applied to the neuron. Hence, a neuron may be considered as a device which transforms or converts the input spike train to another spike train where each output spike (AP), as we will see later, is the integral of a number of input spikes.

The popular physiological models aim to best simulate the coupling between two or more neurons. In [1] three models for generation of brain potentials have been introduced and compared.

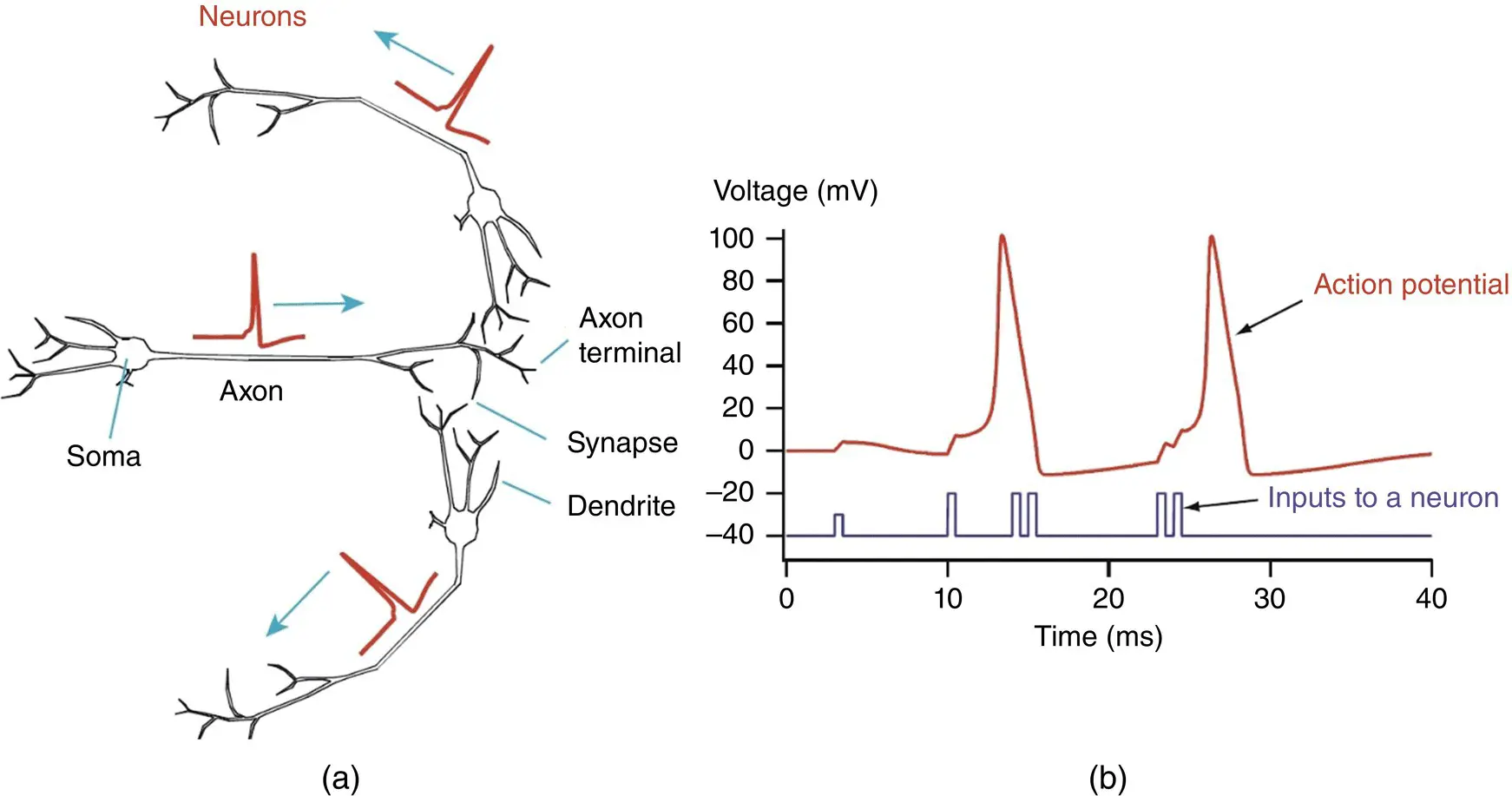
Figure 3.1 (a) A network of three neurons that exchange electric signals, namely action potentials. (b) The waveform of action potentials including the input to a neuron.

For coupling two neurons two integrate‐and‐fire neurons with mutual excitatory or inhibitory coupling have been described in [1]. The neurons with activation variables x ifor i = 1, 2, satisfy:

(3.1)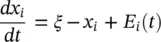

where ξ >1 is a constant, 0 < x i< 1, and E i( t ) is the synaptic input to neuron i . Neuron i fires when x i= 1 and hen resets x ito 0. If cell j ≠ i fires at time t jthe function E iis augmented to E i( t ) + E s( t‐t j), where E sis the contribution coming from one spike [1]. In an example in [1] this function is selected as:

(3.2)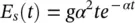

where g and α are parameters determining the strength and speed of the synapse respectively and the factor of α 2in (3.2)normalizes the integral of E sover time to the value g . In the considered cases the two neurons continue firing periodically when they are coupled together. Assuming that neuron 1 fires at times t = nT, where T is the period and n is an integer, while neuron 2 fires at t = ( n − φ ) T . Therefore, both neurons are firing at the same frequency but are separated by a phase φ . We wish to determine possible values of the phase difference φ and conditions under which they arise.

Neuronal synchronization processes, measured with brain imaging data, can be described using weakly coupled oscillator (WCO) models. Dynamic causal modelling (DCM) is used to fit the WCOs to brain imaging data and so make inferences about the structure of neuronal interactions [2]. The complex behaviours are mediated by the interaction of particular brain regions. Recent studies agreed that such interactions may be instantiated by the transient synchronization of oscillatory neuronal ensembles [3]. For example, contour detection is accompanied by gamma band synchronization in distant parts of visual cortex, multimodal object processing by parieto‐temporal synchronization in the beta band [4] and spatial memory processes by hippocampal–prefrontal synchronization in the theta band [2, 5]. DCM allows for different model structures to be compared using Bayesian model selection [6]. In [2] DCM has been extended to the study of phase coupling. One direction is based on the WCO models in which the rate of change of phase of one oscillator is related to the phase differences between itself and other oscillators [7].

The WCO theory applies to system dynamics close to limit cycles. By assuming that weak coupling leads to only small perturbations away from these cycles, one can reduce a high‐dimensional system of differential equations to one based solely on the phases of the oscillators, and pairwise interactions between them [2].

Dynamics on the limit cycle are given by [2]:

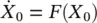
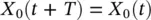
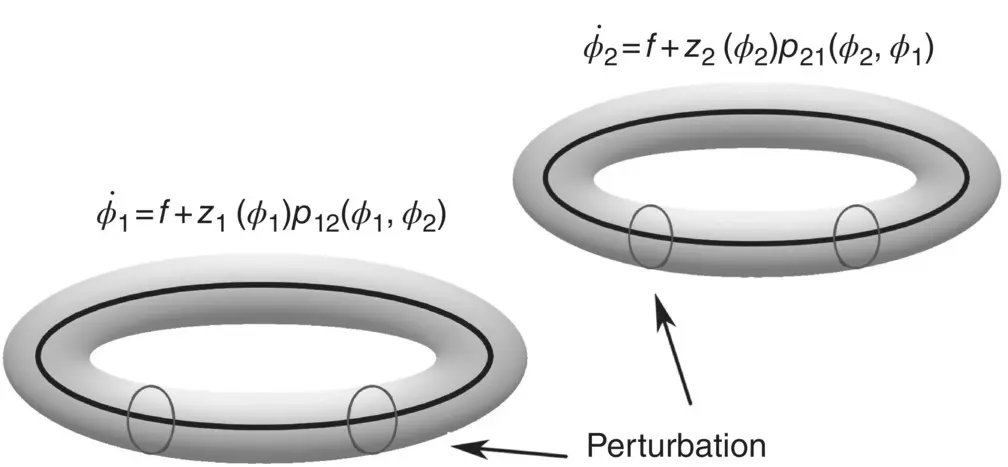
Figure 3.2 A pair of oscillators weakly coupled via the perturbation function p ( φ 1, φ 2).