Iain Pardoe - Applied Regression Modeling
Здесь есть возможность читать онлайн «Iain Pardoe - Applied Regression Modeling» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Applied Regression Modeling
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Applied Regression Modeling: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Applied Regression Modeling»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
delivers a concise but comprehensive treatment of the application of statistical regression analysis for those with little or no background in calculus. Accomplished instructor and author Dr. Iain Pardoe has reworked many of the more challenging topics, included learning outcomes and additional end-of-chapter exercises, and added coverage of several brand-new topics including multiple linear regression using matrices.
The methods described in the text are clearly illustrated with multi-format datasets available on the book's supplementary website. In addition to a fulsome explanation of foundational regression techniques, the book introduces modeling extensions that illustrate advanced regression strategies, including model building, logistic regression, Poisson regression, discrete choice models, multilevel models, Bayesian modeling, and time series forecasting. Illustrations, graphs, and computer software output appear throughout the book to assist readers in understanding and retaining the more complex content.
covers a wide variety of topics, like:
Simple linear regression models, including the least squares criterion, how to evaluate model fit, and estimation/prediction Multiple linear regression, including testing regression parameters, checking model assumptions graphically, and testing model assumptions numerically Regression model building, including predictor and response variable transformations, qualitative predictors, and regression pitfalls Three fully described case studies, including one each on home prices, vehicle fuel efficiency, and pharmaceutical patches Perfect for students of any undergraduate statistics course in which regression analysis is a main focus,
also belongs on the bookshelves of non-statistics graduate students, including MBAs, and for students of vocational, professional, and applied courses like data science and machine learning.

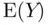 , as
, as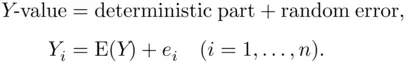
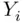 ‐value (the index
‐value (the index 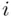 keeps track of the sample observations) can be decomposed into two pieces, a deterministic part that is the same for all values, and a random error part that varies from observation to observation. A convenient choice for the deterministic part is the population mean,
keeps track of the sample observations) can be decomposed into two pieces, a deterministic part that is the same for all values, and a random error part that varies from observation to observation. A convenient choice for the deterministic part is the population mean, 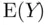 , since then the random errors have a (population) mean of zero. Since
, since then the random errors have a (population) mean of zero. Since 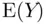 is the same for all
is the same for all 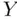 ‐values, the random errors,
‐values, the random errors, 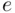 , have the same standard deviation as the
, have the same standard deviation as the 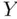 ‐values themselves, that is,
‐values themselves, that is, 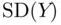 . We can use this decomposition to derive the confidence interval and hypothesis test results of Sections 1.5and 1.6(although it would take more mathematics than we really need for our purposes in this book). Moreover, we can also use this decomposition to motivate the precise form of the uncertainty needed for prediction intervals (without having to get into too much mathematical detail).
. We can use this decomposition to derive the confidence interval and hypothesis test results of Sections 1.5and 1.6(although it would take more mathematics than we really need for our purposes in this book). Moreover, we can also use this decomposition to motivate the precise form of the uncertainty needed for prediction intervals (without having to get into too much mathematical detail). ‐value to be predicted as
‐value to be predicted as 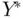 , and decompose this into two pieces as above:
, and decompose this into two pieces as above: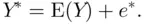
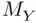 , which represents potential values of repeated sample means, from both sides of this equation:
, which represents potential values of repeated sample means, from both sides of this equation: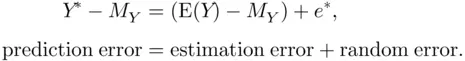
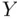 ‐value, we have to worry about both estimation error and random error.
‐value, we have to worry about both estimation error and random error.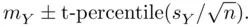
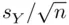 in this formula is an estimate of the standard deviation of the sampling distribution of sample means,
in this formula is an estimate of the standard deviation of the sampling distribution of sample means, 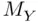 , and is called the standard error of estimation . The square of this quantity,
, and is called the standard error of estimation . The square of this quantity, 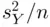 , is the estimated variance of the sampling distribution of sample means,
, is the estimated variance of the sampling distribution of sample means, 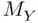 . Then, thinking of
. Then, thinking of 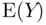 as some fixed, unknown constant,
as some fixed, unknown constant,  is also the estimated variance of the estimation error,
is also the estimated variance of the estimation error, 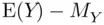 , in expression ( 1.1).
, in expression ( 1.1).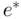 , in expression ( 1.1) is
, in expression ( 1.1) is 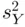 . It can then be shown that the estimated variance of the prediction error,
. It can then be shown that the estimated variance of the prediction error, 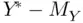 , in expression ( 1.1) is
, in expression ( 1.1) is 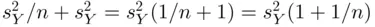 . Then,
. Then, 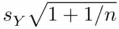 is called the standard error of prediction .
is called the standard error of prediction .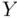 ‐value, as
‐value, as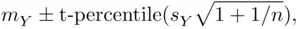
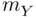 is the sample mean,
is the sample mean, 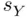 is the sample standard deviation,
is the sample standard deviation, 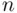 is the sample size, and the t‐percentile comes from a t‐distribution with
is the sample size, and the t‐percentile comes from a t‐distribution with 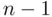 degrees of freedom.
degrees of freedom.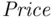 picked at random from the population of single‐family home sale prices is calculated as
picked at random from the population of single‐family home sale prices is calculated as










