Iain Pardoe - Applied Regression Modeling
Здесь есть возможность читать онлайн «Iain Pardoe - Applied Regression Modeling» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Applied Regression Modeling
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Applied Regression Modeling: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Applied Regression Modeling»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
delivers a concise but comprehensive treatment of the application of statistical regression analysis for those with little or no background in calculus. Accomplished instructor and author Dr. Iain Pardoe has reworked many of the more challenging topics, included learning outcomes and additional end-of-chapter exercises, and added coverage of several brand-new topics including multiple linear regression using matrices.
The methods described in the text are clearly illustrated with multi-format datasets available on the book's supplementary website. In addition to a fulsome explanation of foundational regression techniques, the book introduces modeling extensions that illustrate advanced regression strategies, including model building, logistic regression, Poisson regression, discrete choice models, multilevel models, Bayesian modeling, and time series forecasting. Illustrations, graphs, and computer software output appear throughout the book to assist readers in understanding and retaining the more complex content.
covers a wide variety of topics, like:
Simple linear regression models, including the least squares criterion, how to evaluate model fit, and estimation/prediction Multiple linear regression, including testing regression parameters, checking model assumptions graphically, and testing model assumptions numerically Regression model building, including predictor and response variable transformations, qualitative predictors, and regression pitfalls Three fully described case studies, including one each on home prices, vehicle fuel efficiency, and pharmaceutical patches Perfect for students of any undergraduate statistics course in which regression analysis is a main focus,
also belongs on the bookshelves of non-statistics graduate students, including MBAs, and for students of vocational, professional, and applied courses like data science and machine learning.

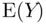 , as
, as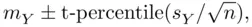
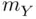 is the sample mean,
is the sample mean, 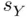 is the sample standard deviation,
is the sample standard deviation, 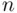 is the sample size, and the t‐percentile comes from a t‐distribution with
is the sample size, and the t‐percentile comes from a t‐distribution with 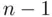 degrees of freedom. In this expression,
degrees of freedom. In this expression, 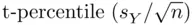 is the margin of error.
is the margin of error.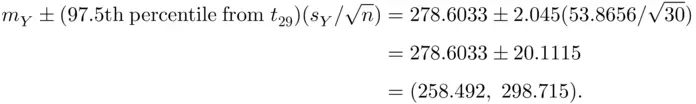
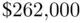 ,
, 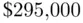 ).
).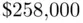 and
and 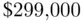 .” This will get you by among friends (as long as none of your friends happen to be expert statisticians). But to provide a more precise interpretation we have to revisit the notion of hypothetical repeated samples. If we were to take a large number of random samples of size 30 from our population of sale prices and calculate a 95% confidence interval for each, then 95% of those confidence intervals would contain the (unknown) population mean. We do not know (nor will we ever know) whether the 95% confidence interval for our particular sample contains the population mean—thus, strictly speaking, we cannot say “the probability that the population mean is in our interval is 0.95.” All we know is that the procedure that we have used to calculate the 95% confidence interval tends to produce intervals that under repeated sampling contain the population mean 95% of the time. Stick with the phrase “95% confident” and avoid using the word “probability” and chances are that no one (not even expert statisticians) will be too offended.
.” This will get you by among friends (as long as none of your friends happen to be expert statisticians). But to provide a more precise interpretation we have to revisit the notion of hypothetical repeated samples. If we were to take a large number of random samples of size 30 from our population of sale prices and calculate a 95% confidence interval for each, then 95% of those confidence intervals would contain the (unknown) population mean. We do not know (nor will we ever know) whether the 95% confidence interval for our particular sample contains the population mean—thus, strictly speaking, we cannot say “the probability that the population mean is in our interval is 0.95.” All we know is that the procedure that we have used to calculate the 95% confidence interval tends to produce intervals that under repeated sampling contain the population mean 95% of the time. Stick with the phrase “95% confident” and avoid using the word “probability” and chances are that no one (not even expert statisticians) will be too offended.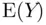 , to be (
, to be ( 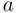 ,
, 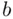 ). Then we can say that we are 95% confident that
). Then we can say that we are 95% confident that 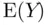 is between
is between 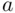 and
and 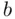 .
.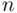 in the degrees of freedom formula comes in), but we lose a degree of freedom for each population parameter that we have to estimate. So, in this chapter, when we are estimating the population mean, the degrees of freedom formula is
in the degrees of freedom formula comes in), but we lose a degree of freedom for each population parameter that we have to estimate. So, in this chapter, when we are estimating the population mean, the degrees of freedom formula is 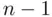 . In Chapter 2, when we will be estimating two population parameters (the intercept and the slope of a regression line), the degrees of freedom formula will be
. In Chapter 2, when we will be estimating two population parameters (the intercept and the slope of a regression line), the degrees of freedom formula will be 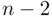 . For the remainder of the book, the general formula for the degrees of freedom in a multiple linear regression model will be
. For the remainder of the book, the general formula for the degrees of freedom in a multiple linear regression model will be 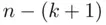 or
or 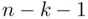 , where
, where 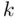 is the number of predictor variables in the model. Note that this general formula actually also works for Chapter 2(where
is the number of predictor variables in the model. Note that this general formula actually also works for Chapter 2(where 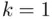 ) and even this chapter (where
) and even this chapter (where 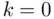 , since a linear regression model with zero predictors is equivalent to estimating the population mean for a univariate dataset).
, since a linear regression model with zero predictors is equivalent to estimating the population mean for a univariate dataset).










