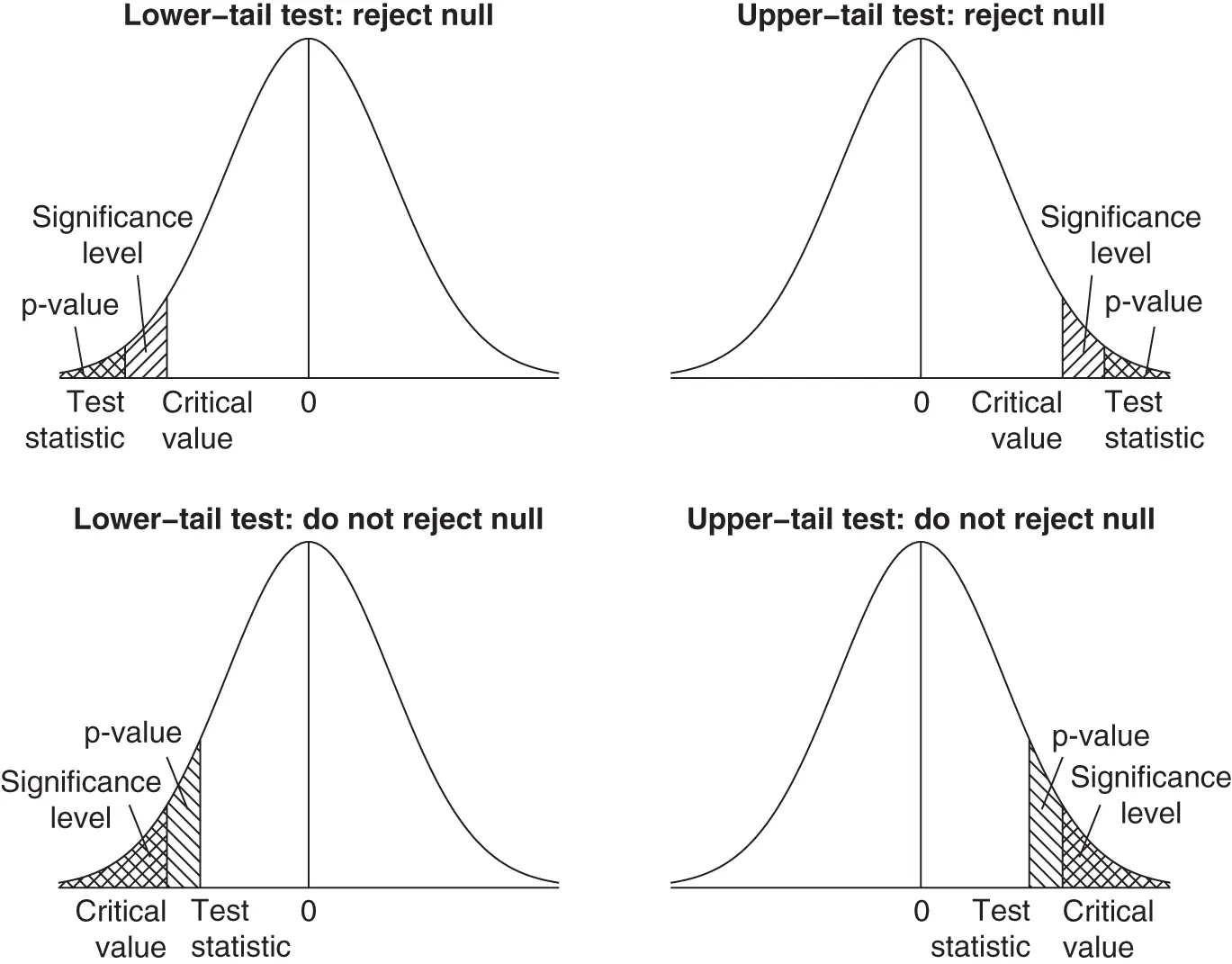
Figure 1.7Relationships between critical values, significance levels, test statistics, and p‐values for one‐tail hypothesis tests.

Figure 1.8Relationships between critical values, significance levels, test statistics, and p‐values for two‐tail hypothesis tests.
Two‐tail tests work similarly, but we have to be careful to work with both tails of the t‐distribution; Figure 1.8illustrates. For the home prices example, we might want to do a two‐tail hypothesis test if we had no prior expectation about how large or small sale prices are, but just wanted to see whether or not the realtor's claim of 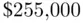 was plausible. The steps involved are as follows (see computer help #24):
was plausible. The steps involved are as follows (see computer help #24):
State null hypothesis: : .
State alternative hypothesis: : .
Calculate test statistic: .
Set significance level: 5%.
Look up t‐table:– critical value: The 97.5th percentile of the t‐distribution with 29 degrees of freedom is 2.045 (from Table C.1); the rejection region is therefore any t‐statistic greater than 2.045 or less than (we need the 97.5th percentile in this case because this is a two‐tail test, so we need half the significance level in each tail).– p‐value: The area to the right of the t‐statistic (2.40) for the t‐distribution with 29 degrees of freedom is less than 0.025 but greater than 0.01 (since from Table C.1 the 97.5th percentile of this t‐distribution is 2.045 and the 99th percentile is 2.462); thus, the upper‐tail area is between 0.01 and 0.025 and the two‐tail p‐value is twice as big as this, that is, between 0.02 and 0.05.
Make decision:– Since the t‐statistic of 2.40 falls in the rejection region, we reject the null hypothesis in favor of the alternative.– Since the p‐value is between 0.02 and 0.05, it must be less than the significance level (0.05), so we reject the null hypothesis in favor of the alternative.
Interpret in the context of the situation: The 30 sample sale prices suggest that a population mean of seems implausible—the sample data favor a value different from this (at a significance level of 5%).
1.6.3 Hypothesis test errors
When we introduced significance levels in Section 1.6.1, we saw that the person conducting the hypothesis test gets to choose this value. We now explore this notion a little more fully.
Whenever we conduct a hypothesis test, either we reject the null hypothesis in favor of the alternative or we do not reject the null hypothesis. “Not rejecting” a null hypothesis is not quite the same as “accepting” it. All we can say in such a situation is that we do not have enough evidence to reject the null—recall the legal analogy where defendants are not found “innocent” but rather are found “not guilty.” Anyway, regardless of the precise terminology we use, we hope to reject the null when it really is false and to “fail to reject it” when it really is true. Anything else will result in a hypothesis test error . There are two types of error that can occur, as illustrated in the following table: Hypothesis test errors
|
|
Decision |
|
|
Do not reject 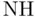 |
Reject 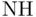 in favor of in favor of 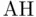 |
| Reality |
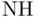 true true |
Correct decision |
Type 1 error |
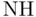 false false |
Type 2 error |
Correct decision |
A type 1 error can occur if we reject the null hypothesis when it is really true—the probability of this happening is precisely the significance level. If we set the significance level lower, then we lessen the chance of a type 1 error occurring. Unfortunately, lowering the significance level increases the chance of a type 2 error occurring—when we fail to reject the null hypothesis but we should have rejected it because it was false. Thus, we need to make a trade‐off and set the significance level low enough that type 1 errors have a low chance of happening, but not so low that we greatly increase the chance of a type 2 error happening. The default value of 5% tends to work reasonably well in many applications at balancing both goals. However, other factors also affect the chance of a type 2 error happening for a specific significance level. For example, the chance of a type 2 error tends to decrease the greater the sample size.
1.7 Random Errors and Prediction
So far, we have focused on estimating a univariate population mean, 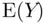 , and quantifying our uncertainty about the estimate via confidence intervals or hypothesis tests. In this section, we consider a different problem, that of “prediction.” In particular, rather than estimating the mean of a population of
, and quantifying our uncertainty about the estimate via confidence intervals or hypothesis tests. In this section, we consider a different problem, that of “prediction.” In particular, rather than estimating the mean of a population of 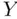 ‐values based on a sample,
‐values based on a sample,  , consider predicting an individual
, consider predicting an individual 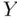 ‐value picked at random from the population.
‐value picked at random from the population.
Intuitively, this sounds like a more difficult problem. Imagine that rather than just estimating the mean sale price of single‐family homes in the housing market based on our sample of 30 homes, we have to predict the sale price of an individual single‐family home that has just come onto the market. Presumably, we will be less certain about our prediction than we were about our estimate of the population mean (since it seems likely that we could be further from the truth with our prediction than when we estimated the mean—for example, there is a chance that the new home could be a real bargain or totally overpriced). Statistically speaking, Figure 1.5illustrates this “extra uncertainty” that arises with prediction—the population distribution of data values,  (more relevant to prediction problems), is much more variable than the sampling distribution of sample means,
(more relevant to prediction problems), is much more variable than the sampling distribution of sample means, 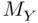 (more relevant to mean estimation problems).
(more relevant to mean estimation problems).
We can tackle prediction problems with a similar process to that of using a confidence interval to tackle estimating a population mean. In particular, we can calculate a prediction interval of the form “point estimate  uncertainty” or “(point estimate
uncertainty” or “(point estimate  uncertainty, point estimate
uncertainty, point estimate  uncertainty).” The point estimate is the same one that we used for estimating the population mean, that is, the observed sample mean,
uncertainty).” The point estimate is the same one that we used for estimating the population mean, that is, the observed sample mean, 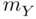 . This is because
. This is because 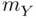 is an unbiased estimate of the population mean,
is an unbiased estimate of the population mean, 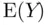 , and we assume that the individual
, and we assume that the individual 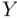 ‐value we are predicting is a member of this population. As discussed in the preceding paragraph, however, the “uncertainty” is larger for prediction intervals than for confidence intervals. To see how much larger, we need to return to the notion of a model that we introduced in Section 1.2.
‐value we are predicting is a member of this population. As discussed in the preceding paragraph, however, the “uncertainty” is larger for prediction intervals than for confidence intervals. To see how much larger, we need to return to the notion of a model that we introduced in Section 1.2.
Читать дальше



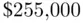 was plausible. The steps involved are as follows (see computer help #24):
was plausible. The steps involved are as follows (see computer help #24):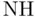
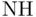 in favor of
in favor of 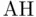
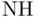 true
true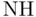 false
false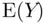 , and quantifying our uncertainty about the estimate via confidence intervals or hypothesis tests. In this section, we consider a different problem, that of “prediction.” In particular, rather than estimating the mean of a population of
, and quantifying our uncertainty about the estimate via confidence intervals or hypothesis tests. In this section, we consider a different problem, that of “prediction.” In particular, rather than estimating the mean of a population of 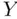 ‐values based on a sample,
‐values based on a sample,  , consider predicting an individual
, consider predicting an individual 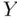 ‐value picked at random from the population.
‐value picked at random from the population. (more relevant to prediction problems), is much more variable than the sampling distribution of sample means,
(more relevant to prediction problems), is much more variable than the sampling distribution of sample means, 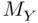 (more relevant to mean estimation problems).
(more relevant to mean estimation problems). uncertainty” or “(point estimate
uncertainty” or “(point estimate  uncertainty, point estimate
uncertainty, point estimate  uncertainty).” The point estimate is the same one that we used for estimating the population mean, that is, the observed sample mean,
uncertainty).” The point estimate is the same one that we used for estimating the population mean, that is, the observed sample mean, 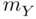 . This is because
. This is because 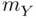 is an unbiased estimate of the population mean,
is an unbiased estimate of the population mean, 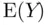 , and we assume that the individual
, and we assume that the individual  ‐value we are predicting is a member of this population. As discussed in the preceding paragraph, however, the “uncertainty” is larger for prediction intervals than for confidence intervals. To see how much larger, we need to return to the notion of a model that we introduced in Section 1.2.
‐value we are predicting is a member of this population. As discussed in the preceding paragraph, however, the “uncertainty” is larger for prediction intervals than for confidence intervals. To see how much larger, we need to return to the notion of a model that we introduced in Section 1.2.










