Aiden A. Bruen - Cryptography, Information Theory, and Error-Correction

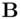receives 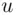and calculates .

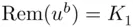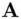receives 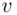and calculates .

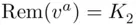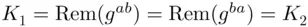Now, and 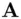, 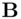are in possession of a common secret key 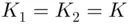, since .

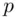
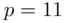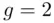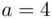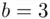, , , . Then: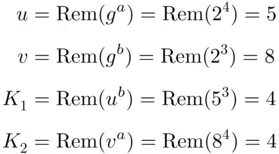

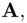
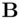The common secret key possessed by is 4. In calculating, we may use the shortcuts that were introduced earlier in Chapter 3.

The security of the Diffie–Hellman (DH) key‐exchange rests on the assumption that the DH problem described now cannot be solved in a reasonable amount of time, i.e. is intractable.

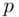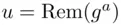Given a prime , , and 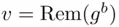, find .

A (potentially) more general problem is the discrete log problem.

(We remark that in the DH problem it suffices to consider the cases when and .)

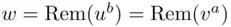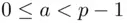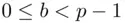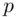Given a prime and 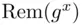, where 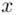is one of the numbers , find .

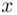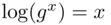It is called the discrete log problem because when 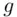is chosen as the logarithmic base. A solution to the discrete log problem (i.e. finding an algorithm for calculating 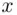in a reasonable amount of time) would imply a solution to the Diffie–Hellman problem. The converse statement is not known to be true, although there is experimental evidence pointing in that direction.

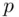We should point out that, for security, one wants to be well‐behaved meaning that has large factors. The ideal case is when 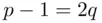, where 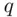itself is prime. For example, take 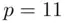so 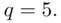In the ideal case, 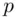has the greatest possible number of different generators (for its size) so that it is easy to find a generator. However, such primes 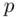, known as Sophie‐Germainprimes, are conjectured to be rare. In any event, only a finite number are known to exist.