3.5 Attacks, Security, Catch‐22 of Cryptography
There are many attacks on cryptosystems, i.e. attempts by an intruder to break the system by recovering the key and the message or the message directly. By far, the attack most difficult to defend against is an impersonation or man‐in‐the‐middle attack . Another type of attack is a brute‐force attack(see Section 7.3) in which the attacker systematically tries all possible keys on the key‐space. A variety of attacks are discussed in Chapter 7.
A basic issue in cryptography is this: If we are trying to guess one of 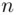 possible passwords in order to log on (or
possible passwords in order to log on (or 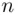 possible keys say), then how many guesses will we have to make on average until we are successful? The answer is easy to find .
possible keys say), then how many guesses will we have to make on average until we are successful? The answer is easy to find .
On the average, when trying to guess one of 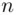 possible keys, we only need
possible keys, we only need 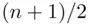 guesses.
guesses.
First, we explain the concept of average value which is discussed also in Chapter 9. Suppose that, in a class of 6 students, 3 get 70%, 2 get 80%, and 1 gets 92%. What is the average grade? One can write this average as 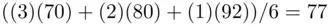 . So the average grade is 77%. We could also calculate the average as
. So the average grade is 77%. We could also calculate the average as 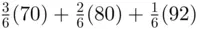 , where
, where 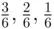 are the probabilities of getting 70, 80, and 92, respectively. Now, we proceed to the proof.
are the probabilities of getting 70, 80, and 92, respectively. Now, we proceed to the proof.
Proof.The probability of guessing correctly the first time is 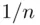 . To get it right in exactly 2 guesses, we must get it wrong on the first guess and then, having discarded the unsuccessful guess, we must guess correctly on the next attempt. So the probability of being successful in exactly 2 guesses is
. To get it right in exactly 2 guesses, we must get it wrong on the first guess and then, having discarded the unsuccessful guess, we must guess correctly on the next attempt. So the probability of being successful in exactly 2 guesses is 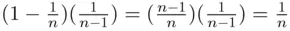 . Similarly, the probability of being successful in exactly
. Similarly, the probability of being successful in exactly 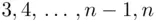 guesses is also
guesses is also 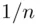 . To get the average number of guesses, we multiply the number of guesses by the probability and add up. This gives the average number of trials until success to be
. To get the average number of guesses, we multiply the number of guesses by the probability and add up. This gives the average number of trials until success to be 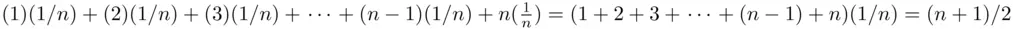 . So on average, you get the correct password after
. So on average, you get the correct password after 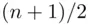 attempts.
attempts.
Public key algorithms and symmetric algorithms were compared in Section 3.4. With any public key algorithm such as RSA (or elliptic curve cryptography), given sufficient time and computing power, the eavesdropper is certain to recover the message . In fact, with RSA it is generally quicker to try to solve the factoring problem than to try all possible values of 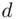 (brute‐force). One of the main advantages of RSA is the convenience and low cost, especially for e‐commerce. Advantages of symmetric systems include improved security and the speed.
(brute‐force). One of the main advantages of RSA is the convenience and low cost, especially for e‐commerce. Advantages of symmetric systems include improved security and the speed.
A difficulty with key systems is the key distribution problem , i.e. the problem of getting the common secret key to Aand B. This is eloquently expressed by Professor Lomonaco when he writes about the Catch‐22 of cryptography [Lom98].
Catch‐22 of Cryptography:
To communicate in secret, we must first communicate in secret .
For symmetric encryption, the private key has to be given secretly to each entity, whereas the public keys for each entity are  public!
public!
We have spoken already of the assumption that the encryption algorithms for public key cryptography are assumed to be mathematical one‐way functions. This means that enciphering has the property that its values are easily computed by a computer (i.e. are computed in polynomial time), yet the deciphering algorithm cannot be computed in a reasonable amount of time (even on a computer). In other words, the problem of deciphering the cipher text is intractable.
Of course, we emphasize again that the existence of such mathematical one‐way functions is still in doubt since nobody has discovered a mathematical function that is provably one‐way.
But one‐way functions abound in the physical world, many of them related to time. For example, as Beutelspacher [Beu94] points out, most people are not getting any younger, i.e. the aging function is one‐way!
Another analogy is the telephone directory of any big city. Here each name gets enciphered to the corresponding telephone number. The deciphering algorithm starts with a number and tries to find the corresponding name, a much more daunting task.
One can also make physical analogies concerning the two kinds of cryptography.
For public key cryptography, consider the following scenario: Awants to send a secret message to B. A number of mailboxes are available. Aknows that the mailbox for Bis number 3 (3 is the public key for B). All Ahas to do is to drop the message into mailbox number 3 for B. Then B(but nobody else) can recover the message since Bhas the key to mailbox number 3.
Another system for public key algorithms is as follows: Awants to send a secret message to B. He goes to the hardware store and buys a box and a combination lock marked B(this corresponds to the public key of B). Then Aputs the message in the box, locks the box with the combination lock and mails it to B. When the box arrives, Bopens it, and gets the message because he knows the combination for the lock. Nobody else can open the box to get the message.
Читать дальше

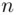 possible passwords in order to log on (or
possible passwords in order to log on (or 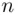 possible keys say), then how many guesses will we have to make on average until we are successful? The answer is easy to find .
possible keys say), then how many guesses will we have to make on average until we are successful? The answer is easy to find .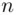 possible keys, we only need
possible keys, we only need 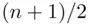 guesses.
guesses.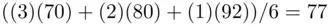 . So the average grade is 77%. We could also calculate the average as
. So the average grade is 77%. We could also calculate the average as 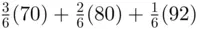 , where
, where 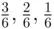 are the probabilities of getting 70, 80, and 92, respectively. Now, we proceed to the proof.
are the probabilities of getting 70, 80, and 92, respectively. Now, we proceed to the proof.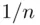 . To get it right in exactly 2 guesses, we must get it wrong on the first guess and then, having discarded the unsuccessful guess, we must guess correctly on the next attempt. So the probability of being successful in exactly 2 guesses is
. To get it right in exactly 2 guesses, we must get it wrong on the first guess and then, having discarded the unsuccessful guess, we must guess correctly on the next attempt. So the probability of being successful in exactly 2 guesses is 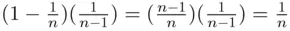 . Similarly, the probability of being successful in exactly
. Similarly, the probability of being successful in exactly 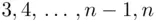 guesses is also
guesses is also 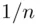 . To get the average number of guesses, we multiply the number of guesses by the probability and add up. This gives the average number of trials until success to be
. To get the average number of guesses, we multiply the number of guesses by the probability and add up. This gives the average number of trials until success to be 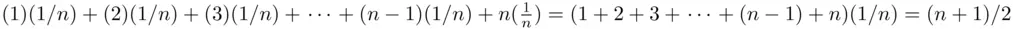 . So on average, you get the correct password after
. So on average, you get the correct password after 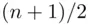 attempts.
attempts. (brute‐force). One of the main advantages of RSA is the convenience and low cost, especially for e‐commerce. Advantages of symmetric systems include improved security and the speed.
(brute‐force). One of the main advantages of RSA is the convenience and low cost, especially for e‐commerce. Advantages of symmetric systems include improved security and the speed. public!
public!










