The following is an analogy for symmetric encryption: If Awants to send a secret message to B, we can imagine Aputting the message in a strong box, locking the box with a key and mailing it to B. When Breceives the box, he opens it with his key and gets the message. Only Aand Bhave a key for the box, so nobody else can get the secret message.
3.6 Summary of Encryption
We have seen what encryption is and the difference between public key and symmetric cryptography. Public‐key algorithms such as RSA yield computational security which can be breached given sufficient time and computing resources. With RSA, security is weaker for a text message encoded in ASCII than if the message is a random binary string. This is also true for for some symmetric encryption systems. The reason for this reduction in security is attributed to the fact that consecutive characters in a text message are dependent upon each other.
The only mathematical way to assess the security of symmetric systems is through information theory, which is discussed later on in the book. The security depends on the uncertainty pertaining to the key and the uncertainty pertaining to the message. Roughly speaking, the longer the key the more secure the message. One reason for discussing historical ciphers, such as the Vigenère cipher, in this book is to furnish examples of how this works.
With public key algorithms, only one message can fit with a given cipher text. The keys have to be made longer and longer to withstand brute‐force attacks. What the proper length should be is a matter of conjecture and it is one of the “hot‐button” issues in modern cryptography. One the one hand, a financial institution using public key algorithms may not be in a hurry to report that its system has been broken. On the other hand, a successful intruder may not want to report success.
With symmetric systems, one can (at least in theory!) quantify the security which can be measured in Shannon bits . In certain situations, it can be measured exactly; in other situations, it can be estimated experimentally (e.g. with text messages encoded in binary). In general, it may be the case that many messages will fit with a given cipher text so that, in the end, the determination of the message may still be a matter of guesswork. Nowadays, RSA keys should be several hundred decimal digits in length. In bits, they should be at least 2048 bits long.
We should also point out that in some situations, whether dealing with symmetric or public key algorithms, it may be easier or faster to try to guess the message than to guess the key and then to get the message. Furthermore, there is a strong probabilistic component running through all of cryptography, exacerbated by the possibility of transmission errors.
We have not touched on several practical issues here such as message compression, transmission errors, and checking for key equality. These will be dealt with in Parts II and III of the book when the appropriate machinery has been built up.
3.7 The Diffie–Hellman Key Exchange
This is one of the most mathematically elegant algorithms in cryptography. Communicating parties 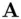 and
and 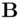 end up generating a common secret key, so there is a connection with symmetric encryption. On the other hand, the method of generating the common key is quite similar to the RSA algorithm and indeed is said to have inspired the RSA algorithm. The security of DH, like the security of RSA, is computational.
end up generating a common secret key, so there is a connection with symmetric encryption. On the other hand, the method of generating the common key is quite similar to the RSA algorithm and indeed is said to have inspired the RSA algorithm. The security of DH, like the security of RSA, is computational.
The DH key exchange may proceed in the following way:
Participants 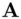 ,
, 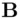 wish to generate a common secret key. First, a suitable prime
wish to generate a common secret key. First, a suitable prime 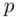 is publicly chosen and then a generator
is publicly chosen and then a generator 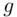 for
for 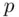 . Here, a generator
. Here, a generator 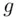 (which always exists!) has the property that if we take all powers of
(which always exists!) has the property that if we take all powers of 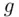 from 1 to
from 1 to 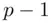 and calculate their remainders when we divide by
and calculate their remainders when we divide by 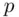 , we obtain all possible numbers
, we obtain all possible numbers  in some order (see Chapter 19). Recall that
in some order (see Chapter 19). Recall that 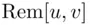 means the remainder when
means the remainder when 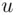 is divided by
is divided by 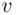 . Here, in this section, and in the problems,
. Here, in this section, and in the problems, 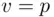 and
and 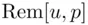 will be simply denoted by
will be simply denoted by 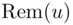 .
.
Procedure . 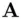 ,
, 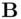 choose secret numbers
choose secret numbers 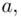
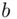 and transmit
and transmit 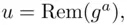
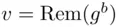 to
to 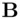 ,
, 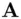 , respectively.
, respectively.
Читать дальше

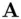 and
and 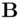 end up generating a common secret key, so there is a connection with symmetric encryption. On the other hand, the method of generating the common key is quite similar to the RSA algorithm and indeed is said to have inspired the RSA algorithm. The security of DH, like the security of RSA, is computational.
end up generating a common secret key, so there is a connection with symmetric encryption. On the other hand, the method of generating the common key is quite similar to the RSA algorithm and indeed is said to have inspired the RSA algorithm. The security of DH, like the security of RSA, is computational.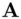 ,
, 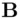 wish to generate a common secret key. First, a suitable prime
wish to generate a common secret key. First, a suitable prime 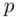 is publicly chosen and then a generator
is publicly chosen and then a generator 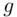 for
for 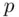 . Here, a generator
. Here, a generator 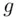 (which always exists!) has the property that if we take all powers of
(which always exists!) has the property that if we take all powers of 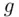 from 1 to
from 1 to 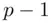 and calculate their remainders when we divide by
and calculate their remainders when we divide by 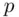 , we obtain all possible numbers
, we obtain all possible numbers  in some order (see Chapter 19). Recall that
in some order (see Chapter 19). Recall that 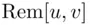 means the remainder when
means the remainder when 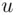 is divided by
is divided by 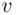 . Here, in this section, and in the problems,
. Here, in this section, and in the problems, 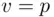 and
and 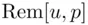 will be simply denoted by
will be simply denoted by 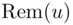 .
. ,
,  choose secret numbers
choose secret numbers 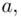
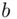 and transmit
and transmit 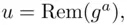
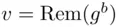 to
to  ,
,  , respectively.
, respectively.










