Aiden A. Bruen - Cryptography, Information Theory, and Error-Correction

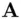wants to send a signed message 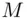to 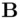. 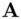begins with a large prime 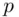and a generator 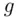(a primitive root) for that prime. Then 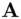chooses an integer such that 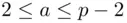. The public key of 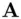is 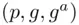and the private key of is 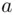. Since 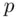and 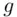are publicly known, it is important that it be infeasible to calculate the solution 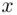to 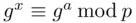. This requires that 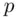have a large number of bits. When signing a message 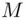, 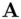chooses an integer 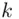relatively prime to such that . 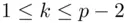Then 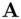transmits a signature in the form of the pair 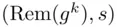, where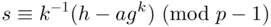

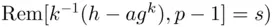
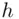(3.10)

(In other words,

and , the hash of the message 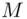, is some integer such that 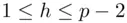. (The hash function maps strings of 0's and 1's onto the integer 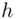in the proper range).

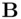The signature is verified by who checks the conditions:

1 The left integer in the signature pair, namely , lies in the interval .

2 The congruence is satisfied. In other words, we check that .

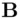If both conditions hold, then accepts the signature as coming from 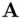. The reason for this is as follows: Substituting equation ( 3.10) into the second condition, we get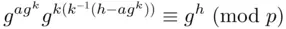

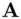(3.11)

This means that if computed 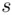, then condition 2 will be satisfied. Conversely, if condition 2 is satisfied, then (since 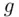is a primitive root of 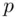) the exponents must give the same remainder on division by . Hence,

(3.12)

i.e.

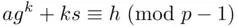
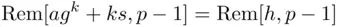
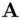which is a restatement of Eq. ( 3.10). So the computation carried out by is the only way to satisfy the second condition.