Vahid Mirjalili - Python Machine Learning

... lr.fit(X_train_std, y_train)

... weights.append(lr.coef_[1])

... params.append(10.**c)

>>> weights = np.array(weights)

>>> plt.plot(params, weights[:, 0],

... label='petal length')

>>> plt.plot(params, weights[:, 1], linestyle='--',

... label='petal width')

>>> plt.ylabel('weight coefficient')

>>> plt.xlabel('C')

>>> plt.legend(loc='upper left')

>>> plt.xscale('log')

>>> plt.show()

Si ejecutamos este código, ajustaremos diez modelos de regresión logística con distintos valores para el parámetro de regularización inverso C. A efectos de ilustración, solo hemos recogido los coeficientes de peso de la clase 1 (en este caso, la segunda clase en el conjunto de datos, Iris-versicolor) frente a todos los clasificadores –recuerda que estamos utilizando la técnica OvR para clasificación multiclase–.

Como podemos ver en el diagrama resultante, los coeficientes de peso se contraen si reducimos el parámetro C, es decir, si aumentamos la fuerza de regularización:

Como un tratamiento más profundo de los algoritmos de clasificación individual supera el objetivo de este libro, recomendamos fervientemente Logistic Regression: From Introductory to Advanced Concepts and Applications, Dr. Scott Menard's, Sage Publications, 2009, para aquellos lectores que deseen aprender más acerca de la regresión logística.

Margen de clasificación máximo con máquinas de vectores de soporte

Otro potente algoritmo de aprendizaje muy utilizado es la máquina de vectores de soporte (SVM, del inglés Support Vector Machine), que puede considerarse una extensión del perceptrón. Con el algoritmo del perceptrón, minimizamos errores de clasificación. Sin embargo, con las SVM nuestro objetivo de optimización es maximizar el margen. El margen se define como la distancia entre el hiperplano de separación (límite de decisión) y las muestras de entrenamiento que están más cerca de ese hiperplano, que también se denominan vectores de soporte. Así lo mostramos en la siguiente imagen:

Margen máximo de intuición

El razonamiento que hay detrás de tener límites de decisión con amplios márgenes es que estos tienden a tener más bajo error de generalización allí donde los modelos con márgenes pequeños son más propensos al sobreajuste. Para hacernos una idea de la maximización del margen, echaremos un vistazo a aquellos hiperplanos positivos y negativos que son paralelos al límite de decisión, que puede expresarse así:

Si restamos las dos ecuaciones lineales (1) y (2) entre ellas, obtenemos:

Podemos normalizar esta ecuación mediante la longitud del vector w, que se define del siguiente modo:

De este modo, llegamos a la siguiente ecuación:

La parte izquierda de la ecuación anterior puede ser interpretada como la distancia entre el hiperplano positivo y el negativo, también denominada margen, que queremos maximizar.

Ahora, la función objetiva de la SVM pasa a ser la maximización de este margen, maximizando bajo la restricción de que las muestras están clasificadas correctamente. Puede escribirse así:

En este caso, N es el número de muestra de nuestro conjunto de datos.

Estas dos ecuaciones dicen básicamente que todas las muestras negativas deben caer en un lado del hiperplano negativo, mientras que todas las muestras positivas deben caer detrás del hiperplano positivo. Puede escribirse de manera compacta del siguiente modo:

En la práctica, sin embargo, es más sencillo minimizar el término recíproco , que se puede resolver mediante programación cuadrática. Ahora bien, como el tratamiento más detallado de la programación cuadrática queda fuera del objetivo de este libro, puedes aprender más sobre las máquinas de vectores de soporte en The Nature of Statistical Learning Theory, Springer Science+Business Media, Vladimir Vapnik (2000), o bien en la excelente explicación de Chris J.C. Burges en A Tutorial on Support Vector Machines for Pattern Recognition (Data Mining and Knowledge Discovery, 2(2): 121-167, 1998).

Tratar un caso separable no lineal con variables flexibles

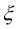Aunque no queremos llegar mucho más lejos en los conceptos matemáticos que se esconden detrás del margen máximo de clasificación, sí que mencionaremos brevemente la variable flexible , que presentó Vladimir Vapnik en 1995 y dio lugar a la denominada clasificación de margen blando. La motivación para introducir la variable flexible es que las restricciones lineales deben ser relajadas para los datos separables no lineales para permitir la convergencia de la optimización cuando existen errores de clasificación, bajo la penalización de coste apropiada.