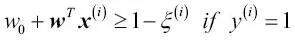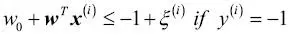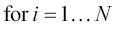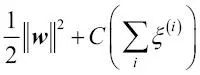Vahid Mirjalili - Python Machine Learning

La variable flexible de valores positivos simplemente se añade a las restricciones lineales:

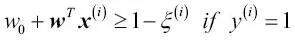
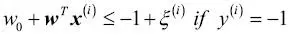
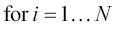
En este caso, N es el número de muestras en nuestro conjunto de datos. Así, el nuevo objetivo que se debe minimizar (sujeto a las restricciones) pasa a ser:

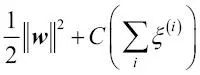
Mediante la variable C, podemos controlar la penalización por error de clasificación. Si C cuenta con valores amplios se producirán amplias penalizaciones de errores, mientras que si elegimos para C valores más pequeños seremos menos estrictos con los errores de clasificación. También podemos utilizar el parámetro C para controlar la anchura del margen y, así, afinar la compensación entre el sesgo y la varianza, como se muestra en la siguiente imagen:

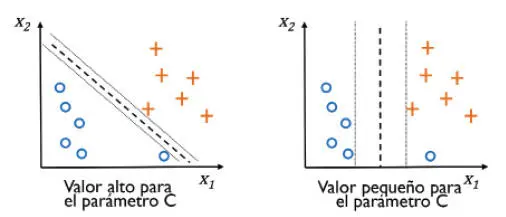
Este concepto está relacionado con la regularización, que tratamos en la sección anterior cuando hablamos de que la regresión regularizada, al reducir el valor de C, aumenta el sesgo y disminuye la varianza del modelo.

Ahora que hemos aprendido los conceptos básicos de las SVM lineales, vamos a entrenar un modelo de SVM para clasificar las distintas flores en nuestro conjunto de datos Iris:

>>> from sklearn.svm import SVC

>>> svm = SVC(kernel='linear', C=1.0, random_state=1)

>>> svm.fit(X_train_std, y_train)

>>> plot_decision_regions(X_combined_std,

... y_combined,

... classifier=svm,

... test_idx=range(105, 150))

>>> plt.xlabel('petal length [standardized]')

>>> plt.ylabel('petal width [standardized]')

>>> plt.legend(loc='upper left')

>>> plt.show()

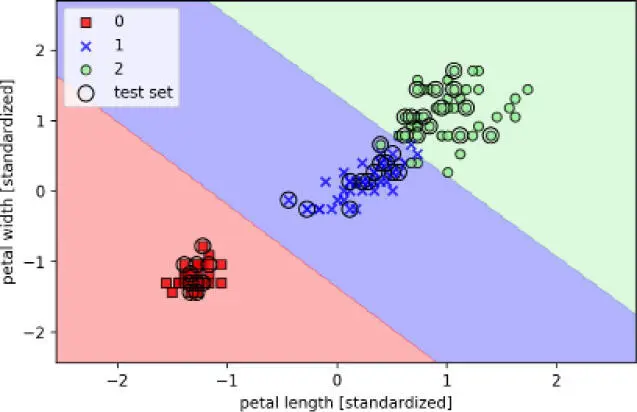
Las tres regiones de decisión de la SVM, que mostramos después de entrenar el clasificador en el conjunto de datos Iris mediante la ejecución del código de ejemplo, se muestran en el siguiente diagrama:

Regresión logística frente a las máquinas de vectores de soporteEn las tareas de clasificación prácticas, la regresión logística lineal y las SVM lineales a menudo proporcionan resultados muy parecidos. La regresión logística intenta maximizar las probabilidades condicionales de los datos de entrenamiento, y los hace más propensos a valores extremos o outliers que las SVM, que tienen en cuenta sobre todo los puntos más cercanos al límite de decisión (vectores de soporte). Por otro lado, la regresión logística tiene la ventaja de ser un modelo más simple y de poder implementarse más fácilmente. Además, los modelos de regresión logística pueden ser actualizados con facilidad, lo cual es un factor atractivo si se trabaja con transmisión de datos.

Implementaciones alternativas en scikit-learn

La librería Perceptron y las clases LogisticRegression de scikit-learn, que hemos utilizado en la sección anterior, hacen uso de la librería LIBLINEAR, que es una librería C/C++ altamente optimizada desarrollada en la National Taiwan University (http://www.csie.ntu.edu.tw/~cjlin/liblinear/). De forma parecida, la clase SVC, que utilizamos para entrenar un SVM, hace uso de LIBSVM, que es una librería C/C++ equivalente especializada para SVM (http://www.csie.ntu.edu.tw/~cjlin/libsvm/).

La ventaja de utilizar LIBLINEAR y LIBSVM sobre implementaciones nativas de Python es que permiten un entrenamiento extremadamente rápido de grandes cantidades de clasificadores lineales. Sin embargo, a veces nuestros conjuntos de datos son demasiado grandes para encajarlos en las memorias de los ordenadores. Por esta razón, scikit-learn también ofrece implementaciones alternativas mediante la clase SGDClassifier, que también soporta aprendizaje online a través del método partial_fit. El concepto que se esconde detrás de la clase SGDClassifier es similar al algoritmo de gradiente estocástico que implementamos en el Capítulo 2, Entrenar algoritmos simples de aprendizaje automático para clasificación para Adaline. Podríamos inicializar la versión del descenso del gradiente estocástico, una regresión logística y una máquina de vectores de soporte con parámetros predeterminados de la siguiente forma:

>>> from sklearn.linear_model import SGDClassifier

>>> ppn = SGDClassifier(loss='perceptron')

>>> lr = SGDClassifier(loss='log')

>>> svm = SGDClassifier(loss='hinge')

Resolver problemas no lineales con una SVM kernelizada

Otra razón por la cual las SVM gozan de gran popularidad entre los que trabajan con el aprendizaje automático es que pueden ser fácilmente kernelizadas para resolver problemas de clasificación no lineal. Antes de tratar el concepto principal que se esconde detrás de una SVM kernelizada, vamos primero a crear un conjunto de datos de muestra para ver qué aspecto tendría un problema de clasificación no lineal.

Métodos kernel para datos inseparables lineales

Con el siguiente código, crearemos un sencillo conjunto de datos que tiene la forma de una puerta XOR mediante la función logical_or de NumPy, donde se asignarán 100 muestras a la etiqueta de clase 1 y otras 100 a la etiqueta de clase -1:

>>> import matplotlib.pyplot as plt

>>> import numpy as np

>>> np.random.seed(1)

>>> X_xor = np.random.randn(200, 2)

>>> y_xor = np.logical_xor(X_xor[:, 0] > 0,

... X_xor[:, 1] > 0)

>>> y_xor = np.where(y_xor, 1, -1)

>>> plt.scatter(X_xor[y_xor == 1, 0],

... X_xor[y_xor == 1, 1],

... c='b', marker='x',

... label='1')

>>> plt.scatter(X_xor[y_xor == -1, 0],

... X_xor[y_xor == -1, 1],

... c='r',

... marker='s',

... label='-1')

>>> plt.xlim([-3, 3])

>>> plt.ylim([-3, 3])

>>> plt.legend(loc='best')

>>> plt.show()

Después de ejecutar el código, tendremos un conjunto de datos XOR con ruido aleatorio, como se muestra en la siguiente imagen:

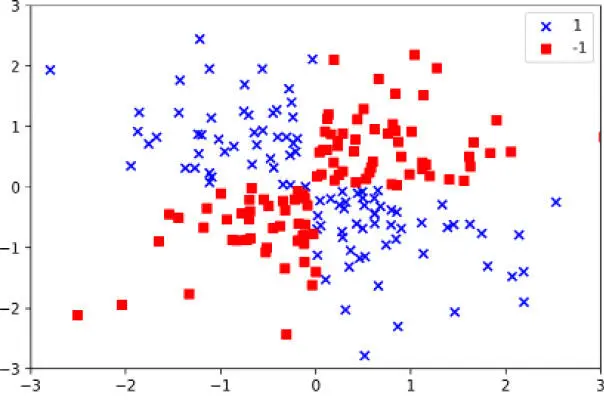
Evidentemente, no podríamos separar correctamente las muestras de las clases positivas y negativas utilizando un hiperplano lineal como límite de decisión a través de la regresión logística lineal o del modelo de SVM lineal que tratamos en secciones anteriores.