La primera fila corresponde a las probabilidades de pertenencia a una clase de la primera flor, la segunda fila corresponde a las probabilidades de pertenencia a una clase de la tercera flor, etc. Observa que las columnas suman todas más de uno, como esperábamos (puedes confirmar este hecho ejecutando lr.predict_proba(X_test_std[:3, :]).sum(axis=1)). El valor más alto de la primera fila es aproximadamente 0.853, lo cual significa que la primera muestra pertenece a la clase tres (Iris-virginica) con una predicción de la probabilidad del 85.7 %. Así, como ya habrás observado, podemos obtener las etiquetas de clase predichas identificando la columna más grande de cada fila; por ejemplo, mediante la función argmax de NumPy:
>>> lr.predict_proba(X_test_std[:3, :]).argmax(axis=1)
Los índices de clase devueltos se muestran a continuación (estos corresponden a Iris-virginica, Iris-setosa e Iris-setosa):
array([2, 0, 0])
Las etiquetas de clase que obtuvimos a partir de las probabilidades condicionales anteriores son, evidentemente, solo un enfoque manual para llamar directamente al método predict, que podemos verificar de la siguiente manera:
>>> lr.predict(X_test_std[:3, :])
array([2, 0, 0])
Por último, una advertencia si quieres predecir la etiqueta de clase de una única muestra de flor: scikit-learn espera una matriz bidimensional como entrada de datos; por tanto, debemos convertir primero una fila única a un formato de este tipo. Una manera de convertir una entrada de fila única en una matriz de datos bidimensional es utilizando el método reshape de NumPy para añadir una nueva dimensión, como se demuestra a continuación:
>>> lr.predict(X_test_std[0, :].reshape(1, -1))
array([2])
Abordar el sobreajuste con la regularización
El sobreajuste es un problema común en el aprendizaje automático, donde un modelo funciona bien en el entrenamiento de datos pero no generaliza bien con los datos no vistos (datos de prueba). Si un modelo sufre una situación de sobreajuste, también decimos que el modelo tiene una alta varianza, causada quizás por tener demasiados parámetros que conducen a un modelo demasiado complejo dados los datos subyacentes. De forma parecida, nuestro modelo también puede sufrir una situación de subajuste o underfitting (un sesgo elevado), que significa que nuestro modelo no es suficientemente complejo como para capturar correctamente el patrón en los datos de entrenamiento y, por lo tanto, sufre por el bajo rendimiento en los datos no vistos.
Aunque hasta ahora solo hemos encontrado modelos lineales para clasificación, el problema del sobreajuste y el subajuste se puede ilustrar mejor mediante la comparación de un límite de decisión lineal con otros límites de decisión no lineales y más complejos, como se muestra en la siguiente imagen:
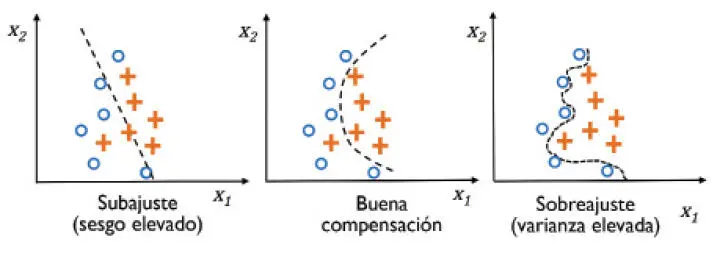
 |
 |
La varianza mide la consistencia (o variabilidad) de la predicción del modelo para una instancia de muestra en particular en el caso de tener que entrenar el modelo varias veces, por ejemplo en diferentes subconjuntos del conjunto de datos de entrenamiento. Podemos decir que el modelo es sensible a la aleatoriedad en los datos de entrenamiento. Al contrario, el sesgo mide cómo estarían de lejos las predicciones de los valores correctos si volviéramos a crear el modelo varias veces en distintos conjuntos de datos de entrenamiento; el sesgo es la medida del error sistemático que no procede de la aleatoriedad. |
 |
Una manera de encontrar una buena compensación entre el sesgo y la varianza es afinar la complejidad del modelo mediante la regularización. La regularización es un método muy útil para manejar la colinealidad (alta correlación entre características), filtra el ruido de los datos y puede prevenir el sobreajuste. El concepto que hay detrás de la regularización es presentar información adicional (sesgo) para penalizar valores (peso) de parámetros extremos. La forma más común de regularización también se denomina regularización L2 (conocida a veces como contracción L2 o penalización de pesos), que puede escribirse de la siguiente forma:
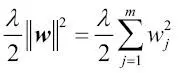
Aquí, 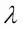 también se denomina parámetro de regularización.
también se denomina parámetro de regularización.
 |
 |
La regularización es otra de las razones por las que el escalado de características como la normalización es importante. Para que la regularización funcione adecuadamente, debemos asegurarnos de que todas nuestras características se encuentran en escalas comparables. |
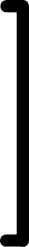 |
La función de coste para la regresión logística se puede regularizar añadiendo un sencillo término de regularización, que contraerá los pesos durante el entrenamiento del modelo:
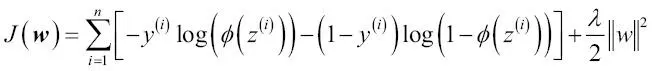
Mediante el parámetro de regularización  , podemos controlar el ajuste de los datos de entrenamiento manteniendo pequeños los pesos. Si aumentamos el valor de
, podemos controlar el ajuste de los datos de entrenamiento manteniendo pequeños los pesos. Si aumentamos el valor de  , aumentamos la fuerza de regularización.
, aumentamos la fuerza de regularización.
El parámetro C implementado para la clase LogisticRegression en scikit-learn procede de una convención entre las máquinas de vectores de soporte, tema que será tratado en la siguiente sección. El término C está directamente relacionado con el parámetro de regularización 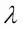 , que es su inverso. En consecuencia, reducir el valor del parámetro de regularización inverso C significa que estamos incrementando la fuerza de regularización, hecho que podemos visualizar mostrando gráficamente la ruta de regularización L2 para los dos coeficientes de peso:
, que es su inverso. En consecuencia, reducir el valor del parámetro de regularización inverso C significa que estamos incrementando la fuerza de regularización, hecho que podemos visualizar mostrando gráficamente la ruta de regularización L2 para los dos coeficientes de peso:
>>> weights, params = [], []
>>> for c in np.arange(-5, 5):
... lr = LogisticRegression(C=10.**c, random_state=1)
Читать дальше


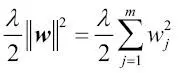
 también se denomina parámetro de regularización.
también se denomina parámetro de regularización.
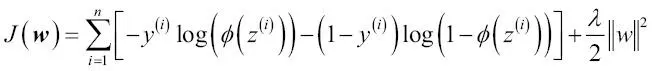
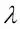 , podemos controlar el ajuste de los datos de entrenamiento manteniendo pequeños los pesos. Si aumentamos el valor de
, podemos controlar el ajuste de los datos de entrenamiento manteniendo pequeños los pesos. Si aumentamos el valor de 










