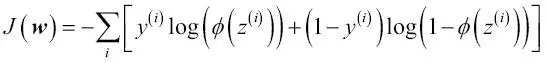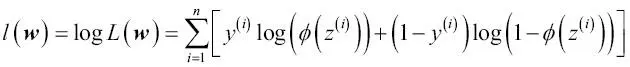
En primer lugar, la aplicación de la función log reduce el potencial para el desbordamiento numérico, que puede ocurrir si las probabilidades son muy pequeñas. En segundo lugar, podemos convertir el producto de factores en una suma de factores, que hace más fácil obtener la derivada de esta función mediante el truco de la suma, como recordarás del cálculo.
Ahora, podríamos utilizar un algoritmo de optimización como el ascenso del gradiente para maximizar esta función de probabilidad logarítmica. De forma alternativa, vamos a volver a escribir la probabilidad logarítmica como una función de coste J que puede ser minimizada mediante el descenso del gradiente, como en el Capítulo 2, Entrenar algoritmos simples de aprendizaje automático para clasificación:
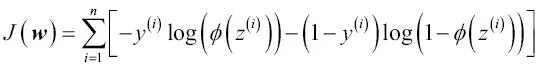
Para entender mejor esta función de coste, echemos un vistazo al coste que calculamos para una instancia de entrenamiento de muestra única:
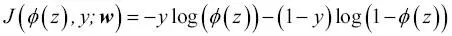
Si miramos la ecuación, podemos ver que el primer término es cero si 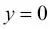 , y que el segundo término es cero si
, y que el segundo término es cero si 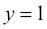 :
:
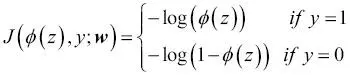
Vamos a escribir un pequeño fragmento de código para crear un diagrama que ilustre el coste de la clasificación de una instancia de muestra única para diferentes valores de 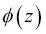 :
:
>>> def cost_1(z):
... return - np.log(sigmoid(z))
>>> def cost_0(z):
... return - np.log(1 - sigmoid(z))
>>> z = np.arange(-10, 10, 0.1)
>>> phi_z = sigmoid(z)
>>> c1 = [cost_1(x) for x in z]
>>> plt.plot(phi_z, c1, label='J(w) if y=1')
>>> c0 = [cost_0(x) for x in z]
>>> plt.plot(phi_z, c0, linestyle='--', label='J(w) if y=0')
>>> plt.ylim(0.0, 5.1)
>>> plt.xlim([0, 1])
>>> plt.xlabel('$\phi$(z)')
>>> plt.ylabel('J(w)')
>>> plt.legend(loc='best')
>>> plt.show()
El diagrama resultante muestra la activación sigmoide en el eje x en el rango de 0 a 1 (las entradas en la función sigmoide eran valores z en el rango de -10 a 10) y el coste logístico asociado en el eje y:
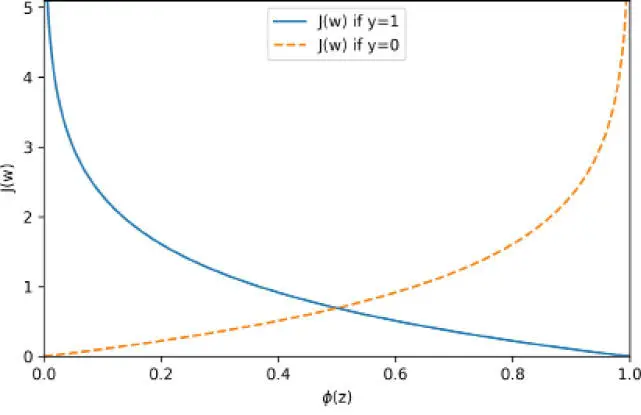
Podemos ver que el coste se acerca a 0 (línea continua) si predecimos correctamente que una muestra pertenece a la clase 1. De forma similar, podemos ver en el eje y que el coste también se acerca a 0 si predecimos correctamente 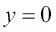 (línea discontinua). Sin embargo, si la predicción es errónea, el coste se dirige hacia el infinito. La conclusión principal es que penalizamos las predicciones erróneas con un coste cada vez mayor.
(línea discontinua). Sin embargo, si la predicción es errónea, el coste se dirige hacia el infinito. La conclusión principal es que penalizamos las predicciones erróneas con un coste cada vez mayor.
Convertir una implementación Adaline en un algoritmo para regresión logística
Si debemos implementar nosotros mismos una regresión logística, sencillamente podemos sustituir la función de coste J en nuestra implementación Adaline del Capítulo 2, Entrenar algoritmos simples de aprendizaje automático para clasificación con la nueva función de coste:
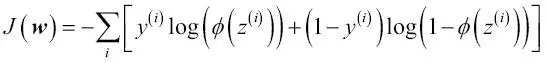
Utilizamos este proceso para calcular el coste de clasificar todas las muestras de entrenamiento por época. Además, tenemos que intercambiar la función de activación lineal por la activación sigmoide y cambiar la función umbral para devolver etiquetas de clase 0 y 1 en lugar de -1 y 1. Si realizamos estos tres cambios en el código de Adaline, conseguiremos una implementación de regresión logística que funciona, como se muestra a continuación:
class LogisticRegressionGD(object):
"""Logistic Regression Classifier using gradient descent.
Parameters
------------
eta : float
Learning rate (between 0.0 and 1.0)
n_iter : int
Passes over the training dataset.
random_state : int
Random number generator seed for random weight
initialization.
Attributes
-----------
w_ : 1d-array
Weights after fitting.
cost_ : list
Sum-of-squares cost function value in each epoch.
"""
def __init__(self, eta=0.05, n_iter=100, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
""" Fit training data.
Parameters
----------
X : {array-like}, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of
samples and
n_features is the number of features.
y : array-like, shape = [n_samples]
Target values.
Returns
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01,
size=1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
# note that we compute the logistic `cost` now
# instead of the sum of squared errors cost
cost = (-y.dot(np.log(output)) -
((1 - y).dot(np.log(1 - output))))
self.cost_.append(cost)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, z):
"""Compute logistic sigmoid activation"""
return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.net_input(X) >= 0.0, 1, 0)
# equivalente a:
# return np.where(self.activation(self.net_input(X))
# >= 0.5, 1, 0)
Cuando configuramos un modelo de regresión logística, debemos tener en cuenta que este solo funciona para tareas de clasificación binaria. Así, vamos a considerar solo las flores Iris-setosa e Iris-versicolor (clases 0 y 1) y a comprobar que nuestra implementación de regresión logística funciona:
>>> X_train_01_subset = X_train[(y_train == 0) | (y_train == 1)]
>>> y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]
>>> lrgd = LogisticRegressionGD(eta=0.05,
Читать дальше

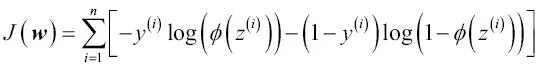
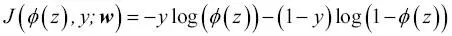
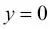 , y que el segundo término es cero si
, y que el segundo término es cero si 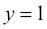 :
: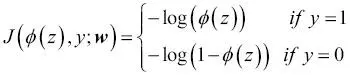
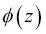 :
:
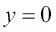 (línea discontinua). Sin embargo, si la predicción es errónea, el coste se dirige hacia el infinito. La conclusión principal es que penalizamos las predicciones erróneas con un coste cada vez mayor.
(línea discontinua). Sin embargo, si la predicción es errónea, el coste se dirige hacia el infinito. La conclusión principal es que penalizamos las predicciones erróneas con un coste cada vez mayor.