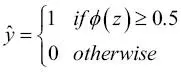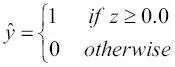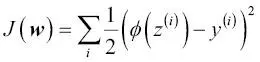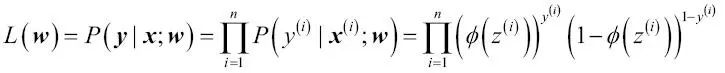Vahid Mirjalili - Python Machine Learning
Здесь есть возможность читать онлайн «Vahid Mirjalili - Python Machine Learning» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на испанском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Python Machine Learning
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Python Machine Learning: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Python Machine Learning»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Modernizado y ampliado para incluir las tecnologías de código abierto más recientes, como scikit-learn, Keras y TensorFlow, este manual proporciona el conocimiento práctico y las técnicas necesarias para crear eficaces aplicaciones de aprendizaje automático y aprendizaje profundo en Python.
El conocimiento y la experiencia únicos de Sebastian Raschka y Vahid Mirjalili presentan los algoritmos de aprendizaje automático y aprendizaje profundo, antes de continuar con temas avanzados en análisis de datos.
Combinan los principios teóricos del aprendizaje automático con un enfoque práctico de codificación para una comprensión completa de la teoría del aprendizaje automático y la implementación con Python.
Aprenderás a:
Explorar y entender los frameworks clave para la ciencia de datos, el aprendizaje automático y el aprendizaje profundo
Formular nuevas preguntas sobre datos con modelos de aprendizaje automático y redes neuronales
Aprovechar el poder de las últimas librerías de código abierto de Python para aprendizaje automático
Dominar la implementación de redes neuronales profundas con la librería de TensorFlow
Incrustar modelos de aprendizaje automáticos en aplicacions web accesibles
Predecir resultados objetivos continuos con análisis de regresión
Descubrir patrones ocultos y estructuras en datos con agrupamientos
Analizar imágenes mediante técnicas de aprendizaje profundo
Profundizar en datos de medios sociales y textuales con el análisis de sentimientos

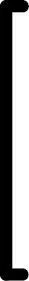

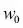 se refiere al parámetro del sesgo y es un valor de entrada adicional que proporcionamos (
se refiere al parámetro del sesgo y es un valor de entrada adicional que proporcionamos ( 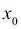 ) que es igual a 1.
) que es igual a 1.
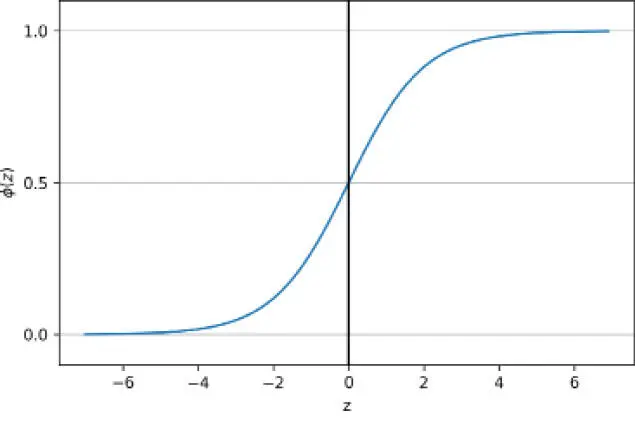
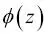 se acerca a 1 si z se dirige hacia el infinito (
se acerca a 1 si z se dirige hacia el infinito ( 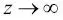 ), puesto que
), puesto que 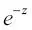 pasa a ser muy pequeño para los amplios valores de z. De forma parecida,
pasa a ser muy pequeño para los amplios valores de z. De forma parecida, 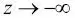 como resultado de un denominador cada vez más grande. Así, llegamos a la conclusión de que la función sigmoide toma valores de números reales como entrada y los transforma en valores del rango [0, 1] con una intercepción en
como resultado de un denominador cada vez más grande. Así, llegamos a la conclusión de que la función sigmoide toma valores de números reales como entrada y los transforma en valores del rango [0, 1] con una intercepción en 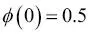 .
.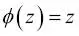 como función de activación. En regresión lógica, esta función de activación simplemente se convierte en la función sigmoide que hemos definido anteriormente. La diferencia entre Adaline y la regresión logística se muestra en la siguiente imagen:
como función de activación. En regresión lógica, esta función de activación simplemente se convierte en la función sigmoide que hemos definido anteriormente. La diferencia entre Adaline y la regresión logística se muestra en la siguiente imagen: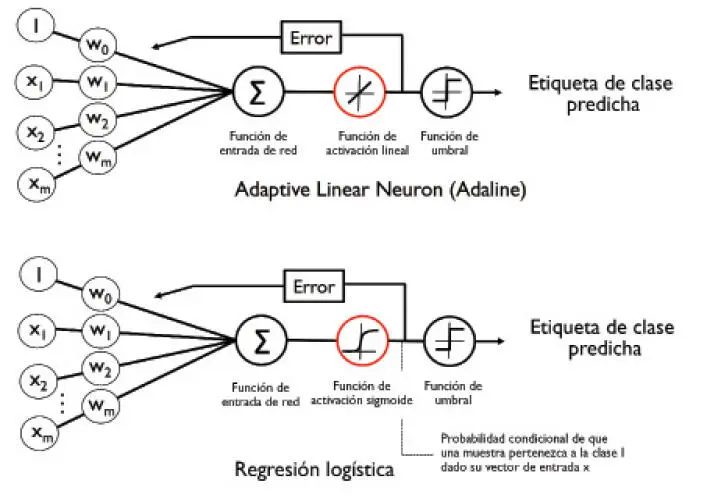
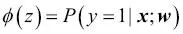 , dadas sus características x parametrizadas por los pesos w. Por ejemplo, si calculamos
, dadas sus características x parametrizadas por los pesos w. Por ejemplo, si calculamos 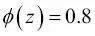 para una muestra de flor en particular, significa que la oportunidad de que esta muestra sea una flor Iris-versicolor es del 0 %. Por lo tanto, la probabilidad de que esta flor sea una Iris-setosa se puede calcular como
para una muestra de flor en particular, significa que la oportunidad de que esta muestra sea una flor Iris-versicolor es del 0 %. Por lo tanto, la probabilidad de que esta flor sea una Iris-setosa se puede calcular como 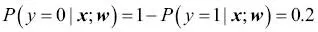 o 20 %. La probabilidad predicha se puede, simplemente, convertir después en un resultado binario mediante una función umbral:
o 20 %. La probabilidad predicha se puede, simplemente, convertir después en un resultado binario mediante una función umbral: