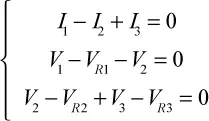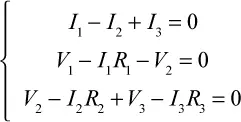Paolo Aliverti - Electrónica. Trucos y secretos

− I 1+ I 2− I 3= 0

Nuestro circuito tiene, por consiguiente, tres incógnitas en total, que equivalen a las tres corrientes, I 1, I 2e I 3. Para determinar sus valores, debo recoger como mínimo tres ecuaciones. Si las ecuaciones para el nodo A y B son prácticamente idénticas, puedo escribir un sistema que utilice solo tres de las ecuaciones que hemos escrito, y elijo estas:

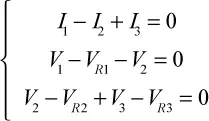
Utilizando la ley de Ohm, puedo volver a escribir las últimas dos ecuaciones sustituyendo la tensión en los extremos de las resistencias y haciendo que aparezcan las corrientes:

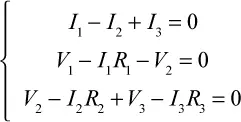
Al resolver el sistema, obtengo los valores para I 1, I 2e I 3y, por tanto, puedo conocer todas las magnitudes eléctricas dentro de mi circuito.

Saber generar las ecuaciones y desarrollar los cálculos es importante y no habría que perder nunca la práctica; sin embargo, en las tareas cotidianas o para tener una respuesta rápida y segura, es mejor confiar en un simulador de circuitos.

A veces puede que tengamos que enfrentarnos a un circuito muy complejo, tanto que requiera un elevado número de ecuaciones para su resolución (con Kirchhoff). El teorema de Thevenin nos puede ayudar a resolver estos casos intrincados siempre que el circuito que hay que examinar esté formado por resistores y generadores de tensión y de corriente. El concepto básico es considerar dos terminales del circuito y pensar que todo el circuito, por complejo que sea, se puede resumir en una especie de caja negra (black box) con dos simples terminales. Detrás de estos dos terminales encontramos simplemente una resistencia y un generador de tensión equivalentes que resumen el comportamiento de toda la red. Los terminales que elijamos son, obviamente, los que nos interesan, por ejemplo, un punto concreto acerca del cual deseamos conocer la tensión y la corriente presentes. A menudo estos dos puntos son los terminales de un componente presente. En este caso, tendremos que eliminar (ideal o realmente) el componente para obtener el equivalente de Thevenin del circuito existente. El teorema de Thevenin prevé dos fases:

1. en primer lugar se mide la tensión presente en los terminales del circuito;

2. en una segunda fase se eliminan los generadores y se sustituyen con circuitos abiertos o cortocircuitos, y se calcula la resistencia equivalente.

Consideremos el circuito que se muestra en la figura 1.18, formado por una red con varios generadores. El circuito no presenta realmente terminales y nos interesa medir tensión y corriente en los extremos de la resistencia Rx. Por esta razón, eliminamos la resistencia y la consideramos como una carga que conectaremos más tarde.

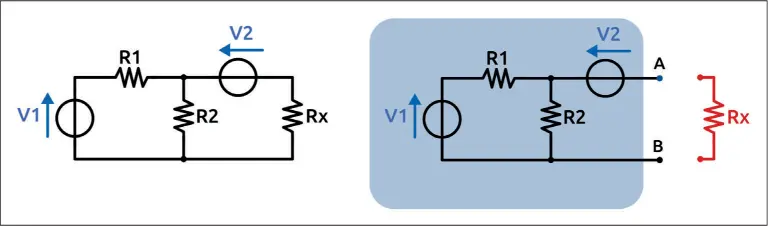
Figura 1.18– Circuito de ejemplo para calcular el equivalente de Thevenin. A la derecha observamos el circuito al cual se ha eliminado la resistencia Rx.

Una vez eliminada la resistencia, hemos obtenido los dos terminales, A y B ( figura 1.18) a los cuales llega el resto de la red que consideramos como una caja negra. Como hemos dicho, para resolver el circuito en los terminales A-B previamente debemos extraer la tensión existente en los terminales. Podemos utilizar a Kirchhoff para obtener la tensión presente entre A y B.

La tensión entre A y B es la tensión equivalente de Thevenin. Pasemos a calcular la resistencia equivalente modificando el circuito de este modo:

• sustituyendo con un cortocircuito los generadores de tensión;

• eliminando los generadores de corriente (sustitución con circuito abierto).

Una vez hemos sustituido los generadores presentes, podemos calcular el valor de la resistencia equivalente de Thevenin, es decir, la resistencia visible en los terminales A y B.

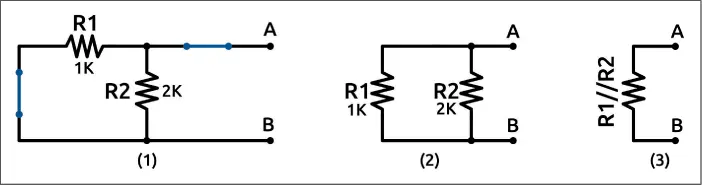
Figura 1.19– El circuito modificado con los generadores de tensión cortocircuitados.

Ahora podemos dibujar el circuito equivalente de Thevenin formado por la resistencia R eqen serie con el generador de tensión V eq( figura 1.20).

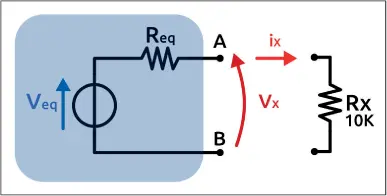
Figura 1.20– El circuito equivalente de Thevenin al cual conectamos la Rx.

Al volver a conectar la resistencia Rx que hemos desconectado al inicio, podemos realizar los cálculos necesarios para determinar la corriente que pasa por ella y la tensión que medimos en sus extremos.

Existe una versión dual del teorema de Thevenin denominada teorema de Norton, según la cual, con un procedimiento idéntico al mostrado, es posible obtener una versión equivalente de un circuito formado por resistencias y generadores de tensión y corriente con un simple generador de corriente con una resistencia equivalente en paralelo. En este caso, es necesario identificar dos terminales y extraer la corriente que se obtendría cortocircuitándolos. Después hay que determinar la resistencia equivalente que se puede calcular cortocircuitando los generadores de tensión y eliminando todos los generadores de corriente.

En electrónica y electrotécnica a menudo se trabaja con conceptos matemáticos que pueden no ser demasiado sencillos. Para entender y estudiar algunos argumentos, se necesita algún conocimiento de análisis matemático y, por tanto, de algunos instrumentos que se explican normalmente en los últimos cursos de instituto o en la universidad.

No pretendo transmitir aquí todo el conocimiento matemático necesario para afrontar cálculos complejos de análisis, pero sí me gustaría darles algunos conceptos fundamentales para entender algunas de las fórmulas con que nos encontraremos. Todas las magnitudes electrónicas pueden ser expresadas con una regla que trata de explicar cómo se comportan. Normalmente, en matemáticas, estas reglas se conocen con el nombre de funciones, un concepto que la mayoría ya debieran conocer. Podemos imaginarnos una función como una caja mágica que toma un número a la entrada y proporciona un número a la salida. El número proporcionado a la entrada, también denominado variable de entrada, normalmente se indica con una x, mientras que el resultado se indica con la letra y.

Podemos indicar una función genérica así:

y = f ( x )

Con este término no estamos diciendo mucho, solo que la variable y está determinada por una operación matemática aplicada a la x. Estas operaciones genéricas se indican con la letra f.

Podemos ser más precisos y tratar de describir el comportamiento de la función añadiendo términos que trabajan sobre la variable x inmediatamente después del signo =. Este es un ejemplo de función matemática:

y = 12 · x 2+ 10 · x − 8

También podemos trazar sobre un gráfico la función para estudiar su tendencia. En electrónica, las funciones dependen a menudo del tiempo y de la frecuencia. Por tanto, encontraremos textos similares a este: