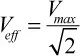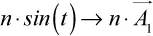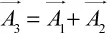El último parámetro de nuestra sinusoide es la fase (ϕ) 3 , necesaria en el caso en que se desee que la onda empiece en un punto distinto a 0.
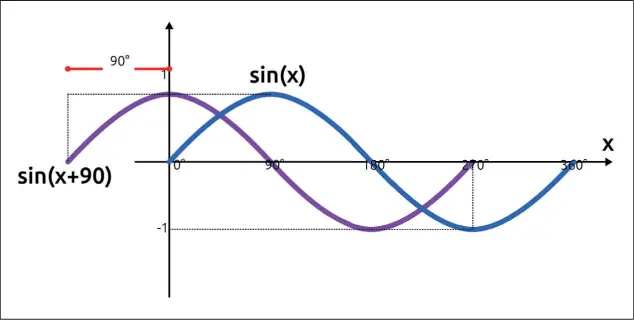
Figura 1.23– Efecto de la fase sobre la sinusoide.
Cuando se estudian circuitos donde circulan corrientes sinusoidales, puede resultar cómodo utilizar una descripción alternativa y más práctica para realizar los cálculos en lugar de tratar directamente con las sinusoides. Al aplicar una señal a una determinada frecuencia a un circuito formado por componentes comunes (resistencias, inductancias, condensadores), todas las magnitudes eléctricas presentes cambiarán con la misma pulsación (a la misma frecuencia). En estos casos puedo simplificar las cosas y mantener solo lo indispensable. Considero una onda cosinusoidal (simplifico los cálculos a continuación):
v ( t ) = A · cos (2π ft + φ )
de la cual solo me ocupo de:
A , φ
porque la frecuencia será la misma para todo el circuito. Estos dos números expresan una amplitud y un ángulo y pueden dibujarlos sobre un gráfico. Estamos acostumbrados a utilizar gráficos cartesianos, donde las coordenadas se indican sobre dos ejes perpendiculares entre sí. Un modo alternativo de indicar un punto es mediante las coordinadas polares, que especifican, en lugar de la x y la y, la distancia del punto de partida y el ángulo de inclinación respecto a un eje de referencia.
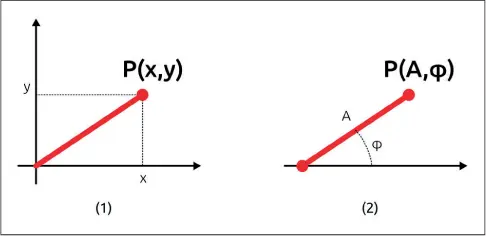
Figura 1.24– Coordenadas rectangulares (1) y polares (2).
Obviamente, siempre se puede pasar de un sistema de coordenadas al otro mediante algún cálculo (necesitarán una calculadora científica, un seno y un coseno). Por ahora no necesitamos realizar ningún paso de coordenadas, por lo que seguiremos adelante... Sabemos indicar las coordenadas de un punto en el plano cartesiano y podemos hacerlo escribiendo, por ejemplo, las coordenadas entre paréntesis, separadas por comas:
P = ( a,b )
Con las coordenadas polares, podemos hacer algo parecido a esto:
P = ( A , φ )
Los primeros matemáticos e ingenieros que estudiaron estas señales prefirieron utilizar una versión mucho más elegante que el simple espacio cartesiano formado por dos coordenadas, x e y, y adoptaron aquello que se conoce como números complejos (o imaginarios), que permiten combinar x e y en un único número (disculpen la definición poco precisa y algo folclórica). Así, podemos indicar el mismo punto P de esta forma:
P = a + jb
La j que vemos antes de la b es la unidad imaginaria que, a veces, también se indica con una i. Podemos dibujar en un gráfico cartesiano este número como si fuera un punto común con una abscisa (la x) que equivale a la a, y una ordenada (la y) que equivale a la b. Podemos transformar un número imaginario en su representación polar. Tampoco en este caso tendremos dos números desvinculados, sino que podemos escribir el conjunto de un modo más compacto:
P = A · e jφ
A es igual a la longitud del segmento que une el origen con el punto, mientras que ϕ es la inclinación del segmento respecto al eje horizontal.
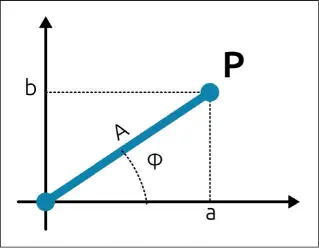
Figura 1.25– El punto P representado en el plano imaginario, en coordenadas cartesianas y polares.
Hemos partido de una sinusoide para llegar a una representación suya concreta que tiene en cuenta solo sus componentes fundamentales: amplitud y fase.
Por lo tanto, podemos decir que:
A · cos (2π ft + φ )
equivale a:
A · e jφ
Esta última representación se puede denominar fasory, cuando se trata con las corrientes alternas, simplifica mucho los cálculos. Además, puedo pasar de una sinusoide de forma clásica a un fasor, y viceversa. Sin embargo, a la práctica, cuando se trabaja con fasores, no se tiene en cuenta la amplitud original de la onda sinusoidal, sino que se divide su valor por la raíz cuadrada de 2, porque así se trabaja con el valor efectivo de la sinusoide. El valor efectivo se puede definir para cada magnitud periódica y está relacionado con los valores medios. Si consideramos una sinusoide y la observamos durante un periodo de tiempo, esta tendrá una zona toda positiva y una, idéntica, negativa. Su valor medio es, por tanto, igual a 0, porque la onda es durante tanto tiempo positiva como negativa. Podría parecer que una onda sinusoidal no sea capaz de combinar nada si, al final, tiene un valor medio igual a 0.
Sabemos muy bien que esto no es así, puesto que, si no, en nuestras casas no tendríamos corriente alterna. Por esta razón se utiliza el valor eficaz o RMS (Root Mean Square) , que es igual al valor de la corriente continua que produciría la misma disipación de potencia (media) sobre una carga resistiva. Para calcular el valor eficaz de una onda sinusoidal, se necesita calcular el área de la sinusoide al cuadrado, dividida por su periodo, y todo ello bajo una raíz cuadrada. El cálculo proporciona un resultado muy sencillo y familiar para todos los electrónicos:
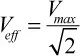
Operaciones sobre fasores
Hemos definido un fasor y hemos aprendido que corresponde a una representación cómoda para una sinusoide. Cuando utilizamos fasores, debemos basarnos en estas reglas.
Producto de un fasor por una constante
Una tensión sinusoidal s 1(t) corresponde a un fasor A 1. Si multiplico (o amplifico) la sinusoide s 1(t) por n veces, obtengo que también la amplitud del fasor se amplificará con la misma magnitud y será igual a:
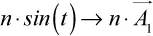
Si tengo dos magnitudes sinusoidales s 1y s 2, puedo sumarlas y obtener:
S 3( t ) = S 1( t ) + S 2( t )
La suma no cambia si utilizamos los fasores:
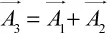
En las fórmulas electrónicas, a menudo hay que tener en cuenta la variación de la señal. Si tengo s 1( t ), me podría interesar conocer la rapidez con que cambia la señal en el tiempo, lo que equivale a saber la pendiente de la curva. En muchas fórmulas electrónicas, es necesario calcular este tipo de variaciones. Por ejemplo, al estudiar los condensadores observamos que la corriente que pasa por ellos es proporcional a la variación en el tiempo de la tensión en las placas. La variación de la tensión en el tiempo es comparable a la pendiente de la curva. Cuando queremos medir la pendiente de una calle, medimos cuánto sube y a lo largo de qué distancia. Con las dos medidas podemos determinar la pendiente, que, por último, se puede expresar como porcentaje. Cuando, mientras conducimos, nos encontramos con un cartel que indica que la pendiente de la carretera es del 10 %, significa que la carretera subirá como mínimo 10 m por cada 100 m que recorramos.
Читать дальше