Joseph J. Torres - Life in the Open Ocean

The first characteristic of fluids that must be appreciated for an understanding of viscosity is the “no‐slip condition” with respect to solids. That is, at the interface between a solid and a fluid flowing over it, the velocity of the fluid is zero. A zero‐velocity boundary layer is created, whose thickness depends on the velocity of the fluid flow. At the solid–fluid boundary, fluids stick to solids absolutely. Any object in a flow thus creates a shear, as the fluid particles at the no‐slip boundary must be moving at a different velocity than those at a distance from the body in the flow.

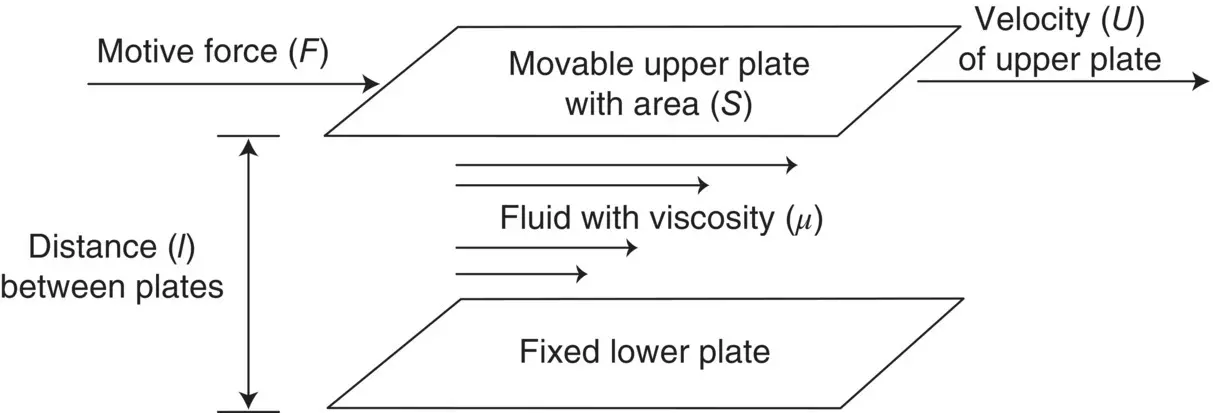
Figure 1.2 Dynamic viscosity ( μ ). A fluid’s “stickiness” or resistance to shear. Expressed mathematically as μ = Fl / US .

The resistance to shear is the dynamic viscosity of the fluid, and it is best described using the classical “flat plate” analogy. Imagine two plates of negligible thickness oriented parallel to one another and with a fluid between them ( Figure 1.2). The bottom plate is stationary, and the movable plate is pushed forward with a force that results in a constant velocity. Since the fluid at the boundary of each plate has zero velocity due to the no‐slip rule, the fluid between them is deformed or sheared, and a uniform velocity gradient develops between them in response to the constant pushing. The force needed to maintain the constant velocity depends upon the velocity itself, upon the area of the plate because the amount of fluid that needs to be moved is a function of the size of plate, and upon the viscosity of the fluid, or how easily the fluid is deformed. The resulting equation is:

(1.1)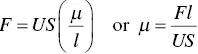

where U is velocity, S is the area of the plate, μ is viscosity, and l is the distance between the plates. Think of the flat plates as the bottom and top card in a deck of playing cards. The fluid is all the cards between them, and the stickiness between the cards determines how easy it is to deform the deck. Viscosity is that stickiness. The viscosity (dynamic viscosity) is an important property of fluids because it determines how easy it is to move them and to move through them.

A second type of viscosity is quite important in understanding flow around and through objects: the kinematic viscosity or υ. It is the ratio of dynamic viscosity ( μ ) to density ( ρ ):

(1.2)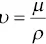

Kinematic viscosity is considerably less easy to grasp on an intuitive level, but it relates two important properties of a fluid that will be significant to us in examining the locomotion of open‐ocean fauna. Viscosity and density have much to do with patterns of flow around an organism. On the one hand, viscosity measures how adjacent particles retard a fellow fluid particle’s movement when it encounters a body in a flow. On the other, density is a measure of how likely it is that a fluid particle will keep moving. The ratio of the two forces, inertial and viscous, is the subject of our next topic, the Reynolds number.

Osborne Reynolds observed that a dye stream introduced into a liquid flowing through a pipe would yield a nice linear (laminar) flow or a turbulent disturbed one depending upon three characteristics of the liquid and one of the pipe. The velocity of the flow, the density of the liquid, the viscosity of the liquid, and the diameter of the pipe determined whether the flow was laminar or turbulent. Manipulating any one of the four variables was equally effective in changing the characteristics of the flow. The relationship between those variables is described in the equation for Reynolds number:

(1.3)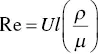

where U is the velocity of the flow, l is the diameter of the pipe, and ρ and μ are by now familiar as density and viscosity, respectively. You will also note that the ratio of density and viscosity gives us the inverse of the kinematic viscosity, which can then be put in the denominator:

(1.4)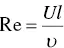

A Reynolds number of 2000 marks the transition between laminar and turbulent flow. The diameter of the pipe ( l ) for a swimming organism becomes instead the greatest length of the organism in the direction of flow.

The Reynolds number is a dimensionless number, i.e. it has no units, and it is a very useful tool for describing the characteristics of flow around a submerged body. It is the ratio of the inertial (velocity × characteristic length × density) to the viscous (dynamic viscosity) forces mentioned earlier. In fact, the Reynolds number can be derived by dividing the formula for momentum ( ρSU 2) (inertial force) by that for viscous force ( Eq. 1.1).

(1.5)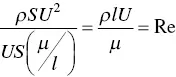

The derivation is done in slightly different ways in Vogel (1981) and in Denny (1993). I have followed Vogel’s derivation here. Both books are highly recommended for a more thorough treatment of the forces summarized here.

The useful property of Reynolds number is that you can get a good idea of the physical characteristics of a flow regime with a single number. Low Re (less than 1), such as that experienced by a protist or the moving limb of a swimming crustacean, is dominated by viscous forces. Flow will be laminar. A small swimming crustacean may have Re in the neighborhood of 100–2000 where inertial forces predominate (Torres 1984) but flow is largely laminar. In contrast, a tuna swimming at 10 m s −1with an Re of 30 000 000 (Vogel 1981) is in a highly turbulent flow regime. Most of the species of interest in this book live with Reynolds numbers in the 100s–1000s when moving and feeding.

To get an intuitive sense for the world in which pelagic species live, we need to know what forces they must generate or overcome in order to move and to breathe. Our next topic deals with two of the most important forces acting on any swimming animal: friction drag and pressure drag.

Recalling the no‐slip rule for a solid body in a flow, it follows logically that a swimming individual will be creating a shear as it moves its “no‐slip” form through the water. The shear will be resisted by the viscosity of the fluid just as in our example with the flat plate, and the magnitude of that resistance will depend on how much surface is exposed to the flow. The resistance is called the friction drag, or skin friction drag, and since friction is something we have all experienced, it is a pretty easy one to comprehend. Friction drag, being in the province of viscosity, is most important at low Reynolds numbers.

Pressure drag may be less easy to appreciate, but it is very important. If you envision a solid object in a flow ( Figure 1.3), e.g. a cylinder with its axis normal to the flow, it is an easy matter to see that the pressure on the object will be highest on its upstream face since it is oriented directly into the flow and takes the brunt of the moving fluid. The shape of the pipe results in an acceleration of the fluid as it passes over and under the pipe. Because of Bernoulli’s principle, the increased velocity of the fluid results in a decreased pressure on the downstream side of the cylinder. The differences in pressure from the upstream to the downstream side are rather like pushing from the front and sucking from the rear, and those differences create pressure drag. The expression for dynamic pressure ( q ) is: