Nirmal K. Sinha - Engineering Physics of High-Temperature Materials

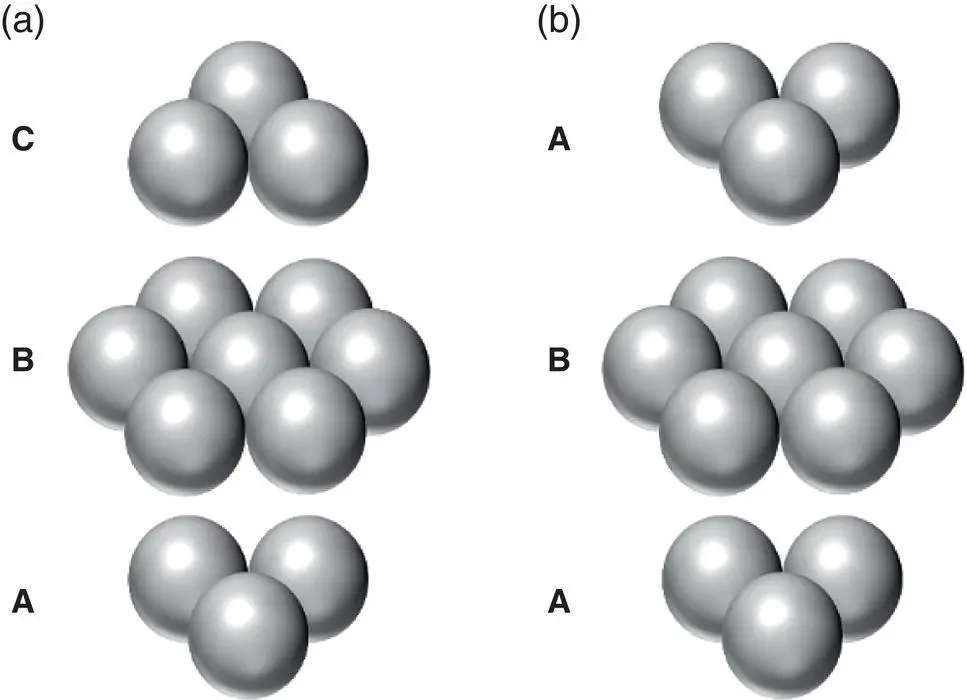
Figure 2.2 Stacking sequence in (a) FCC and (b) HCP crystals.

Variations of the three basic crystal structures – BCC, FCC, and HCP – give rise to a wide range of crystal structures. In addition, many solids have the ability to exist in more than one crystal structure. This is called polymorphism. Polymorphism often results due to exposure to different temperatures and pressures. For example, many metals will exist in a close‐packed structure (e.g. HCP) at low temperature, but will transform into the less dense BCC structure at higher temperatures.

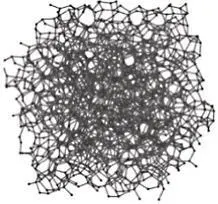
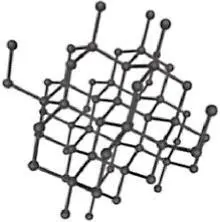
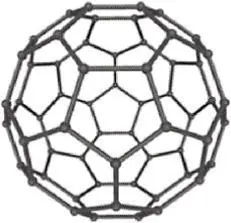
Allotropy is a special subset of polymorphism. Allotropes are specifically polymorphs of the elements. Elemental carbon is one of the most common examples of allotropy due to the range of structures it can take. Allotropes of carbon include amorphous coal, graphite (hexagonal crystal system), diamond (FCC variation) and nanocarbon structures (such as buckminsterfullerenes and nanotubes). Comparing the properties of some common carbon allotropes demonstrates the great impact that crystal structure and overall microstructure can have on the properties of materials ( Table 2.1).

Amorphous solids can best be described by what they are not. They are materials that exhibit elastic response like crystalline solids, but possess no crystal‐like long‐range order in the spatial arrangements of their atoms. Amorphous materials could be inorganic or organic and are also known as glasses and vitreous solids. Glasses are increasingly being used in wide‐ranging branches of science and technology. Bulk amorphous metals (aka metallic glasses) are increasingly being used as engineering materials owing to their extraordinary isotropic properties, including high strength, corrosion resistance, formability, and even biocompatibility (Khan et al. 2017; Jafary‐Zadeh et al. 2018). Molten minerals quenched to an amorphous state are used as analogs for magma (molten rocks) deep inside the surface of Earth (Davidovits 2005).

Table 2.1 Comparison of the properties of some basic carbon allotropes.

	Coal	Graphite	Diamond	Buckminsterfullerene (C60)	Carbon nanotubes
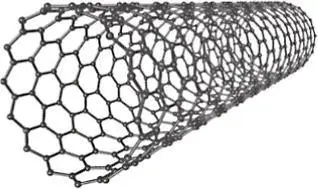Structure/hybridization	Amorphous (varies)	Trigonal planar (sp2)	Tetrahedral (sp3)	Spherical (sp2 and Sp3)	Between sp2 and sp3
Appearance	Dark black/gray, nonmetallic luster	Dark gray, metallic luster	Colorless (pure)	Black	Black
Hardness	Low	Medium	Very high	High	Very high
Tensile strength	Low	Medium	—	Medium	Very high
Thermal conductivity	Low	Low	High	High	High
Electrical conductivity	Varies	High	Insulator	Low	Semiconducting – metallic

RANDOM NETWORK

RANDOM COIL

RANDOM CLOSE‐PACKING

The atomic structure of glasses can be very complex. Three overarching structural models have arisen to describe most ideal amorphous materials.

1 The continuous random‐network model: This model describes a three‐dimensional network where an irregular network is formed through bridging atoms, but the bonding pattern at network sites is repeated. It is most applicable to covalently bonded glasses, such as oxide‐based glasses (Zachariasen 1932). In oxide‐based glasses, the oxygen atoms form bridges and network formers, such as silicon, phosphorus, or germanium, form strong bonds with them in a randomly arranged network structure. In addition, network modifiers, such as sodium and calcium, generally sit in ionic form within interstitial holes and can drastically alter the properties of the bulk material. The continuous random‐network model describes an ideal – fully amorphous – glass. In Section 2.4, we explore the structure of real glasses in more detail.

2 The random‐coil model: This model describes the disorder created by entangled chains through the use of three‐dimensional random walks (Flory 1949). In fact, the model presents a statistical distribution of conformations taken by all the chains in a population of macromolecules and is further complicated by chain length distributions, branching, and constrained rotation in real material. It is most applicable to glassy polymers, such as polystyrene and many plastics.

3 The random close‐packing model: This model describes an irregular structure of molecules that does not contain any short‐ or long‐range order or holes large enough to admit another molecule. It is based upon crystallographic models for liquid structure (Bernal 1959) and is most applicable to metallic glasses.

An exhaustive review of the knowledge gained on the structure of inorganic oxide and nonoxide glasses and the liquids they are derived from was carried out by Greaves and Sen (2007). They looked at the atomic structure, ranging from the local environments of individual atoms to the long‐range order, which can cover many interatomic distances. In this book, we will concentrate only on inorganic amorphous materials and, in particular, on silicate glass that is used extensively in domestic and industrial buildings, automobiles, and for household purposes. Even though silica‐based glasses have satisfied demands for a remarkable range of consumer goods for a long time throughout human history, the mechanism of glass cracking has not been well understood and is keeping glass scientists active (Michalske and Bunker 1987).

Most inorganic solids, like minerals, rocks, and ice, on Earth's surface are solidified or frozen from a liquid phase. The temperature at which a material transitions between the solid and liquid phases is denoted as the melting point ( T m) of the material. This transformation temperature represents the point where the free energy of the solid phase and that of the liquid phase are equal. Unless otherwise noted, this T mis assumed to be at standard pressure. However, there are several environmental aspects involved in the solidification process from liquid to solid. These are all contributing factors that determine the microstructure of the solid.

At a high level, during the solidification process, atoms/molecules from the fluid begin to bond together to form a nucleus. Homogeneous nucleation involves the clustering of liquid molecules/atoms to form a critical‐sized nucleus without an external interface. If a seed crystal of a desired structure is exposed to the melt, it can act as a nucleus and support in controlling the final structure. The nucleation process can also be triggered by the surface of an impurity (or structural material) that lowers the critical free energy required to form a stable nucleus. This process is called heterogeneous nucleation and, in practice, can control the solidification process.