Nirmal K. Sinha - Engineering Physics of High-Temperature Materials

On the other hand, under such basic classification schemes, “solids” are materials in which the particles are regularly spaced and form repeating structures in three dimensions; that is, they are crystalline in nature. Solids generally retain a fixed volume and shape and do not flow easily.

The outcome of such classification leads to some interesting areas to consider. For example, amorphous materials, such as traditional glasses, which are usually considered solid materials in everyday use, are classified as supercooled liquids (albeit this is debatable), and materials like liquid crystals, amorphous metals, and supercritical gases fall somewhat between the phase definitions. In addition, a fourth state, i.e. “plasma,” is introduced to describe matter at very high temperatures and pressures where the atoms start to break down resulting in a mixture of neutral atoms, free electrons, and charged ions. The sun, lightning, and beautifully colored auroras are examples of plasmas in nature.

Significant progress has been made in understanding the states and their boundaries, particularly for metals, metallic alloys, and ceramics (Reed‐Hill and Abbaschian 1992; chapter 10). The fluid states (liquid, gas, and plasma), though particularly important for process industries and for specific applications, are often not discussed when dealing with the compositions, physical metallurgy, and engineering mechanics revolving around microstructure–property relationships. Understanding the solid state is, however, of the utmost practical importance for all engineering applications for metals, alloys, and ceramics.

Due to the complex nature of materials, the modern‐day classification of states often relies on a more sophisticated system that focuses on the elastic response of the material. At a high level, in this scheme, solids respond to shear stress by the momentary relative motion of adjacent layers of particles whereas fluids undergo continuous relative motion or flow (DeVoe n.d.; chapter 2). This difference between states depends not only on temperature and pressure, but also on the timescale of observation. Time dependency will be a critical aspect explored throughout this text.

As materials, solids can largely be grouped into crystalline and amorphous materials. Crystalline solids are those in which the atoms are regularly spaced and form repeating structures in three dimensions. This definition of solids applies to the traditional classification of phases. Amorphous materials do not have any long‐range order in their structures, but they have demonstrated unique properties of interest to engineers.

The three‐dimensional structure or arrangement of atoms is called the crystal structure of the solid. The unit cells are the repeating structures in the crystal, and the smallest repeating unit is called the primitive unit cell. The Bravais lattice concept is generally used to define the structure. There are 14 Bravais lattices that define arrangements that can fill three‐dimensional space. Lattice constants refer to the physical dimensions of the unit cells and are generally denoted by a , b , and c .

To describe crystallography, points, direction, and planes are given indices that are used in conjunction with the lattice constants. Points are given labels, like points in a Cartesian coordinate system so that the point represented by coordinate ua , vb, and wc is u , v, and w units along the corresponding lattice direction. A direction is denoted with square brackets such that [ uvw ] represents a direction parallel to the direction of the origin with the point at coordinates ua , vb , and wc . A family of directions represents all directions in the lattice that are similar by symmetry and are denoted as < uvw >. In crystallography, planes are defined by their Miller indices. Miller indices rely on the reciprocal lattice vectors rather than the direct Bravais lattice. For simplicity, a plane with Miller index ( hkl ) represents the plane that passes through the points ( a/h , 0, 0), (0, b/k , 0), and (0, 0, c/l ). A family of planes represents all planes in the lattice that are similar by symmetry and are denoted as { hkl }. For more information on crystallography, there are several resources available, such as Vainshtein et al. (1982) and Mak and Gong‐Du (1992).

BODY‐CENTERED CUBIC

FACE‐CENTERED CUBIC

HEXAGONAL CLOSE‐PACKED

Nature's efficiency in packing leads to the abundance of three main crystal structures. While these structures do not describe all materials, their prevalence makes them important to dive into and enables understanding of similar structures. Two of these structures are based on a simple cubic arrangement. The simple cubic structure consists of atoms placed on each corner of a cube. The simple cubic unit cell is thus a cube containing 1/8 of each corner atom for a total of one atom per unit cell. The distance between the corners of the cube is called the unit cell dimension, which is commonly denoted as the lattice constant, “ a .” Assuming the highest packing efficiency in the simple cube and the model of an atom as incompressible spheres of radius “ r ” we have a = 2 r . Three of the most common crystal structures in nature are the body‐centered cubic (BCC) structure, the face‐centered cubic (FCC) structure, and the hexagonal close‐packed (HCP) structure. As can be seen in Figure 2.1, the first two structures are based on the simple cube.

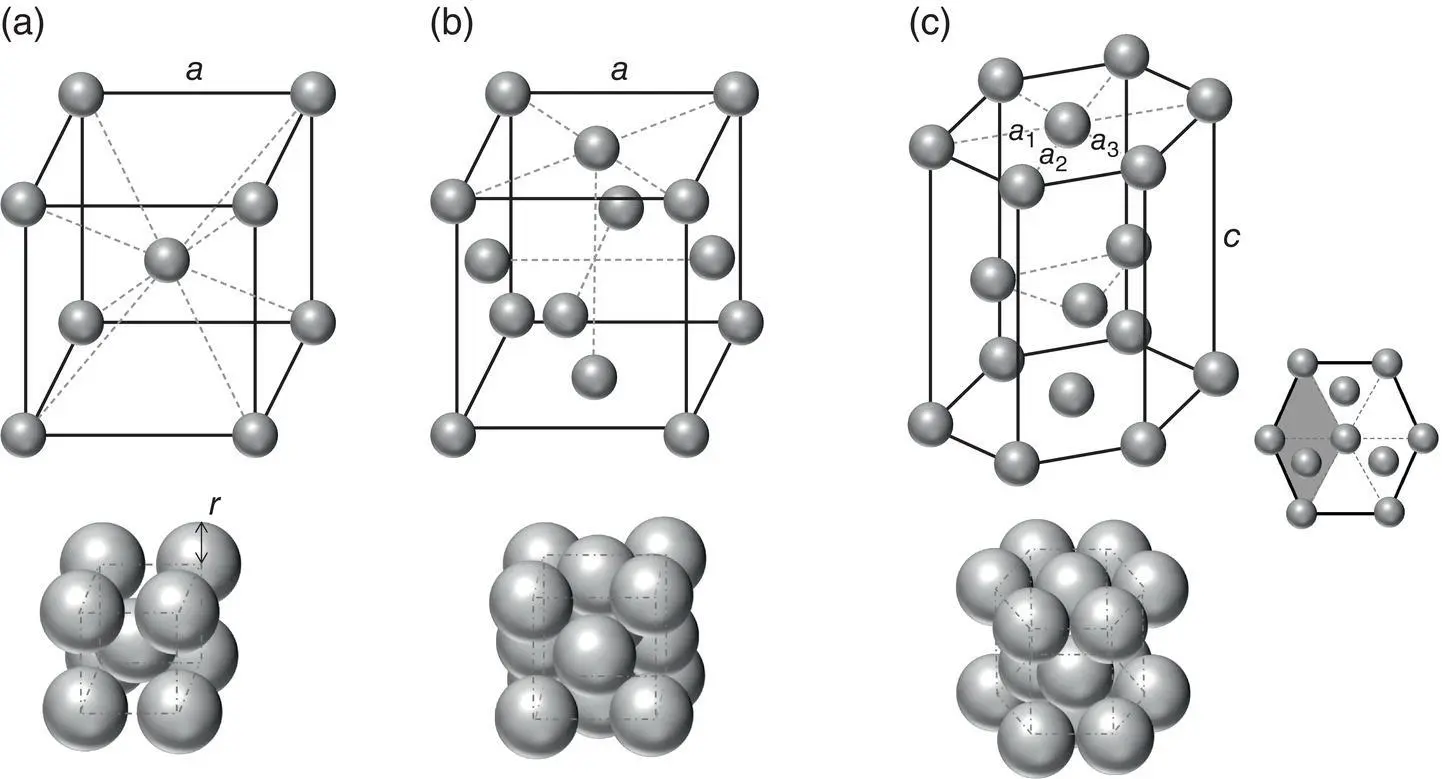
Figure 2.1 Basic crystal lattice structures: (a) BCC, (b) FCC, and (c) HCP crystals. The upper stick–ball representations demonstrate the basic atomic arrangement while the lower images represent the close packing. The side inset in (c) represents the top‐down view of the HCP structure with the shaded region demonstrating the primitive unit cell.

The BCC structure takes the simple unit cell and increases the packing efficiency by having an additional atom at the center of the cube. Thus, there are two atoms per unit cell. The diagonal passing through the center of the BCC unit cell is called the close‐packed direction because atoms along the diagonal touch each other. The length of the diagonal is thus equal to 4 r and 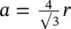. Common BCC materials include iron, chromium, and tungsten.

The FCC structure has an atom at each corner of the unit cell plus an atom at the center of each face of the unit cell. Thus, there are four atoms per unit cell. The closed‐packed directions of the FCC structure are the diagonals across each face of the unit cell, and this arrangement gives rise to the closest packing of spheres in a cube. When viewed from a 45° angle (i.e. viewing the (111) layers) and taking a slightly larger view, relative to the unit cell, the FCC structure can be seen to be made up of three types of planes. It is thus said to have an ABC stacking sequence ( Figure 2.2). Common FCC materials include aluminum, gold, and nickel.

The HCP structure, which is the last of the most common structures, also gives rise to the same packing efficiency as does the FCC structure and thus the closest packing of spheres in a cube. As shown in Figure 2.2, it can be seen to have an ABA stacking sequence. The HCP unit cell is not based on a simple cube, but rather, as its name implies, on a hexagonal structure with atoms at each corner of the hexagon. An additional atom is located at the center of each face of the hexagon and three more atoms are located in a plane between the hexagonal faces. The hexagonal unit cell contains within it three primitive unit cells (the smallest repeating unit). This primitive cell is represented as the shaded region in the top‐down view of the HCP unit cell in Figure 2.1c. The larger hexagonal unit cell is easier to visualize, and it contains six atoms per cell. Common HCP metallic materials include magnesium, zinc, and titanium. Snow and ice, which are among the most abundant, but nonmetallic, materials on Earth's surface, also belong to the hexagonal family system, though these materials do not have the close‐packed structure at normal pressures and temperatures on earth’s surface. Ice is discussed in greater detail in Section 2.6.