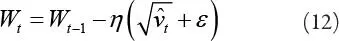Una vez calculado el nuevo estado C t de la capa LSTM, se puede obtener el valor de sus puertas de salida y, como consecuencia, la salida final h t de la capa LSTM.
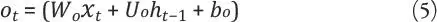
Donde o t es el valor de la puerta de salida de la red LSTM y σ es la función de activación.

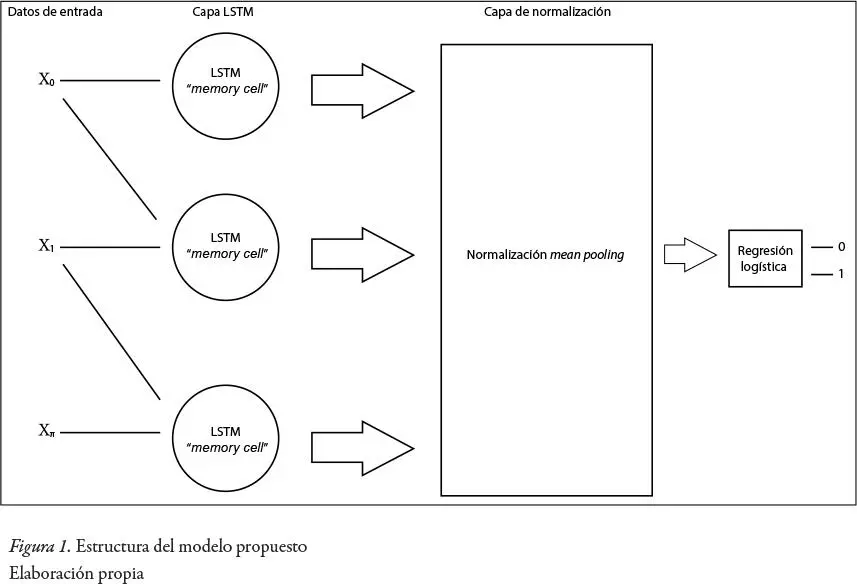
La estructura final del modelo a usar consiste en una sola capa de redes neuronales LSTM, luego se implementará una capa de normalización ( mean pooling ), esto va a disminuir la variancia entre los valores, debido a que se va a tomar un promedio de la cantidad de datos para realizar un mapeo final de features . Después se implementará una capa de regresión logística para obtener una mayor eficacia a la hora de clasificar las noticias.
2.3 Algoritmo de optimización
Para incrementar la eficiencia de la red neuronal propuesta, se ha decidido implementar un algoritmo llamado Adam, el cual sirve para escoger el mejor learning rate para que el entrenamiento de la red neuronal sea el más rápido y efectivo posible (Kingma et al ., 2014).
Adam es un algoritmo de learning rate adaptativo, lo que significa que calcula learning rates individuales para diferentes parámetros. Su nombre se deriva de la estimación del momento adaptativo, y la razón por la que se llama así es porque Adam usa estimaciones del primer y segundo momento del gradiente para adaptar la velocidad de aprendizaje para cada weight de la red neuronal.
Adam utiliza los gradientes elevados al cuadrado para escalar la velocidad de aprendizaje como el algoritmo RMSprop (Tieleman y Hinton, 2012) y aprovecha el impulso al usar la media móvil de los gradientes en lugar de solo la gradiente como el algoritmo stochastic gradient descent .
Para estimar los momentos, Adam utiliza promedios móviles exponenciales, calculados en el gradiente evaluado en un minilote actual:

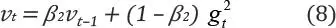
Donde m t y v t son los promedios móviles, g es la gradiente del minilote actual y los β son los hiperparámetros del algoritmo. Ambos tienen un valor default de 0,9 y 0,999, respectivamente
La fórmula para obtener el promedio móvil m t también puede ser representada por la siguiente ecuación:
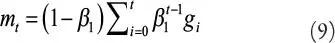
Después de esto se necesita realizar un paso llamado “ bias correction ”, esto quiere decir que se necesita corregir el valor inicial de m t y v t , para ello se realizan las siguientes transformaciones:


Para finalizar, se utilizan estos promedios móviles 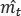 y
y 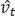 para escalar la learning rate individualmente para cada parámetro. La forma en que se hace en Adam es simple, para realizar una actualización de weights hacemos lo siguiente:
para escalar la learning rate individualmente para cada parámetro. La forma en que se hace en Adam es simple, para realizar una actualización de weights hacemos lo siguiente:
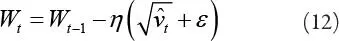
Donde W t es una matriz weights y la η es el tamaño del step (Zhang, Ma, Li y Wu, 2017).
2.4 Impacto de las noticias positivas
Para poder validar la hipótesis se decidió usar el test PANAS (Positive and Negative Affect Schedule).
Fue desarrollado en 1988 por Watson, Clark y Tellegen con el objetivo de medir de una forma más pura el efecto negativo o positivo de algún evento en específico (Watson, Clark y Tellegen, 1988). En un inicio el test PANAS contaba con 60 ítems (sentimientos) para determinar el sentimiento negativo o positivo, pero luego se realizó una reducción de la lista, basada en el coeficiente de importancia, y al final se obtuvieron 20 ítems, 10 para el sentimiento negativo y 10 para el sentimiento positivo (Watson, Clark y Tellegen, 1988).
Los resultados de este cuestionario fueron alentadores, porque fueron acertados, presentando los siguientes porcentajes: para la escala de sentimiento positivo, el coeficiente alfa de Cronbach (Cronbach, 1951) fue de 0,86 a 0,90; para la escala de sentimiento negativo, 0,84 a 0,87 (Watson, Clark y Tellegen, 1988).
3. RESULTADOS
3.1 Validación del modelo LSTM
Luego de haber implementado el modelo, se probó su eficacia utilizando el método de validación cruzada k-folds con un k=10 (Kohavi, 1995). Los resultados fueron los siguientes:
Tabla 2
Resultados de la validación cruzada k-folds
| Validación cruzada k-folds (k=10) |
| Folds (k) |
Accuracy |
| 1 |
86,56 % |
| 2 |
85,36 % |
| 3 |
86,85 % |
| 4 |
89,37 % |
| 5 |
88,29 % |
| 6 |
85,67 % |
| 7 |
89,95 % |
| 8 |
91,51 % |
| 9 |
88,30 % |
| 10 |
87,92 % |
|
Promedio: 87,98 % |
Elaboración propia
Para comparar la efectividad del modelo se implementaron otros dos métodos que también son usados en la actualidad:
1) Naive Bayes
2) Red neuronal recurrente (RNN)
El método usado para la validación, por consistencia, fue el de validación cruzada k-folds (k=10).
Tabla 3
Resultados de la validación cruzada k-folds
| Validación cruzada k-folds (k=10) |
| Folds (k) |
Accuracy |
| 1 |
79,89 % |
| 2 |
83,25 % |
| 3 |
79,28 % |
| 4 |
81,59 % |
| 5 |
83,17 % |
| 6 |
79,03 % |
| 7 |
79,98 % |
| 8 |
80,55 % |
| 9 |
81,71 % |
| 10 |
82,99 % |
|
Promedio: 81,14 % |
Elaboración propia
2) Red neuronal recurrente RNN
Читать дальше

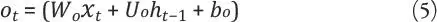



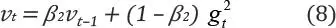
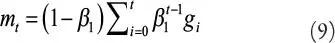


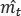 y
y 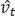 para escalar la learning rate individualmente para cada parámetro. La forma en que se hace en Adam es simple, para realizar una actualización de weights hacemos lo siguiente:
para escalar la learning rate individualmente para cada parámetro. La forma en que se hace en Adam es simple, para realizar una actualización de weights hacemos lo siguiente: