Computational Statistics in Data Science

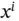The directed edges in the network represent weights from a node in one layer to another node in the next layer. We denote the weight from a node in the input layer to a node 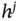in the hidden layer as 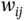. The weight from a node 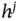in the hidden layer to a node 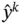in the output layer will be denoted 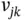. In each of the input and hidden layers, we introduce intercept nodes , denote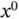d and 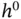, respectively. Weights from them to any other node are called biases . Each node in a given layer is connected by a weight to every node in the layer above except the intercept node.

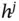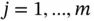The value of each node in the hidden and output layers is determined as a nonlinear transformation of the linear combination of the values of the nodes in the previous layers and the weights from each of those nodes to the node of interest. That is, the value of , , is given by 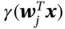, where 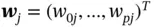, , 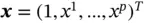and 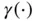is a nonlinear transformation with range in the interval 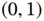. Similarly, the value of 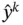, , 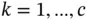is given by 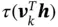, where 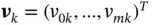, , 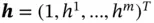and 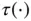is also a nonlinear transformation with a range in the interval .

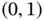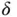More formally, the map provided by an MLP from a sample 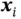to 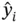can be written as follows: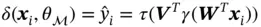

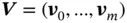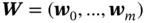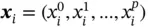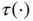where , , , and and 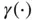are nonlinear functions.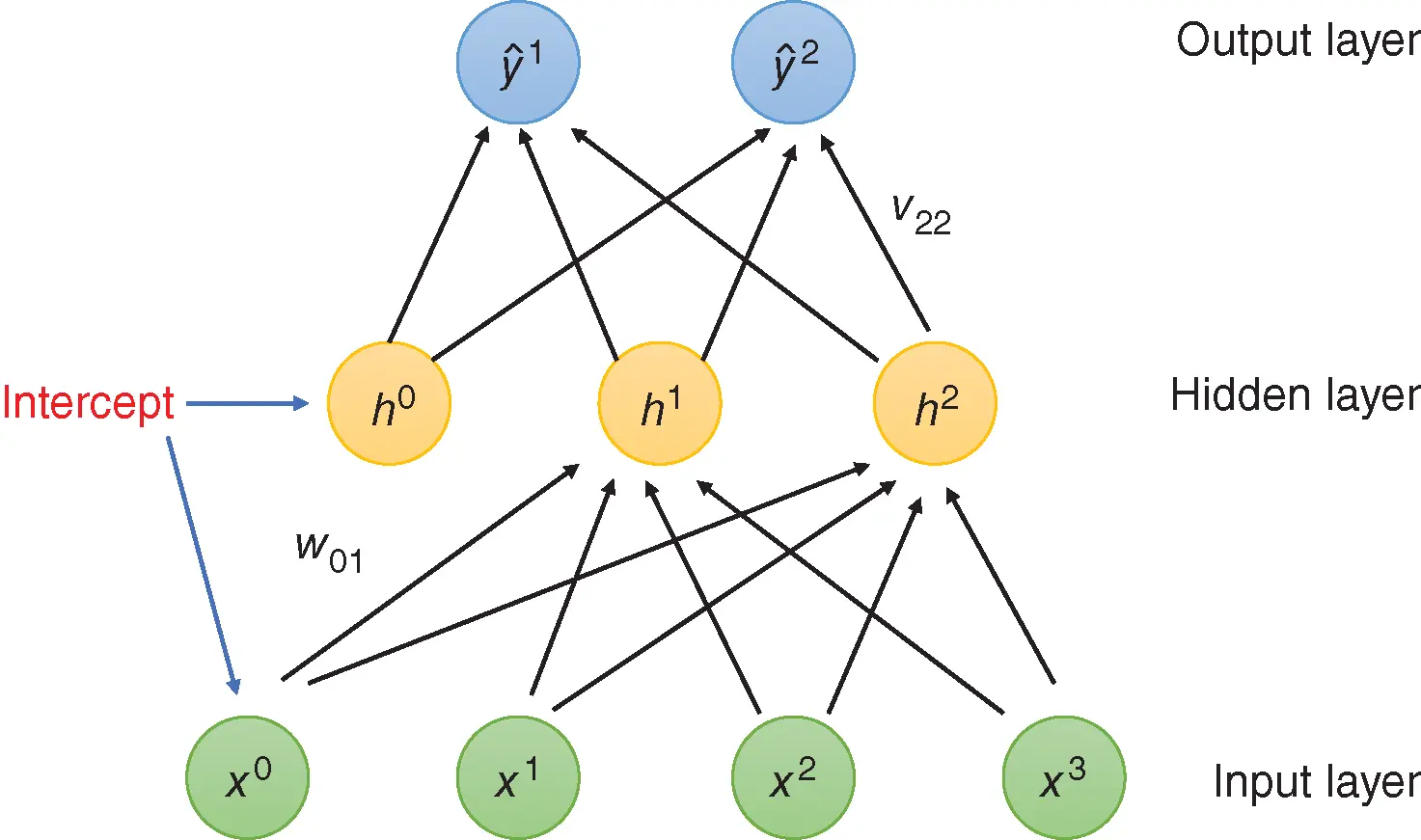

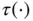Figure 1 An MLP with three layers.

Most often, and 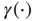are chosen to be the logistic function 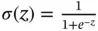. This function is often chosen for the following desirable properties: (i) it is highly nonlinear, (ii) it is monotonically increasing, (iii) it is asymptotically bounded at some finite value in both the negative and positive directions, and (iv) its output lies in the interval 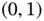, so that it stays relatively close to 0. However, Yann LeCun recommends that a different function be used: 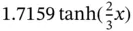. This function retains all of the desirable properties of the logistic function and has the additional advantage of being symmetric about the origin, which results in outputs closer to 0 than the logistic function.