Machine learning methods are grouped into two main categories, based on what they aim to achieve. The first category is known as supervised learning . In supervised learning, each observation in a dataset comes attached with a label . The label, similar to a response variable, may represent a particular class the observation belongs to (categorical response) or an output value (real‐valued response). In either case, the ultimate goal is to make inferences on possibly unlabeled observations outside of the given dataset. Prediction and classification are both problems that fall into the supervised learning category. The second category is known as unsupervised learning . In unsupervised learning, the data come without labels, and the goal is to find a pattern within the data at hand. Unsupervised learning encompasses the problems of clustering, density estimation, and dimension reduction.
Here, we state the problem of supervised learning explicitly. We have a set of training data 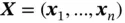 , where
, where 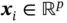 for all
for all 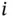 , and a corresponding set of labels
, and a corresponding set of labels 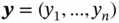 , which can represent either a category membership or a real‐valued response. We aim to construct a function
, which can represent either a category membership or a real‐valued response. We aim to construct a function 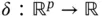 that maps each input
that maps each input 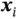 to a predicted label
to a predicted label 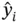 . A given supervised learning method
. A given supervised learning method 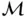 chooses a particular form
chooses a particular form 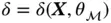 , where
, where 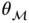 is a vector of parameters based on
is a vector of parameters based on 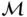 .
.
We wish to choose 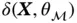 to minimize an error function
to minimize an error function 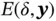 . The error function is most commonly taken to be the sum of square errors in which case the goal is to choose an optimal
. The error function is most commonly taken to be the sum of square errors in which case the goal is to choose an optimal 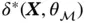 such that
such that
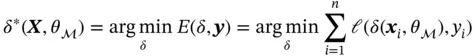
where 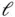 can be any loss function that evaluates the distance between
can be any loss function that evaluates the distance between 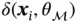 and
and 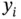 , such as cross‐entropy loss and square loss.
, such as cross‐entropy loss and square loss.
The form of the function 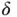 will usually be fairly complex, so attempting to find
will usually be fairly complex, so attempting to find  via direct differentiation will not be feasible. Instead, we use gradient descent to minimize the error function.
via direct differentiation will not be feasible. Instead, we use gradient descent to minimize the error function.
Gradient descent is a general optimization algorithm that can be used to find the minimizer of any given function. We pick an arbitrary starting point, and then at each time point, we take a small step in the direction of the greatest decrease, which is given by the gradient. The idea is that if we repeatedly do this, we will eventually arrive at a minimum. The algorithm guarantees a local minimum, but not necessarily a global one [4]; see Algorithm 1.
Gradient descent is often very slow in machine learning applications, as finding the true gradient of the error criterion usually involves iterating through the entire dataset. Since we need to calculate the gradient at each time step of the algorithm, this leads to having to iterate through the entire dataset a very large number of times. To speed up the process, we instead use a variation on gradient descent known as stochastic gradient descent . Stochastic gradient descent involves approximating the gradient at each time step with the gradient at a single observation, which significantly speeds up the process [5]; see Algorithm 2.


3 Feedforward Neural Networks
3.1 Introduction
A feedforward neural network, also known as a multilayer perceptron (MLP), is a popular supervised learning method that provides a parameterized form for the nonlinear map 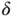 from an input to a predicted label [6]. The form of
from an input to a predicted label [6]. The form of 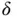 here can be depicted graphically as a directed layered network, where the directed edges go upward from nodes in one layer to nodes in the next layer. The neural network has been seen to be a very powerful model, as they are able to approximate any Borel measurable function to an arbitrary degree, provided that parameters are chosen correctly.
here can be depicted graphically as a directed layered network, where the directed edges go upward from nodes in one layer to nodes in the next layer. The neural network has been seen to be a very powerful model, as they are able to approximate any Borel measurable function to an arbitrary degree, provided that parameters are chosen correctly.
We start by describing a simple MLP with three layers, as depicted in Figure 1.
The bottom layer of a three‐layer MLP is called the input layer , with each node representing the respective elements of an input vector. The top layer is known as the output layer and represents the final output of the model, a predicted vector. Again, each node in the output layer represents the respective predicted score of different classes. The middle layer is called the hidden layer and captures the unobserved latent features of the input. This is the only layer where the number of nodes is determined by the user of the model, rather than the problem itself.
Читать дальше

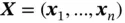 , where
, where 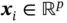 for all
for all 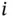 , and a corresponding set of labels
, and a corresponding set of labels 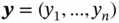 , which can represent either a category membership or a real‐valued response. We aim to construct a function
, which can represent either a category membership or a real‐valued response. We aim to construct a function 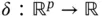 that maps each input
that maps each input 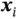 to a predicted label
to a predicted label 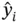 . A given supervised learning method
. A given supervised learning method 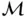 chooses a particular form
chooses a particular form 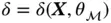 , where
, where 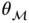 is a vector of parameters based on
is a vector of parameters based on 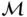 .
.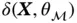 to minimize an error function
to minimize an error function 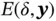 . The error function is most commonly taken to be the sum of square errors in which case the goal is to choose an optimal
. The error function is most commonly taken to be the sum of square errors in which case the goal is to choose an optimal 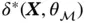 such that
such that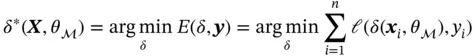
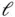 can be any loss function that evaluates the distance between
can be any loss function that evaluates the distance between 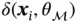 and
and 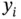 , such as cross‐entropy loss and square loss.
, such as cross‐entropy loss and square loss.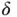 will usually be fairly complex, so attempting to find
will usually be fairly complex, so attempting to find  via direct differentiation will not be feasible. Instead, we use gradient descent to minimize the error function.
via direct differentiation will not be feasible. Instead, we use gradient descent to minimize the error function.

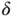 from an input to a predicted label [6]. The form of
from an input to a predicted label [6]. The form of  here can be depicted graphically as a directed layered network, where the directed edges go upward from nodes in one layer to nodes in the next layer. The neural network has been seen to be a very powerful model, as they are able to approximate any Borel measurable function to an arbitrary degree, provided that parameters are chosen correctly.
here can be depicted graphically as a directed layered network, where the directed edges go upward from nodes in one layer to nodes in the next layer. The neural network has been seen to be a very powerful model, as they are able to approximate any Borel measurable function to an arbitrary degree, provided that parameters are chosen correctly.![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)










