Der Strom durch eine Fläche A berechnet sich als Flächenintegral der Stromdichte.
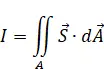 |
( 2 - 1 ) |
Ist die Stromdichte ungleichmäßig über einen Leiterquerschnitt verteilt (z.B. durch den Skineffekt), dann kann u.U., je nach analytischer Beschreibung der Verteilung, das Integral gelöst werden.
Verallgemeinerte Problemstellungen zu symmetrischen Basisanordnungen (Kugelsymmetrie, Zylindersymmetrie) sind oft so angelegt, dass bei entsprechender Bezugsfläche (Kugeloberfläche, Zylindermantel) der Betrag der Stromdichte über dieser Fläche konstant ist. In diesen Fällen vereinfacht sich das Stromdichteintegral wieder zu einer einfachen Multiplikation
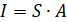 |
( 2 - 2 ) |
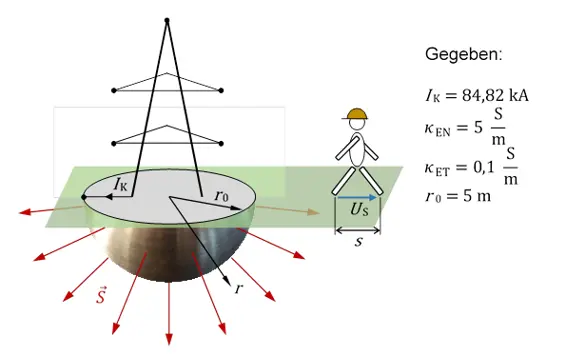
Ein Hochspannungsmast ist mit einem ideal leitfähigen, halbkugelförmigen Erder versehen. Durch einen Defekt kommt es zu einem Kurzschluss, bei dem der Kurzschlussstrom I Kins Erdreich abfließt. Das Strömungsfeld bildet sich dabei ausschließlich in radialer Richtung im Erdreich aus.
a) Wie groß sind Stromdichte 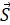 und elektrische Feldstärke
und elektrische Feldstärke 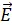 im Erdreich?
im Erdreich?
b) Wie groß ist für die Fälle:
1. Nasse Erde: 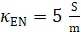
2. Trockene Erde: 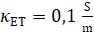
die Schrittspannung U S, wenn ein Unglücklicher mit einem Fuß direkt auf der Kante des Erders bei r = r 0steht und die Schrittweite s = 1 m beträgt, so dass der zweite Fuß bei r = r 0+ 1 m aufsetzt?
Lösung:
a) Wählt man als Integrationsfläche für die Stromdichte eine Halbkugelfläche mit dem Radius r , so hat die Stromdichte an jedem Ort den gleichen Betrag und ist immer parallel zum Flächennormalenvektor.
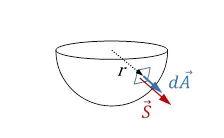
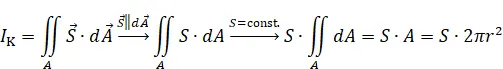
Das Skalarprodukt wird zu einem Produkt von Skalaren, die für gleiches r konstante Stromdichte kann vor das Integral geschrieben werden und das Integral über die Halbkugelfläche ergibt den bekannten Ausdruck für die halbe Kugeloberfläche.
Stellt man die Gleichung nach der gesuchten Stromdichte um, ergibt sich
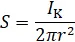
Für die Feldstärke folgt
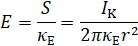
b) Die Spannung wird aus dem Wegintegral der Feldstärke berechnet. Der Integrationsweg in radialer Richtung ist parallel zu 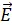 und somit wird auch hier das Skalarprodukt zu einem Produkt von Skalaren.
und somit wird auch hier das Skalarprodukt zu einem Produkt von Skalaren.
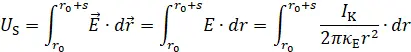
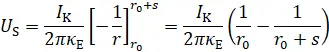
Einsetzen der Zahlenwerte:
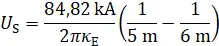
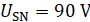
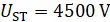
In einem Experiment soll in einem koaxialen, rohrförmigen Durchlauferhitzer Wasser durch direkten Stromdurchgang erwärmt werden.
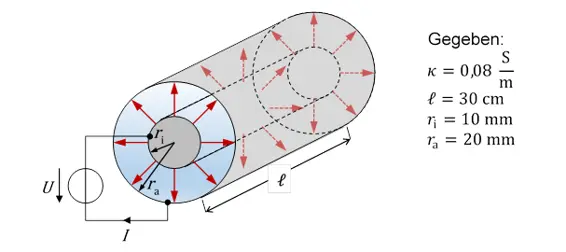
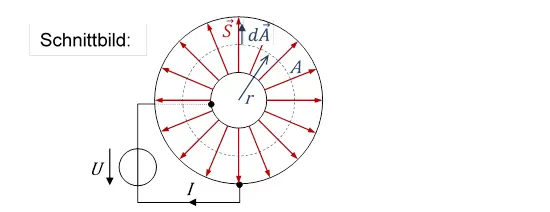
Berechnen Sie bei gegebenem Strom I die Stromdichte in Abhängigkeit vom Radius unter der Annahme, dass die Feldlinien exakt radial verlaufen.
2.3 Vorgehen bei Widerstandsberechnungen
Für die Berechnung des Widerstands einer Anordnung ist allgemein wie folgt vorzugehen:
· Den Strom I zunächst als gegeben annehmen.
· Die Stromdichte S mittels 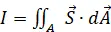 bzw.
bzw. 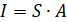 berechnen.
berechnen.
Der qualitative Feldverlauf muss bekannt sein.
· Die elektrische Feldstärke 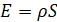 berechnen.
berechnen.
· Die Spannung 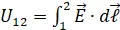 zwischen den Klemmen der Anordnung berechnen.
zwischen den Klemmen der Anordnung berechnen.
· Schließlich den angenommenen Strom I über 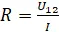 eliminieren.
eliminieren.
Einfache Anordnungen können gegebenenfalls auch auf Reihen- oder Parallelschaltungen von Widerständen zurückgeführt werden.
Berechnen Sie den Widerstand der Anordnung in Aufgabe 1.
Der gegebene Zylinderausschnitt wird von einen Strom I durchflossen. Die vordere und die hintere Fläche sind ideal leitfähige Kontakte.
Читать дальше

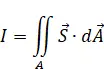
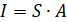

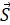 und elektrische Feldstärke
und elektrische Feldstärke 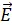 im Erdreich?
im Erdreich?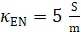
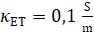

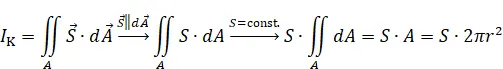
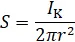
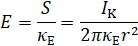
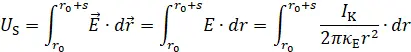
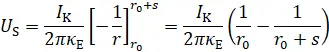
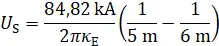
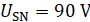
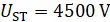


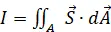 bzw.
bzw. 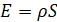 berechnen.
berechnen.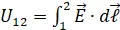 zwischen den Klemmen der Anordnung berechnen.
zwischen den Klemmen der Anordnung berechnen.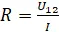 eliminieren.
eliminieren.










