Grundlagen der Elektrotechnik
Wechselstromtechnik
von
Prof. Dr.-Ing. Michael Koch
Prof. Dr.-Ing. Joachim Patzke
Version 3.1
Grundlagen der Elektrotechnik – Wechselstromtechnik
Michael Koch, Joachim Patzke
Copyright: © 2019 M. Koch;J. Patzke
Benutzungshinweise zum eBook
Aktuelle eBook-Formate sind für die Darstellung naturwissenschaftlicher Inhalte nicht optimal geeignet, da Sie auf einer Fließtextstruktur basieren. Bilder, Grafiken und Formeln werden in der Regel mit einer festen Größe dargestellt. Der Text ist hingegen skalierbar, sodass eine feste Zuordnung zwischen Text- und Bildgröße nicht erzwungen werden kann. Es bleibt daher dem Benutzer überlassen, beim Lesen eine sinnvolle Textgröße zu wählen, die in einer guten Relation zu Bildern und Formeln steht und darüber hinaus zu einer übersichtlichen Formatierung der enthaltenen Tabellen führt.
Inhalt
1 Grundbegriffe und Signalformen. 5 1 Grundbegriffe und Signalformen Signale lassen sich in Gleichgrößen und zeitabhängige (veränderliche) Größen unterteilen. Gleichgrößen ändern ihren Wert über der Zeit nicht (vgl. [ 1 ]). Der Verlauf einer zeitabhängigen Größe ist dagegen beliebig und oft schwer zu ermitteln bzw. zu beschreiben (Abbildung 1-1). Abbildung 1-1 Gleichgröße und zeitabhängige Größe Oft genügt es, die zeitabhängige Größe durch einige Kennwerte zu beschreiben, die ihre wichtigsten Eigenschaften enthalten.
1.1 Mittelwert 5 1.1 Mittelwert Eine wichtige Kenngröße ist der Mittelwert in einem Intervall . Abbildung 1-2 Mittelwert einer zeitabhängigen Größe Der Mittelwert schließt mit der Zeitachse die gleiche Fläche ein wie der Funktionsverlauf u ( t ) in diesem Intervall: Mittelwert ∙ Intervallbreite = Fläche unter der Kurve ( 1-1 ) Definition: ( 1-2 ) Der Mittelwert wird auch als arithmetischer Mittelwert, linearer Mittelwert oder Gleichwert bezeichnet. Ist der Mittelwert einer zeitabhängigen Größe Null, heißt diese Wechselgröße , andernfalls Mischgröße . ðJede Mischgröße kann durch Abziehen des Mittelwerts in eine Wechselgröße und eine Gleichgröße zerlegt werden Abbildung 1-3 Zerlegung in Gleich- und Wechselgröße
1.1.1 Aufgabe 1. 6 1.1.1 Aufgabe 1 Berechnen Sie den Mittelwert des dargestellten Signalverlaufs.
1.2 Gleichrichtwert 7 1.2 Gleichrichtwert Eine weitere wichtige Kenngröße in der Elektrotechnik ist der Gleichrichtwert. Hier wird der Mittelwert vom Betrag der zeitabhängigen Größe gebildet. ( 1-3 ) Die Betragsbildung bedeutet ein „Hochklappen“ aller negativen Funktionsteile vor der Integration. Abbildung 1-4 Gleichrichtung einer zeitabhängigen Größe Der Gleichrichtwert ist wichtig bei der Messung von Wechselgrößen. Schaltungstechnisch lässt sich die Betragsbildung z.B. mit einem Brückengleichrichter realisieren (Abbildung 1-5). Abbildung 1-5 Brückengleichrichter
1.2.1 Aufgabe 2. 8 1.2.1 Aufgabe 2 a) Zeichnen Sie den Verlauf von . b) Berechnen Sie den Gleichrichtwert.
1.3 Quadratischer Mittelwert 8
1.3.1 Aufgabe 3. 9
1.4 Periodische Größen. 10
1.4.1 Mittelwerte periodischer Größen. 11
1.4.2 Wichtige Kennzahlen periodischer Größen. 12
1.4.3 Aufgabe 4. 13
1.4.4 Aufgabe 5. 13
1.5 Harmonische Schwingungen. 14
1.5.1 Mittelwerte und Kennzahlen. 15
2 Wechselstromrechnung. 19
2.1 Bauelemente der Wechselstromtechnik. 19
2.2 Augenblickswerte und Kirchhoffsche Sätze. 20
2.3 Zeigerdarstellung. 21
2.3.1 Erstellung von Zeigerbildern. 23
2.3.2 Beispielaufgabe. 23
2.4 Komplexe Wechselstromrechnung. 25
2.5 Grundelemente in Wechselstromnetzwerken. 28
2.5.1 Impedanz und Admittanz. 28
2.5.2 Zusammenfassung. 30
2.5.3 Beispiel 1. 31
2.6 Operatorendiagramme. 31
2.7 Aufgaben. 32
2.7.1 Aufgabe 6. 32
2.7.2 Aufgabe 7. 32
2.7.3 Aufgabe 8. 32
2.8 Vorgehen bei der Berechnung von Wechselstromkreisen. 33
2.8.1 Beispiel 2. 33
2.9 Aufgaben. 35
2.9.1 Aufgabe 9. 35
2.9.2 Aufgabe 10. 35
2.9.3 Aufgabe 11. 36
2.9.4 Aufgabe 12. 36
2.9.5 Aufgabe 13. 37
2.9.6 Aufgabe 14. 37
2.9.7 Aufgabe 15. 38
2.9.8 Aufgabe 16. 39
2.9.9 Aufgabe 17. 39
2.9.10 Aufgabe 18. 39
2.9.11 Aufgabe 19. 40
2.9.12 Aufgabe 20. 40
3 Leistung im Wechselstromkreis. 41
3.1 Augenblicksleistung der Grundelemente. 43
Ohmscher Widerstand. 43
Induktivität 43
Kapazität 43
3.2 Wirk- und Blindleistung. 45
3.3 Komplexe Leistung. 47
3.3.1 Leistung in der Impedanz. 48
3.3.2 Vorzeichen der Blindleistung. 48
3.4 Aufgaben. 50
3.4.1 Aufgabe 21. 50
3.4.2 Aufgabe 22. 50
3.4.3 Aufgabe 23. 51
3.4.4 Aufgabe 24. 51
3.5 Leistungsanpassung. 52
3.5.1 Wirkleistungsanpassung. 52
3.5.2 Scheinleistungsanpassung. 54
3.5.3 Aufgabe 25. 55
4 Schwingkreise. 57
4.1 Reihenschwingkreis. 58
4.1.1 Strom und Spannungen. 59
4.1.2 Güte. 62
4.1.3 Zeigerdiagramm.. 62
4.1.4 Grenzfrequenzen und Bandbreite. 62
4.2 Parallelschwingkreis. 65
4.2.1 Strom und Spannungen. 66
4.2.2 Zeigerdiagramm.. 67
4.2.3 Grenzfrequenzen und Bandbreite. 67
4.3 Aufgaben. 69
4.3.1 Aufgabe 26. 69
4.3.2 Aufgabe 27. 69
5 Ortskurven. 71
5.1 Inversion von Ortskurven. 72
5.2 Ortskurven der Grundschaltungen. 74
5.2.1 Reihenschaltungen. 74
5.2.2 Parallelschaltungen. 75
5.3 Ortskurvenparameter 76
5.4 Aufgaben. 77
5.4.1 Aufgabe 28. 77
5.4.2 Aufgabe 29. 77
5.4.3 Aufgabe 30. 78
5.4.4 Aufgabe 31. 78
5.4.5 Aufgabe 32. 79
5.4.6 Aufgabe 33. 79
6 Drehstrom.. 80
6.1 Dreiphasengenerator 80
6.2 Verbraucherschaltungen. 82
6.2.1 Last in Sternschaltung mit angeschlossenem Sternpunkt 82
6.3 Aufgaben. 85
6.3.1 Aufgabe 34. 85
6.3.2 Aufgabe 35. 85
6.3.3 Aufgabe 36. 86
7 Anhang. 87
7.1 Verwendete Formelzeichen. 87
7.2 Abbildungsverzeichnis. 88
7.3 Tabellenverzeichnis. 90
7.4 Literaturverzeichnis. 91
7.4.1 Skriptum.. 91
7.4.2 Weiterführende Literatur 91
1 Grundbegriffe und Signalformen
Signale lassen sich in Gleichgrößen und zeitabhängige (veränderliche) Größen unterteilen. Gleichgrößen ändern ihren Wert über der Zeit nicht (vgl. [ 1 ]). Der Verlauf einer zeitabhängigen Größe ist dagegen beliebig und oft schwer zu ermitteln bzw. zu beschreiben (Abbildung 1-1).
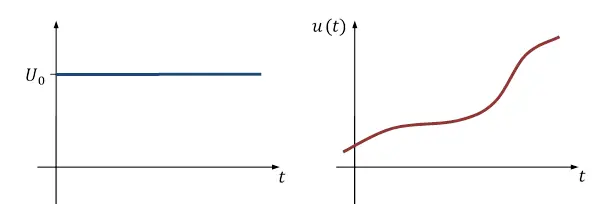
Abbildung 1-1 Gleichgröße und zeitabhängige Größe
Oft genügt es, die zeitabhängige Größe durch einige Kennwerte zu beschreiben, die ihre wichtigsten Eigenschaften enthalten.
Eine wichtige Kenngröße ist der Mittelwert in einem Intervall 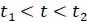 .
.
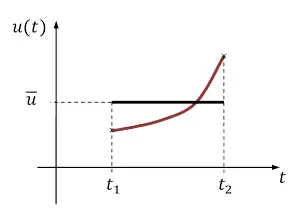
Abbildung 1-2 Mittelwert einer zeitabhängigen Größe
Der Mittelwert schließt mit der Zeitachse die gleiche Fläche ein wie der Funktionsverlauf u ( t ) in diesem Intervall:
Mittelwert ∙ Intervallbreite = Fläche unter der Kurve
Читать дальше

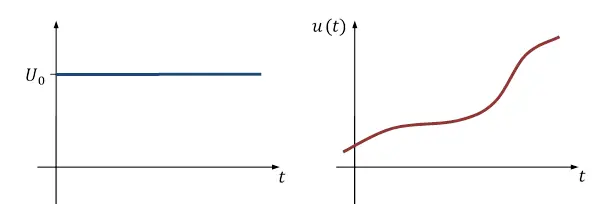
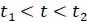 .
.











