Anthony R. West - Solid State Chemistry and its Applications

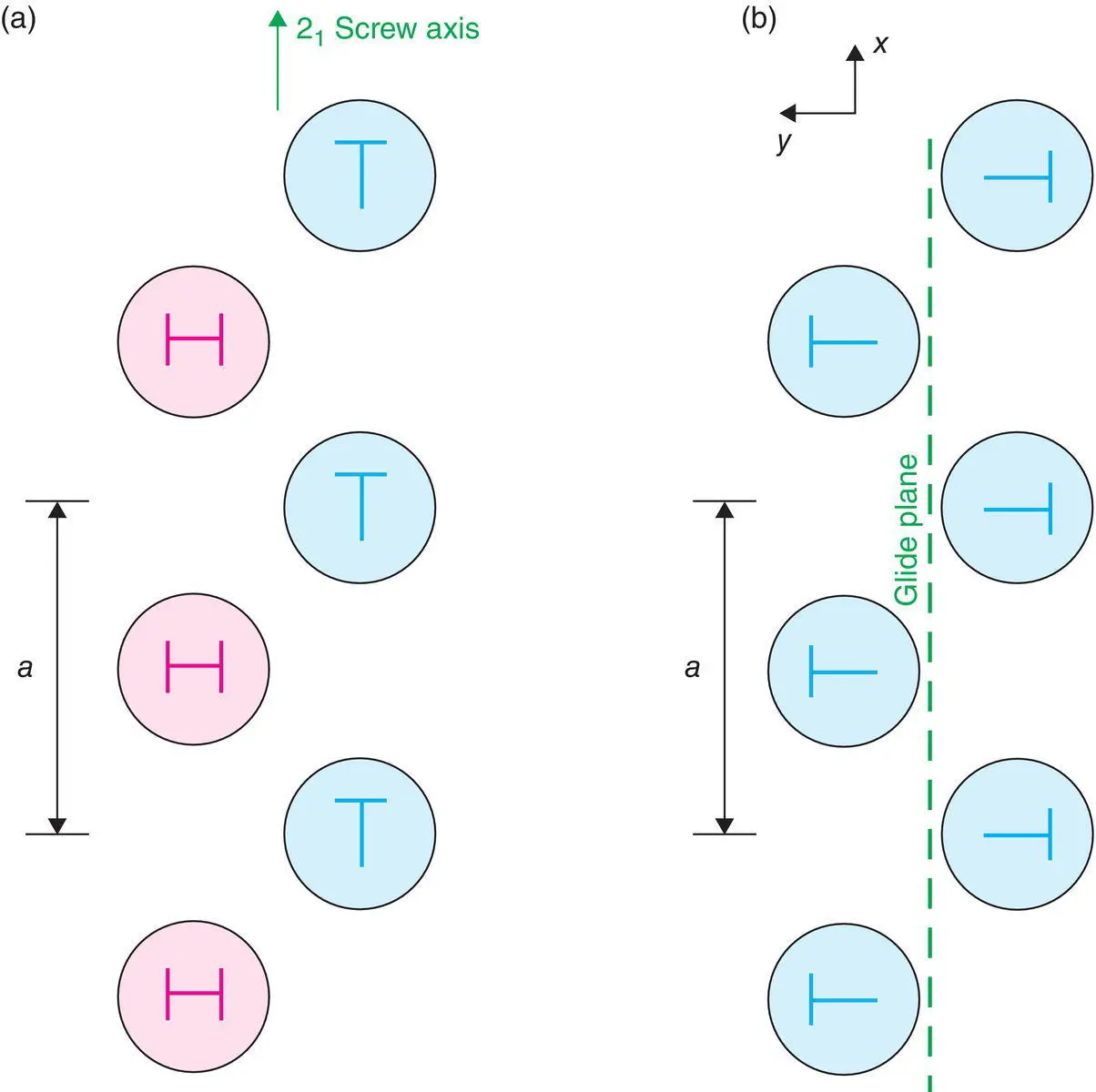
Figure 1.8 Arrangement of coins with heads (H) and tails (T) illustrating (a) a 21 screw axis parallel to a and (b) an a glide plane perpendicular to b; in each case, translation between symmetry‐related objects is by a/2.

The glide plane combines translation and reflection, as shown schematically in Fig. 1.8(b). Translation may be parallel to any of the unit cell axes ( a , b, c ), to a face diagonal ( n ) or to a body diagonal ( d ). The a, b, c and n glide planes all have a translation step of half the unit cell in that direction; by definition, the d glide has a translation step which is ¼ of the body diagonal. For the axial glide planes a, b and c , it is important to know both the direction of the translation and the reflection plane, e.g. an a glide may be perpendicular to b (i.e. reflection across the ac plane), Fig 1.8(b), or perpendicular to c .

Most crystal structures contain examples of space symmetry elements which are often difficult to visualise unless one has 3D models available. An example of both a screw axis and a glide plane in the same structure is shown in Fig 1.21 and discussed in Section 1.12. It is always amusing to look for symmetries in everyday objects. Next time you are in a car park, look at the arrangement of parking lots, especially if they are arranged diagonally, and see if they are displaced relative to each other in the form of a glide plane!

One difference between crystals and quasicrystals concerns space symmetry. Crystals, as a bare minimum, exhibit a periodic translation from one unit cell to the next. In many cases, translational symmetry elements, i.e. screw axes and glide planes, are also present. By contrast, quasicrystals do not exhibit space symmetry: they do not have a regular repeat unit, nor can translational symmetry elements be identified.

The geometric shapes of the various crystal systems (unit cells) are listed in Table 1.1 and are shown in Fig. 1.3. These shapes do not define the unit cell; they are merely a consequence of the presence of certain symmetry elements.

A cubic unit cell is defined as one having four threefold symmetry axes. These run parallel to the cube body diagonals, one of which is shown in Fig. 1.9(a); an automatic consequence of this condition is that a = b = c and α = β = γ = 90°. The essential symmetry elements by which each crystal system is defined are listed in Table 1.1. In most crystal systems, additional symmetry elements are also present. For instance, cubic crystals may have many others, including three fourfold axes passing through the centres of each pair of opposite cube faces (a) and mirror planes in two sets of orientations (b, c).

The tetragonal unit cell, Table 1.1, has a single fourfold axis and may be regarded as a cube that is either squashed or elongated along one axis. Consequently, all threefold rotation axes and two of the fourfold axes are lost. An example is given by the structure of CaC 2. This is related to the NaCl structure but, because the carbide ion is cigar‐shaped rather than spherical, one of the cell axes becomes longer than the other two, Fig. 1.10(a). A similar tetragonal cell may be drawn for NaCl; it occupies half the volume of the true, cubic unit cell, Fig. 1.10(b). The choice of a tetragonal unit cell for NaCl is rejected, however, because it does not show the full cubic symmetry, i.e. it does not show the threefold axes. A tetragonal unit cell has one axis, the unique axis, which is of a different length to the other two. By convention, this is chosen as the c axis, Table 1.1.

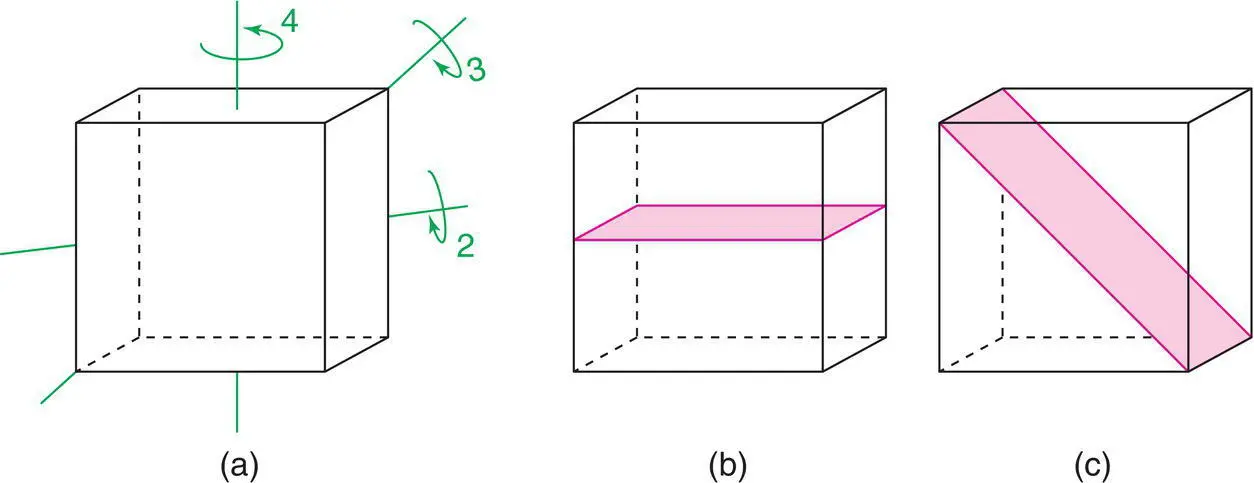
Figure 1.9 (a) Two‐, three‐ and fourfold axes and (b, c) mirror planes of a cube.

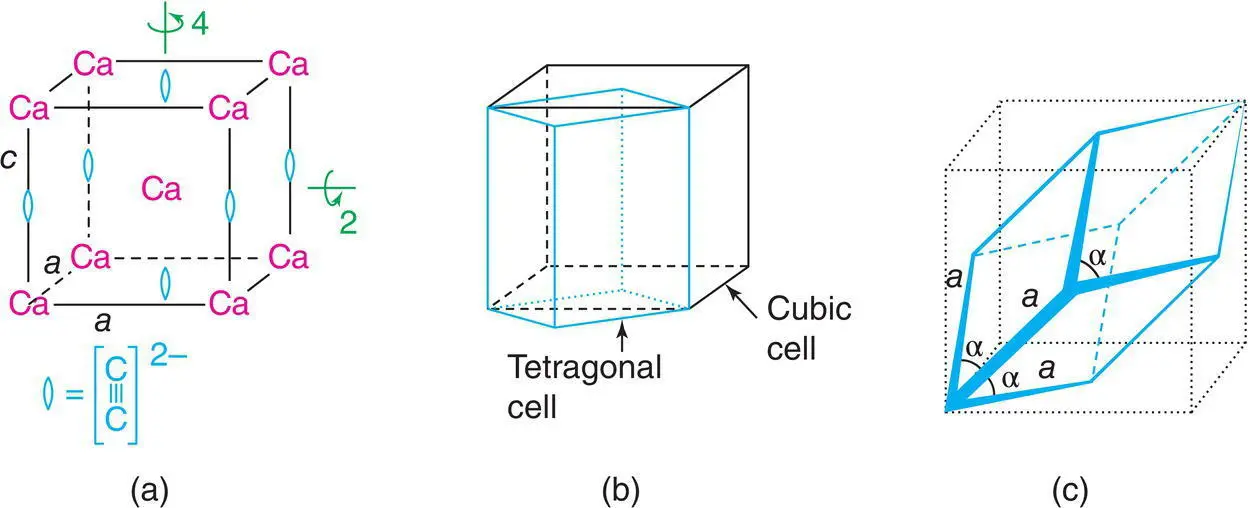
Figure 1.10 (a) Tetragonal unit cell of CaC2: note the cigar‐shaped carbide ions are aligned parallel to c; (b) relation between ‘tetragonal’ and cubic cells for NaCl; (c) derivation of a primitive trigonal unit cell for NaCl from the cubic cell.

The trigonal system is characterised by a single threefold axis. Its shape is derived from a cube by stretching or compressing the cube along one of its body diagonals, Fig. 1.10(c). The threefold axis parallel to this direction is retained but those along the other body diagonals are destroyed. All three cell edges remain the same length; all three angles stay the same but are not equal to 90°. It is possible to describe such a trigonal cell for NaCl with α = β = γ = 60° with Na at the corners and Cl in the body centre (or vice versa), but this is again unacceptable because NaCl has symmetry higher than trigonal.

The structure of NaNO 3is a trigonal distortion of the NaCl structure: instead of spherical Cl –ions, it has triangular nitrate groups. These lie on planes perpendicular to one of the unit cell body diagonals. This causes a compression along one body diagonal (or rather an expansion in the plane perpendicular to the diagonal). All fourfold symmetry axes and all but one of the threefold axes are destroyed.

The hexagonal crystal system is discussed later (Fig. 1.21).

The orthorhombic unit cell may be regarded as a shoebox in which the angles are 90° but the sides are of unequal length. It usually possesses several mirror planes and twofold axes; the minimum requirement for orthorhombic symmetry is the presence of three mutually perpendicular mirror planes or twofold axes.

The monoclinic unit cell may be derived from our orthorhombic shoebox by partially shearing the top face relative to the bottom face and in a direction parallel to one of the box edges. As a consequence, one angle departs from 90° and most of the symmetry is lost, apart from a mirror plane and/or a single twofold axis. One of the monoclinic unit cell axes is unique since it is perpendicular to the other two. The unique axis is usually defined as b , with α = γ = 90° (but see Table 1.1, footnote).

The triclinic system possesses no essential symmetry. Its unit cell has sides of unequal length and the angles are unequal and differ from 90°.

We have specified the essential symmetry elements for each crystal system. Consequently, the unit cell shapes follow automatically. The converse does not apply, however, in crystals which exhibit pseudo‐symmetry . For example, the unit cell of a particular structure may be geometrically cubic but the atomic arrangement may not exhibit the requisite symmetry elements and, instead, the true crystal system may have symmetry lower than cubic.

It is very useful to be able to represent the manner of repetition of atoms, ions or molecules in a crystal by an array of points; the array is called a lattice and the points lattice points ; each lattice point has exactly the same environment and the same arrangement of surrounding atoms. The section of the NaCl structure shown in Fig. 1.11(a) may be represented by an array of points (b); each point represents one Na and one Cl but whether the point is located at Na, at Cl, or in between is irrelevant. The unit cell is constructed by linking the lattice points; two ways of doing this, A and B, are shown in (b). A cell such as B which has lattice points only at the corners is primitive, P, whereas a cell such as A which has additional lattice points is centred . Several types of centred lattice are possible.