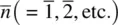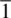Anthony R. West - Solid State Chemistry and its Applications

b The symbol ≠ means ‘not necessarily equal to’. Sometimes, crystals possess pseudo‐symmetry . For example, a unit cell may be geometrically cubic but not possess the essential symmetry elements for cubic symmetry; the true symmetry is then lower, perhaps tetragonal.

The seven crystal systems listed in Table 1.1 and shown in Fig. 1.3 are the seven independent unit cell shapes that are possible in three‐dimensional (3D) crystal structures. Six of these unit cell shapes are closely inter‐related and are either cubic or can be derived by distorting a cube in various ways, as shown in Fig. 1.3(b).

Thus, if one axis, c , is of different length to the others, the shape is tetragonal; if all three axes are different, the shape is orthorhombic . If, now, one of the angles, β , is not 90°, the shape is monoclinic, whereas if all three angles differ from 90°, the shape is triclinic . Finally, if the cube is stretched, or compressed, along a body diagonal so that all three angles remain equal, but different from 90°, the shape is trigonal .

The remaining unit cell shape is hexagonal . A hexagonal‐shaped box is shown in Fig. 1.3(a) and discussed later with reference to Fig. 1.21, but the true unit cell is only one‐third of this size, as shown.

Although it is common practice to describe unit cells by their shapes, it is more correct to describe them by the presence or absence of symmetry. Thus, for example, if a unit cell has four intersecting threefold axes, it must be cubic in shape; the reverse does not necessarily apply and the unit cell could be fortuitously cubic but not have the threefold symmetries in the atomic arrangements. The essential symmetry for each crystal system is given in the third column of Table 1.1. Let us deal next with symmetry.

Symmetry is most easily defined using examples. Consider the silicate tetrahedron shown in Fig. 1.4(a). If it is rotated about an axis passing along the vertical Si–O bond, then every 120° the tetrahedron finds itself in an identical position. Effectively, the three basal oxygens change position with each other every 120°. During a complete 360° rotation, the tetrahedron passes through three identical positions. The fact that different (i.e. >1) identical orientations are possible means that the SiO 4tetrahedron possesses symmetry. The axis about which the tetrahedron may be rotated is called a rotation axis; it is an example of a symmetry element . The process of rotation is an example of a symmetry operation .

Figure 1.3 (a) The seven crystal systems and their unit cell shapes; (b) five of the seven crystal systems can be derived from cubic by structural distortions.

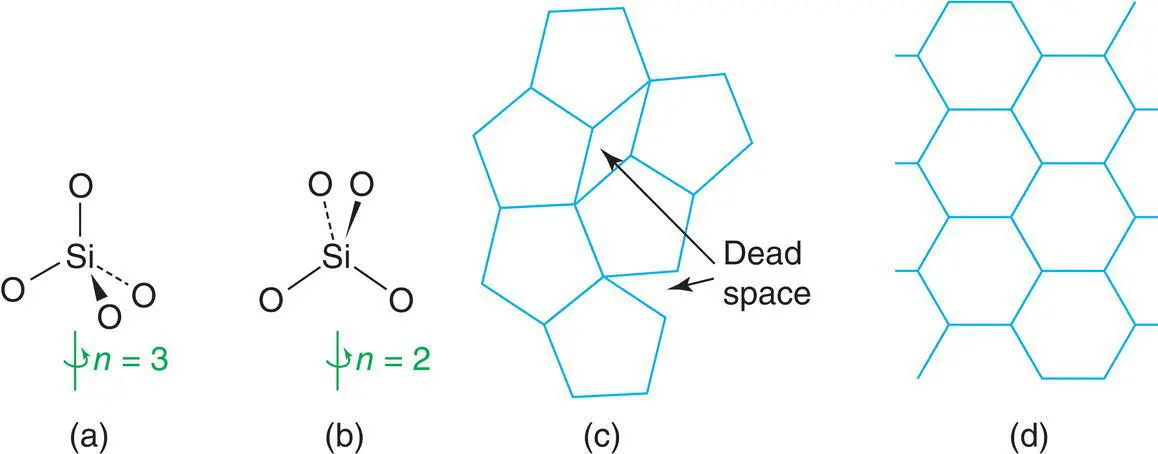
Figure 1.4 (a) Threefold and (b) twofold rotation axes; (c) the impossibility of forming a complete layer of pentagons; (d) a complete layer of hexagons.

The symmetry elements that are important in crystallography are listed in Table 1.2. There are two nomenclatures for labelling them, the Hermann–Mauguin system used in crystallography and the Schönflies system used in spectroscopy. Ideally, there would be only one system which everybody uses, but this is unlikely to come about since (a) both systems are very well established, (b) crystallographers require elements of space symmetry that spectroscopists do not and vice versa, (c) spectroscopists use a more extensive range of point symmetry elements than crystallographers.

The symmetry element described above for the silicate tetrahedron is a rotation axis, with symbol n . Rotation about this axis by 360/ n degrees gives an identical orientation and the operation is repeated n times before the original configuration is regained. In this case, n = 3 and the axis is a threefold rotation axis . The SiO 4tetrahedron possesses four threefold rotation axes, one in the direction of each Si–O bond.

When viewed from another angle, SiO 4tetrahedra possess twofold rotation axes [Fig. 1.4(b)] which pass through the central Si and bisect the O–Si–O bonds. Rotation by 180° leads to indistinguishable orientations of the tetrahedra. The SiO 4tetrahedron possesses three of these twofold axes.

Crystals may display rotational symmetries 2, 3, 4 and 6. Others, such as n = 5, 7, are never observed in 3D crystal structures based on a regular periodic repetition of the unit cell and its contents. This is shown in Fig. 1.4(c), where a fruitless attempt has been made to pack pentagons to form a complete layer; thus, individual pentagons have fivefold symmetry but the array of pentagons does not. For hexagons with sixfold rotation axes (d), a complete layer is easily produced; both the individual hexagons and the overall array exhibit sixfold symmetry. This is not to say that molecules that have pentagonal symmetry, n = 5, cannot exist in the crystalline state. They can, of course, but their fivefold symmetry cannot be exhibited by the crystal as a whole.

Table 1.2 Symmetry elements

	Symmetry element	Hermann–Mauguin symbols (crystallography)	Schönflies symbols (spectroscopy)
Point symmetry	Mirror plane	m	σ v, σ h
	Rotation axis	n = 2, 3, 4, 6	C n( C 2, C 3, etc.)
	Inversion axis		–
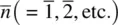	Alternating axis a	–	S n( S 1, S 2, etc.)
	Centre of symmetry		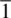i
Space symmetry	Glide plane	a , b , c , d , n	–
	Screw axis	2 1, 3 1, etc.	–

a The alternating axis is a combination of rotation ( n ‐fold) and reflection perpendicular to the rotation axis. It is little used in crystallography.

The discovery of a new state of matter, the quasicrystalline state, by Schechtman and colleagues, published in 1984 (and which led to the Nobel Prize in Chemistry in 2011) appeared at first sight to violate the rules concerning allowable rotational symmetries in crystal lattices. From their single‐crystal diffraction patterns, rotational symmetries such as n = 5 but also n = 10 and 12 were observed whereas, as shown in Fig. 1.4(c), a regular crystal lattice exhibiting fivefold rotational symmetry cannot exist. The answer to this conundrum is that quasicrystals do not have regularly repeating crystal structures based on a single unit cell motif. Instead, they have fully ordered but non‐periodic arrays constructed from more than one motif or building block.

Elegant examples of quasisymmetry are found in so‐called Penrose tiling, as shown in Fig. 1.5. In this example, space is filled completely by a combination of red and blue diamonds; such a tiling pattern has many local areas of fivefold symmetry but the structure as a whole is not periodic, does not exhibit fivefold symmetry and a regular repeat unit cannot be identified. Quasicrystals have since been discovered in a wide range of alloy systems and also in organic polymer and liquid crystal systems; they have been discovered in Nature in an Al–Cu–Fe alloy named icosahedrite that was believed to have been part of a meteorite and had existed on Earth for billions of years. It is probably just a matter of time before they are discovered also in inorganic oxide materials, natural or synthetic.