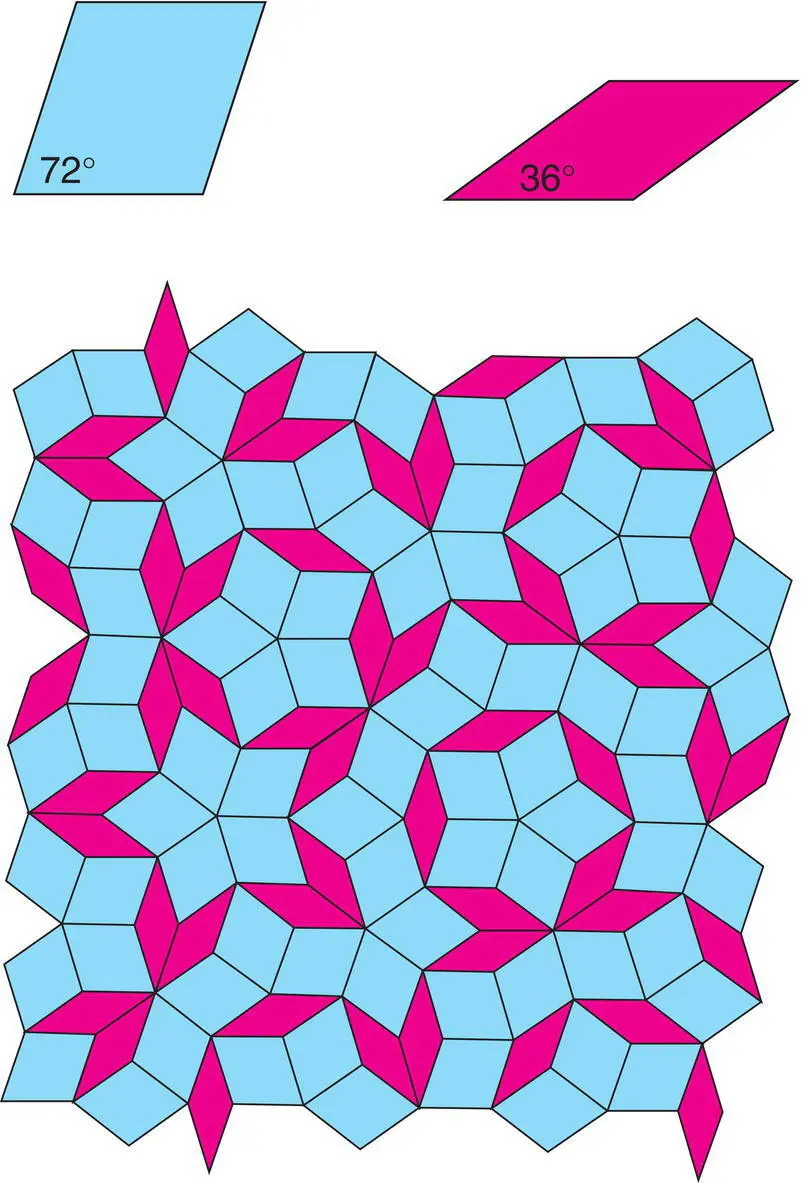
Figure 1.5 Two‐dimensional Penrose tiling constructed by packing together two different sets of parallelograms. C. Janot, Quasicrystals: A Primer, Oxford University Press (1997). Penrose was co‐recipient of the 2020 Nobel Prize in physics, in a totally different area to quasicrystals and Penrose tiling, for ‘discovery that black hole formation is a robust prediction of the general theory of relativity’.
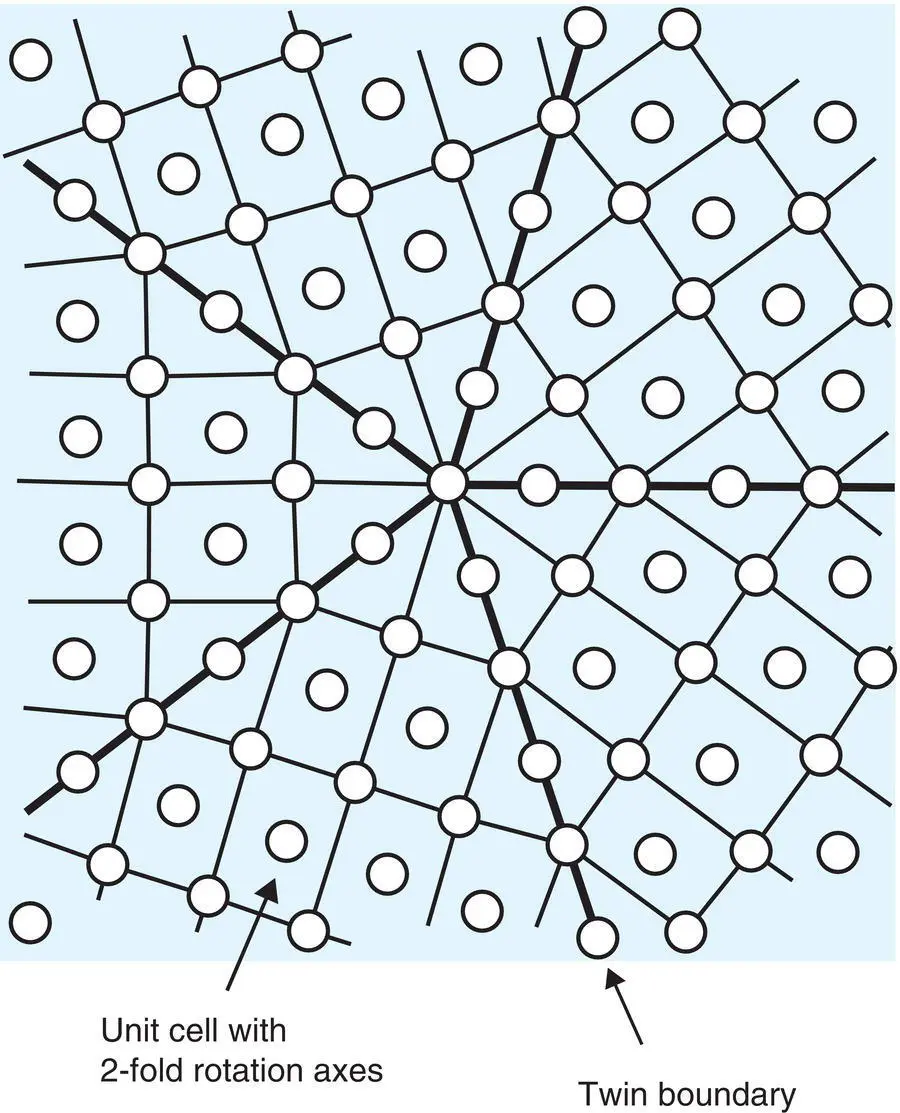
Figure 1.6 Hypothetical twinned structure showing fivefold symmetry.
Adapted from J. M. Dubois, Useful Quasicrystals, World Scientific Publishing Company (2005).
In the early days of work on quasicrystals, an alternative explanation for possible fivefold symmetry was based on twinning, as shown schematically in Fig. 1.6. Five identical crystalline segments are shown, each of which has twofold rotational symmetry in projection. Pairs of crystal segments meet at a coherent interface or twin plane in which the structures on either side of the twin plane are mirror images of each other. The five crystal segments meet at a central point which exhibits fivefold symmetry as a macroscopic element of point symmetry but the individual crystal segments clearly do not exhibit any fivefold symmetry. Schechtman showed conclusively that twinning such as shown in Fig. 1.6 could not explain the quasicrystalline state.
The discovery of quasicrystals without long range periodicity and an identifiable unit cell, has forced the International Union of Crystallography to reconsider what is meant by a ‘crystal’. Since well‐prepared quasicrystals have highly ordered structures, many of which are thermodynamically stable and give sharp single crystal diffraction patterns, quasicrystals need to have a home in a wider definition of crystallinity. The requirement for crystallinity to be associated with long range periodicity has served the scientific community well for nearly a century; however, it is now necessary to include quasicrystals that are highly ordered but lack long range periodicity. The terms ‘classical crystal’ and ‘aperiodic crystal’ have been suggested to distinguish between crystals that do, and do not, exhibit long range periodicity.
The consequences that aperiodicity within ordered structures has for the electronic structure and optoselectronic properties of quasicrystals are still being evaluated. Periodicity has provided an important starting point in the development of theoretical concepts such as Brillouin zones and the band theory of solids. It has also underpinned theories of dislocations and explanations about the mechanical properties of crystalline materials, especially metals and alloys. However, it is probably fair to say that, at present, although quasicrystals are much more than a scientific curiosity, they do not, as yet, fit into the general panorama of mainstream solid state sciences, perhaps because of the challenges and difficulties associated with evaluating and presenting aperiodic crystallography in terms of higher dimensional space.
A mirror plane, m, exists when two halves of, for instance, a molecule can be interconverted by carrying out the imaginary process of reflection across the mirror plane. The silicate tetrahedron possesses six mirror planes, one of which, running vertically and perpendicular to the plane of the paper, is shown in Fig. 1.7(a). The silicon and two oxygens, 1 and 2, lie on the mirror plane and are unaffected by reflection. The other two oxygens, 3 and 4, are interchanged on reflection. A second mirror plane lies in the plane of the paper; for this, Si and oxygens 3, 4 lie on the mirror but oxygen 2, in front of the mirror, is the image of oxygen 1, behind the mirror.
The photograph in Fig. 1.7(d) shows the British comedian Harry Worth creating a mirror image of half of his body by posing at the end of a high street shop window. Half of the picture is of his body and half is its mirror image. It therefore exhibits perfect mirror symmetry which is never achieved by human bodies in reality!
1.2.4 Centre of symmetry and inversion axes
A centre of symmetry , 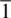 , exists when any part of a structure can be reflected through this centre of symmetry, which is a point and an identical arrangement found on the other side. An AlO 6octahedron has a centre of symmetry, Fig. 1.7(b), located on the Al atom. If a line is drawn from any oxygen, e.g. 1, through the centre and extended an equal distance on the other side, it terminates at another oxygen, 2. A tetrahedron, e.g. SiO 4, does not have a centre of symmetry (a).
, exists when any part of a structure can be reflected through this centre of symmetry, which is a point and an identical arrangement found on the other side. An AlO 6octahedron has a centre of symmetry, Fig. 1.7(b), located on the Al atom. If a line is drawn from any oxygen, e.g. 1, through the centre and extended an equal distance on the other side, it terminates at another oxygen, 2. A tetrahedron, e.g. SiO 4, does not have a centre of symmetry (a).
The inversion axis,  , is a combined symmetry operation involving rotation (according to n ) and inversion through the centre. A
, is a combined symmetry operation involving rotation (according to n ) and inversion through the centre. A  ( fourfold inversion ) axis is shown in (c). The first stage involves rotation by 360/4 = 90° and takes, for example, oxygen 2 to position 2′. This is followed by inversion through the centre, at Si, and leads to position 3. Oxygens 2 and 3 are therefore related by a
( fourfold inversion ) axis is shown in (c). The first stage involves rotation by 360/4 = 90° and takes, for example, oxygen 2 to position 2′. This is followed by inversion through the centre, at Si, and leads to position 3. Oxygens 2 and 3 are therefore related by a 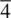 axis. Possible inversion axes in crystals are limited to
axis. Possible inversion axes in crystals are limited to 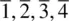 and
and 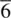 for the same reason that only certain pure rotation axes are allowed. The onefold inversion axis is not a separate symmetry element, but is simply equivalent to the centre of symmetry; also, the twofold inversion axis is the same as a mirror plane perpendicular to that axis.
for the same reason that only certain pure rotation axes are allowed. The onefold inversion axis is not a separate symmetry element, but is simply equivalent to the centre of symmetry; also, the twofold inversion axis is the same as a mirror plane perpendicular to that axis.
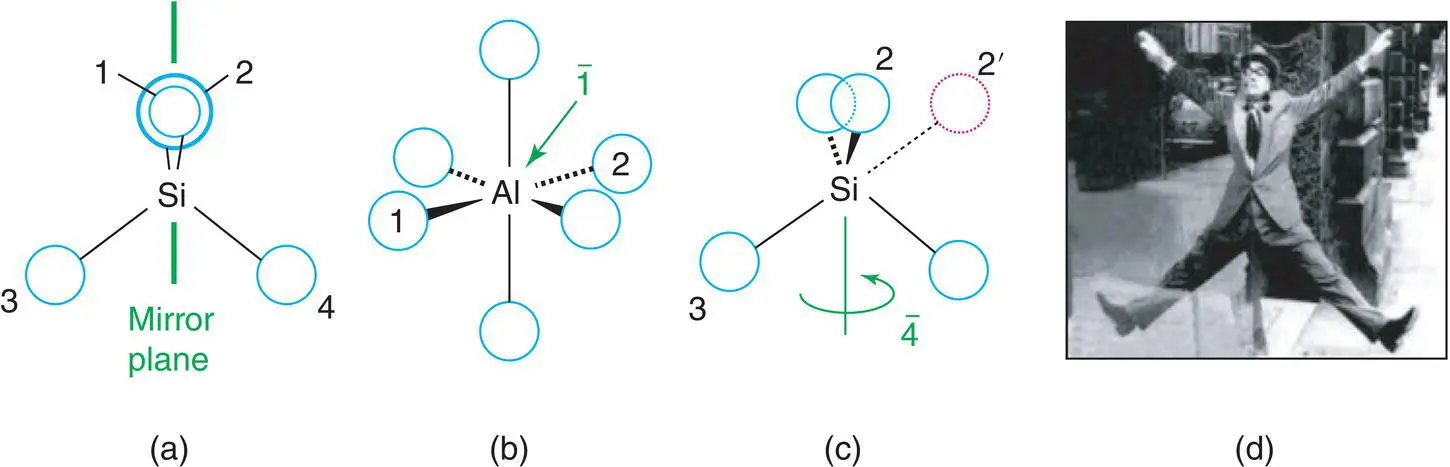
Figure 1.7 Symmetry elements: (a) mirror plane; (b) centre of symmetry; (c) fourfold inversion axis. (d) The British comedian Harry Worth creating a mirror image of half of his body by reflection in a shop window.
1.2.5 Point symmetry and space symmetry
The symmetry elements discussed so far are elements of point symmetry . For each, at least one point stays unchanged during the symmetry operation, i.e. an atom lying on a centre of symmetry, rotation axis or mirror plane does not move during the respective symmetry operations. Finite‐sized molecules can only possess point symmetry elements, whereas crystals may have extra symmetries that include translation steps as part of the symmetry operation. These are elements of space symmetry, of which there are two types.
The screw axis combines translation and rotation; the atoms or ions in a crystal which possesses screw axes appear to lie on spirals about these axes. A schematic example is shown in Fig. 1.8(a). All you need to demonstrate a screw axis is a handful of coins which can be arranged on a flat surface with either their heads (H) or tails (T) facing upwards. The symbol for a screw axis, X Y, indicates translation by the fraction Y/X of the unit cell edge in the direction of the screw axis together with simultaneous rotation by 360/X° about the screw axis. Thus, a 4 2axis parallel to a involves translation by a /2 and rotation by 90°; this process takes place twice along a for every unit cell.
Читать дальше



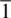 , exists when any part of a structure can be reflected through this centre of symmetry, which is a point and an identical arrangement found on the other side. An AlO 6octahedron has a centre of symmetry, Fig. 1.7(b), located on the Al atom. If a line is drawn from any oxygen, e.g. 1, through the centre and extended an equal distance on the other side, it terminates at another oxygen, 2. A tetrahedron, e.g. SiO 4, does not have a centre of symmetry (a).
, exists when any part of a structure can be reflected through this centre of symmetry, which is a point and an identical arrangement found on the other side. An AlO 6octahedron has a centre of symmetry, Fig. 1.7(b), located on the Al atom. If a line is drawn from any oxygen, e.g. 1, through the centre and extended an equal distance on the other side, it terminates at another oxygen, 2. A tetrahedron, e.g. SiO 4, does not have a centre of symmetry (a). , is a combined symmetry operation involving rotation (according to n ) and inversion through the centre. A
, is a combined symmetry operation involving rotation (according to n ) and inversion through the centre. A  ( fourfold inversion ) axis is shown in (c). The first stage involves rotation by 360/4 = 90° and takes, for example, oxygen 2 to position 2′. This is followed by inversion through the centre, at Si, and leads to position 3. Oxygens 2 and 3 are therefore related by a
( fourfold inversion ) axis is shown in (c). The first stage involves rotation by 360/4 = 90° and takes, for example, oxygen 2 to position 2′. This is followed by inversion through the centre, at Si, and leads to position 3. Oxygens 2 and 3 are therefore related by a 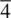 axis. Possible inversion axes in crystals are limited to
axis. Possible inversion axes in crystals are limited to 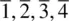 and
and 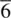 for the same reason that only certain pure rotation axes are allowed. The onefold inversion axis is not a separate symmetry element, but is simply equivalent to the centre of symmetry; also, the twofold inversion axis is the same as a mirror plane perpendicular to that axis.
for the same reason that only certain pure rotation axes are allowed. The onefold inversion axis is not a separate symmetry element, but is simply equivalent to the centre of symmetry; also, the twofold inversion axis is the same as a mirror plane perpendicular to that axis.











