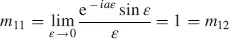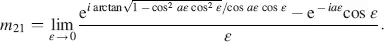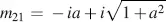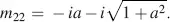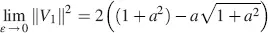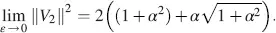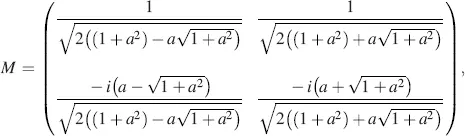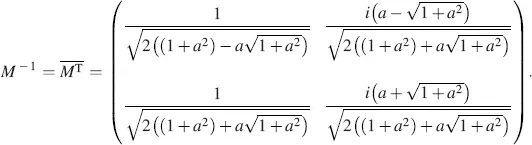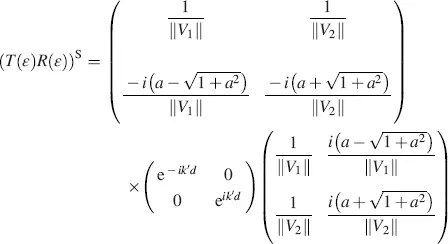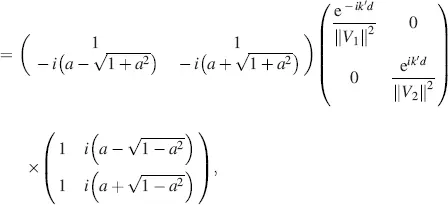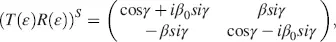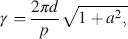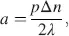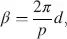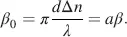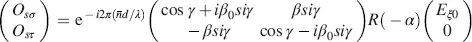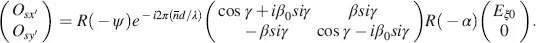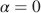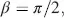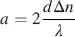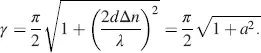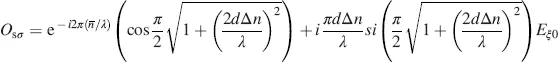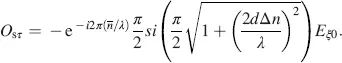The limit of M in Equation (4.31)is calculated in the following steps with φ = arctan 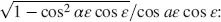 as the elements mik in the unnormalized matrix M in Equation (4.28)and the magnitudes in Equations (4.29)and (4.30)tend to zero for ε → 0, we choose r 1= r 21/ ε and evaluate the limits of the numerator and denominator in Equation (4.31)separately according to Hopital’s rule. By doing so, we obtain for the numerators
as the elements mik in the unnormalized matrix M in Equation (4.28)and the magnitudes in Equations (4.29)and (4.30)tend to zero for ε → 0, we choose r 1= r 21/ ε and evaluate the limits of the numerator and denominator in Equation (4.31)separately according to Hopital’s rule. By doing so, we obtain for the numerators
(4.38) 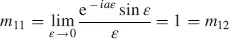
and
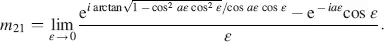
With similar calculations as performed for D , we obtain the limit as
(4.39) 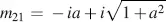
and in the same way, also
(4.40) 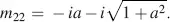
For the magnitudes the evaluation of the limit value is performed at the square of the magnitudes in Equations (4.29)and (4.30), again leading with similar calculations as for D to
(4.41) 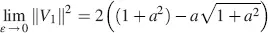
and
(4.42) 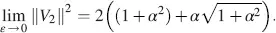
Hence, the normalized M is, for ε → 0,
(4.43) 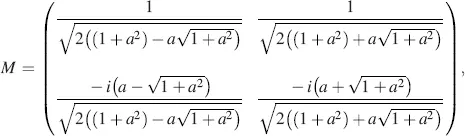
from which, as M is a unitary matrix, we obtain
(4.44) 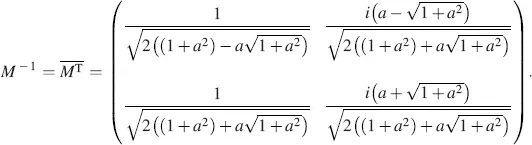
Inserting Equations (4.29), (4.30), (4.43)and (4.44)into Equation (4.28)provides, for ε → 0,
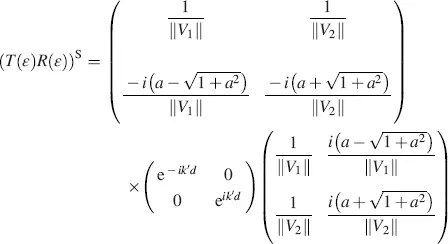
(4.45) 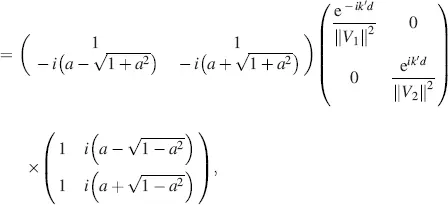
with k ′ in Equation (4.36). Performing the multiplications in Equation (4.45)results in
(4.46) 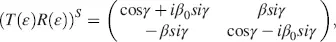
with
(4.47) 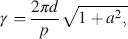
(4.48) 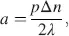
(4.49) 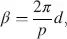
and
(4.50) 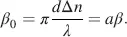
The final result is, with Equation (4.15),
(4.51) 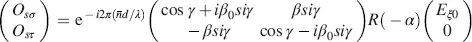
given in the σ – τ coordinates in Figure 4.1, which are rotated by the twist angle − β from the x – y coordinates. An evaluation of the results in the x ′ – y ′ coordinates in Figure 4.1requires a rotation by the angle ψ , resulting in
(4.52) 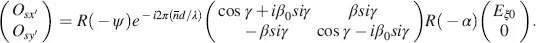
This result will be discussed for three special cases, namely the Twisted Nematic cell (TN cell) with α = 0 and β = π /2, the Supertwist TN cell (STN-cell) with α = 0 and β > π /2 and the Mixed mode TN cell (MTN-cell) with α ≠ 0 and β ≠ π /2.
The derivation of Equation (4.52)also contains a proof of the Chebychev identity. The full length of the derivation was presented in a detailed manner, as it leads to a core result for LCDs. Further, the considerations involved are useful for solving a variety of special display problems.
4.2 The Various Types of TN Cells
4.2.1 The regular TN cell
This cell is the most widely used active matrix LCD(Schadt and Helfrich, 1971; Yeh, 1988), and represents a special case of the general result in Equation (4.51). The linearly polarized light is incident at an angle
(4.53) 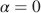
in Figure 4.1that is parallel to the director of the LC molecules on top of the orientation layer. The twist angle is
(4.54) 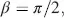
leading to a pitch in Equation (4.49)of p = 4 d . Hence, at z = d the helix has reached a quarter of a turn. From these values follow a in Equation (4.48)as
(4.55) 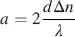
and γ in Equation (4.47)as
(4.56) 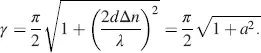
In Equation (4.51), the σ -axis is rotated by β = π /2 from the x -axis, whereas the τ -axis is parallel to the x -axis. The Jones vectors in the σ - τ axes assume, after insertion of Equations (4.54), (4.55)and (4.56)into Equation (4.51), the form
(4.57) 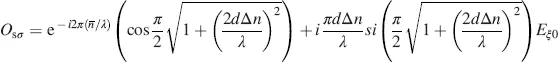
and
(4.58) 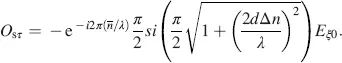
For parallel polarizers the analyser lies in the τ -axis. The intensity Iτ passing this analyser is (Gooch and Tarry, 1974)
Читать дальше

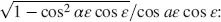 as the elements mik in the unnormalized matrix M in Equation (4.28)and the magnitudes in Equations (4.29)and (4.30)tend to zero for ε → 0, we choose r 1= r 21/ ε and evaluate the limits of the numerator and denominator in Equation (4.31)separately according to Hopital’s rule. By doing so, we obtain for the numerators
as the elements mik in the unnormalized matrix M in Equation (4.28)and the magnitudes in Equations (4.29)and (4.30)tend to zero for ε → 0, we choose r 1= r 21/ ε and evaluate the limits of the numerator and denominator in Equation (4.31)separately according to Hopital’s rule. By doing so, we obtain for the numerators