Similarity graphs: There are several popular constructions to transform a given set x 1, …, x nof data points with pairwise similarities s ijor pairwise distances d ijinto a graph. When constructing similarity graphs, the goal is to model the local neighborhood relationships between the data points.
The ε‐neighborhood graph: Here, we connect all points whose pairwise distances are smaller than ε. As the distances between all connected points are roughly of the same scale (at most ε), weighting the edges would not incorporate more information about the data to the graph. Hence, the ε‐neighborhood graph is usually considered an unweighted graph.
k ‐nearest neighbor graphs: Here, the goal is to connect vertex v iwith vertex v jif v jis among the k‐nearest neighbors of v i. However, this definition leads to a directed graph, as the neighborhood relationship is not symmetric. There are two ways of making this graph undirected. The first way is to simply ignore the directions of the edges, that is, we connect v iand v jwith an undirected edge if v iis among the k‐nearest neighbors of v jor if v jis among the k‐nearest neighbors of v i. The resulting graph is what is usually called the k‐nearest neighbor graph. The second choice is to connect vertices v iand v jif both of the following are true: (i) v iis among the k‐nearest neighbors of v jand (ii) v jis among the k‐nearest neighbors of v i. The resulting graph is called the mutual k‐nearest neighbor graph. In both cases, after connecting the appropriate vertices, we weight the edges by the similarity of their endpoints.
The fully connected graph : Here, we simply connect all points with positive similarity with each other, and we weight all edges by s ij. As the graph should represent the local neighborhood relationships, this construction is useful only if the similarity function itself models local neighborhoods. An example of such a similarity function is the Gaussian similarity function s(x i, x j) = exp (−‖x i− x j‖ 2/(2σ 2)), where the parameter σ controls the width of the neighborhoods. This parameter plays a similar role as the parameter ε in the case of the ε‐neighborhood graph.
Graph Laplacians : The main tools for spectral clustering are graph Laplacian matrices. There exists a whole field dedicated to the study of those matrices, called spectral graph theory. In this section, we want to define different graph Laplacians and point out their most important properties. Note that in the literature there is no unique convention that governs exactly which matrix is called “graph Laplacian.” Usually, every author just calls “his” matrix the graph Laplacian. Hence, a lot of care is needed when reading the literature on graph Laplacians.
In the following, we always assume that G is an undirected, weighted graph with weight matrix W, where w ij= w ji≥ 0. When using the eigenvectors of a matrix, we will not necessarily assume that they are normalized. For example, the constant vector 1 and a multiple a1 for some a ≠ 0 will be considered the same eigenvectors. Eigenvalues will always be ordered in ascending order, respecting multiplicities. By “the first k eigenvectors” we refer to the eigenvectors corresponding to the k smallest eigenvalues.
The unnormalized graph Laplacian is defined as L = D − W .
The following proposition summarizes the most important facts needed for spectral clustering.
(Properties of L ) The matrix L satisfies the following properties:
1 For every vector f ∈ ℝn we have
2 L is symmetric and positive semidefinite.
3 The smallest eigenvalue of L is 0, and the corresponding eigenvector is the constant one vector 1.
4 L has n non‐negative, real‐valued eigenvalues 0 = λ1 ≤ λ2≤… ≤λn.
Proof:
Part (1): By the definition of d i,
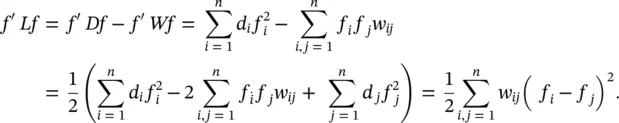
Part (2): The symmetry of L follows directly from the symmetry of W and D . The positive semidefiniteness is a direct consequence of Part (1), which shows that f ’ Lf ≥ 0 for all f ∈ ℝ n.
Part (3): Self‐evident.
Part (4) is a direct consequence of Parts (1)–(3).
The normalized graph Laplacians: There are two matrices that are called normalized graph Laplacians in the literature. Both matrices are closely related to each other and are defined as
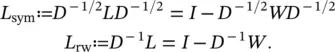
We denote the first matrix by L symas it is a symmetric matrix, and the second one by L rwas it is closely related to a random walk. In the following, we summarize several properties of L symand L rw.
(Properties of L symand L rw) The normalized Laplacians satisfy the following properties:
1 For every f ∈ ℝn we have
2 λ is an eigenvalue of Lrw with eigenvector u if and only if λ is an eigenvalue of Lsym with eigenvector w = D1/2 u.
3 λ is an eigenvalue of Lrw with eigenvector u if and only if λ and u solve the generalized eigen problem Lu = λDu.
4 0 is an eigenvalue of Lrw with the constant one vector I as eigenvector. 0 is an eigenvalue of Lsym with eigenvector D1/2I.
5 Lsym and Lrw are positive semidefinite and have n non‐negative real‐valued eigenvalues 0 = λ1≤,….≤λn.
Proof. Part (1) can be proved similarly to Part (1) of Proposition 5.1.
Part (2) can be seen immediately by multiplying the eigenvalue equation L sym w = λw with D −1/2from the left and substituting u = D −1/2 w .
Part (3) follows directly by multiplying the eigenvalue equation L rw u = λu with D from the left.
Part (4): The first statement is obvious as L rwI = 0, the second statement follows from (2).
Part (5): The statement about L symfollows from (1), and then the statement about L rwfollows from (2).
Part (5): The statement about L symfollows from (1), and then the statement about L rwfollows from (2).
Appendix 5.B Graph Fourier Transform
Graph signals : A graph signal is a collection of values defined on a complex and irregular structure modeled as a graph. In this appendix, a graph is represented as 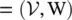 , where
, where 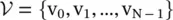 is the set of vertices (or nodes) and W is the weight matrix of the graph in which an element w ijrepresents the weight of the directed edge from node j to node i. A graph signal is represented as an
is the set of vertices (or nodes) and W is the weight matrix of the graph in which an element w ijrepresents the weight of the directed edge from node j to node i. A graph signal is represented as an
N‐dimensional vector f = [f(1), f(2), …, f(N)] T∈ ℂ N, where f(i) is the value of the graph signal at node i and 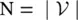 is the total number of nodes in the graph.
is the total number of nodes in the graph.
Читать дальше

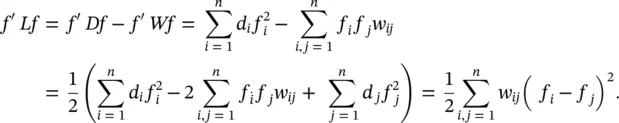
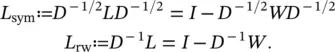
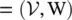 , where
, where 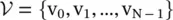 is the set of vertices (or nodes) and W is the weight matrix of the graph in which an element w ijrepresents the weight of the directed edge from node j to node i. A graph signal is represented as an
is the set of vertices (or nodes) and W is the weight matrix of the graph in which an element w ijrepresents the weight of the directed edge from node j to node i. A graph signal is represented as an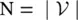 is the total number of nodes in the graph.
is the total number of nodes in the graph.










