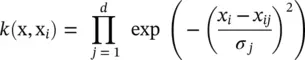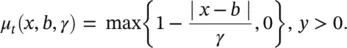Implicit mapping via kernels: Clearly this approach is not feasible, and we have to find a computationally cheaper way. The key observation [96] is that for the feature map of the above example we have
(4.54) 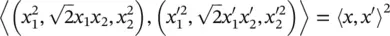
As noted in the previous section, the SV algorithm only depends on the dot products between patterns x i. Hence, it suffices to know k ( x , x ′) ≔ 〈 Φ ( x ), Φ ( x ′)〉 rather than Φ explicitly, which allows us to restate the SV optimization problem:
(4.55) 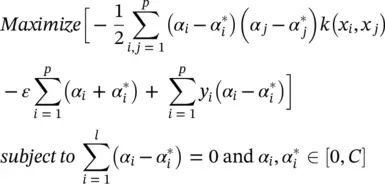
Now the expansion for f in Eq. (4.50)may be written as  and
and
(4.56) 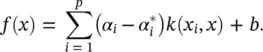
The difference to the linear case is that w is no longer given explicitly. Also, note that in the nonlinear setting, the optimization problem corresponds to finding the flattest function in the feature space, not in the input space.
4.4.3 Combination of Fuzzy Models and SVR
Given observation data from an unknown system, data‐driven methods aim to construct a decision function f (x) that can serve as an approximation of the system. As seen from the previous sections, both fuzzy models and SVR are employed to describe the decision function. Fuzzy models characterize the system by a collection of interpretable if‐then rules, and a general fuzzy model that consists of a set of rules with the following structure will be used here:
(4.57) 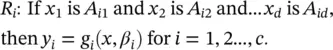
Here, parameter d is the dimension of the antecedent variables x = [ x 1, x 2, … , x d] T, R iis the i‐ th rule in the rule base, and A i1, … , A ipxare fuzzy sets defined for the respective antecedent variable. The rule consequent g i(x, β i) is a function of the inputs with parameters β i. Parameter c is the number of fuzzy rules. By modification of Eq. (4.41)to product form and Eq. (4.43), the decision function in terms of the fuzzy model by fuzzy mean defuzzification becomes
(4.58) 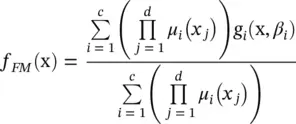
where 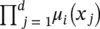 is the antecedent firing strength, and μ i( x j) is the membership of x jin the fuzzy set A i1. By the generalization of Eqs. (4.46)and (4.56), SVR is formulated as minimization of the following functional:
is the antecedent firing strength, and μ i( x j) is the membership of x jin the fuzzy set A i1. By the generalization of Eqs. (4.46)and (4.56), SVR is formulated as minimization of the following functional:
(4.59) 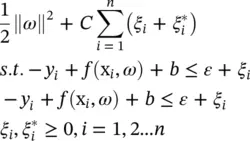
where C is the regularization parameter. The solution of (4.59)is used to determine the decision function f (x), and is given by (see Eq. (4.56)):
(4.60) 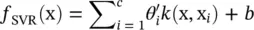
where 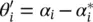 are subjected to constraints 0 ≤ α i,
are subjected to constraints 0 ≤ α i, 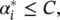 c is the number of support vectors, and the kernel k (x, x i) = 〈 Φ (x), Φ (x i)〉 is an inner product of the images in the feature space. The model given by Eq. (4.60)is referred to as the SVR model.
c is the number of support vectors, and the kernel k (x, x i) = 〈 Φ (x), Φ (x i)〉 is an inner product of the images in the feature space. The model given by Eq. (4.60)is referred to as the SVR model.
Motivated by the underlying concept of granularity, both the kernel in Eq. (4.60)and the fuzzy membership function in Eq. (4.59)are information granules. The kernel is a similarity measure between the support vector and the non‐support vector in SVR, and fuzzy membership functions associated with fuzzy sets are essentially linguistic granules, which can be viewed as linked collections of fuzzy variables drawn together by the criterion of similarity. Hence, [97–99] regarded kernels as the Gaussian membership function of the t‐norm‐based algebra product
(4.61) 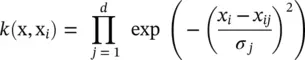
and incorporated SVR in FM. In Eq. (4.61), x i= [ x i1, x i2, . . . x id] Tdenotes the support vector in the framework of SVR, but x ijis referred as to the center of the Gaussian membership function. Parameter σ jis a hyperparameter of the kernel, whereas it represents the dispersion of the Gaussian membership function in fuzzy set theory.
Fuzzy model based on SVR : Combining the fuzzy model with SVR, we can build a fuzzy system that can use the advantages that each technique offers, so the trade‐off could be well balanced under this combination. Such a model is developed to extract support vectors for generating fuzzy rules, so c is equal in both Eqs. (4.58)and (4.60). Sometimes there are too many support vectors, which will lead to a redundant and complicated rule base even though the model performance is good. Alternatively, we could reduce the number of support vectors and utilize them to generate a transparent fuzzy model. Simultaneously, we make the fuzzy model retain the original performance of the SVR model, and learn the experience already acquired from SVR. In such a way, an experience‐oriented learning algorithm is created. So, a simplification algorithm is employed to obtain reduced‐set vectors instead of support vectors for constructing the fuzzy model, and the parameters are adjusted by a hybrid learning mechanism considering the experience of the SVR model on the same training data set. The obtained fuzzy model retains the acceptable performances of the original SVR solutions, and at the same time possesses high transparency. This enables a good compromise between the interpretability and accuracy of the fuzzy model.
Constructing interpretable kernels: Besides Gaussian kernel functions such as Eq. (4.61), there are some other common forms of membership functions:
The triangle membership function:
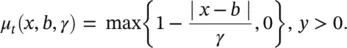
The generalized bell‐shaped membership function:
Читать дальше

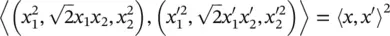
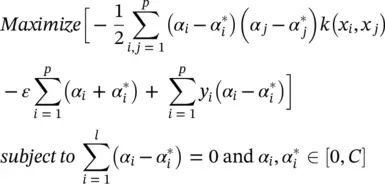
 and
and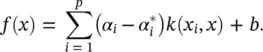
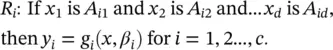
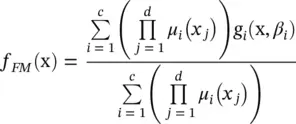
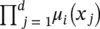 is the antecedent firing strength, and μ i( x j) is the membership of x jin the fuzzy set A i1. By the generalization of Eqs. (4.46)and (4.56), SVR is formulated as minimization of the following functional:
is the antecedent firing strength, and μ i( x j) is the membership of x jin the fuzzy set A i1. By the generalization of Eqs. (4.46)and (4.56), SVR is formulated as minimization of the following functional: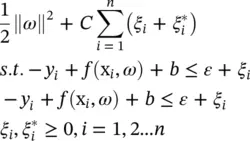
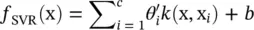
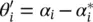 are subjected to constraints 0 ≤ α i,
are subjected to constraints 0 ≤ α i, 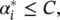 c is the number of support vectors, and the kernel k (x, x i) = 〈 Φ (x), Φ (x i)〉 is an inner product of the images in the feature space. The model given by Eq. (4.60)is referred to as the SVR model.
c is the number of support vectors, and the kernel k (x, x i) = 〈 Φ (x), Φ (x i)〉 is an inner product of the images in the feature space. The model given by Eq. (4.60)is referred to as the SVR model.