Savo G. Glisic - Artificial Intelligence and Quantum Computing for Advanced Wireless Networks

Table 3.3 Variables, for the derivation of gradient with ϕ ↔ φ .

	Alias	Size and Meaning
X	x l	H l W l× D l, the input tensor
F	f, w l	HW D l× D , D kernels, each H × W and D lchannels
Y	y, x l+1	H l + 1 W l + 1× D l + 1, the output, D l + 1= D
ϕ ( x l)		H l + 1 W l + 1× HW D l, the im2rowexpansion of x l
M		H l + 1 W l + 1 HW D l× H l W l D l, the indictor matrix for ϕ ( x l)
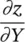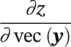		H l + 1 W l + 1× D l + 1, gradient for y
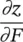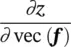		HW D l× D , gradient to update the convolution kernels
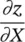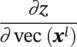		H l W l× D l, gradient for x l, useful for back propagation

From the chain rule, it is easy to compute ∂z /∂vec( F ) as

(3.91)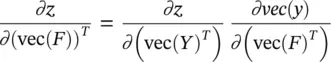

The first term on the right in Eq. (3.91)is already computed in the ( l + 1)‐th layer as ∂z / ∂ (vec( x l + 1)) T. Based on Eq. (3.89), we have

(3.92)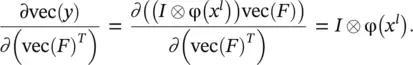

We have used the fact that ∂Xa T/ ∂a = X or ∂Xa / ∂a T= X so long as the matrix multiplications are well defined. This equation leads to

(3.93)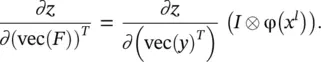

Taking the transpose, we get

(3.94)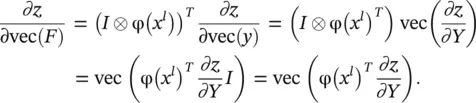

Both Eqs. (3.87)and (3.88)are used in the above derivation giving ∂z / ∂F = φ( x l) T ∂z / ∂Y , which is a simple rule to update the parameters in the l −th layer: the gradient with respect to the convolution parameters is the product between φ( x l) T(the im2col expansion) and ∂z / ∂Y (the supervision signal transferred from the ( l + 1)‐th layer).

Function φ( x l) has dimension H l + 1 W l + 1 HW D l. From the above, we know that its elements are indexed by a pair p , q . So far, from Eq. (3.84)we know: (i) from q we can determine d l, the channel of the convolution kernel that is used; and we can also determine i and j , the spatial offsets inside the kernel; (ii) from p we can determine i l + 1and j l + 1, the spatial offsets inside the convolved result x l + 1; and (iii) the spatial offsets in the input x lcan be determined as i l= i l + 1+ i and j l= j l + 1+ j . In other words, the mapping m : ( p , q ) → ( i l, j l, d l) is one to one, and thus is a valid function. The inverse mapping, however, is one to many (and thus not a valid function). If we use m −1to represent the inverse mapping, we know that m −1( i l, j l, d l) is a set S , where each ( p , q ) ∈ S satisfies m ( p , q ) = ( i l, j l, d l). Now we take a look at φ( x l) from a different perspective.

The question: What information is required in order to fully specify this function? It is obvious that the following three types of information are needed (and only those). The answer : For every element of φ( x l), we need to know

(A) Which region does it belong to, or what is the value of (0 ≤ p < H l + 1 W l + 1)?

(B) Which element is it inside the region (or equivalently inside the convolution kernel); that is, what is the value of q (0 ≤ q < HWDl )? The above two types of information determine a location ( p , q ) inside φ( x l). The only missing information is (C) What is the value in that position, that is, [φ( x l)] pq ?

Since every element in φ( x l) is a verbatim copy of one element from x l, we can reformulate question (C) into a different but equivalent one:

(C.1) Where is the value of a given [φ( x l)] pq copied from? Or, what is its original location inside x l, that is, an index u that satisfies 0 ≤ u < H l W l D l? (C.2) The entire x l.

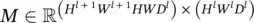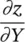
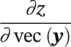
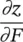
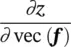
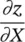
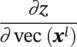
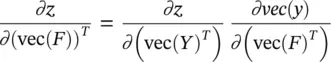
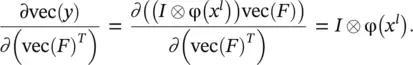
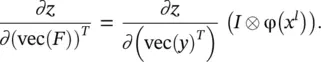
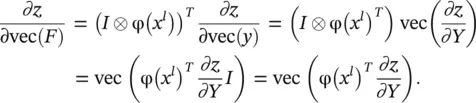
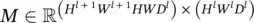It is easy to see that the collective information in [A, B, C.1] (for the entire range of p , q , and u , and (C.2) ( x l) contains exactly the same amount of information as φ( x l). Since 0 ≤ p < H l + 1 W l + 1, 0 ≤ q < HW D l, and 0 ≤ u < H l W l D l, we can use a a matrix to encode the information in [A, B, C.1]. One row index of this matrix corresponds to one location inside φ( x l) (a( p , q ) pair). One row of M has H l W l D lelements, and each element can be indexed by ( i l, j l, d l). Thus, each element in this matrix is indexed by a 5‐tuple: ( p , q , i l, j l, d l).