Savo G. Glisic - Artificial Intelligence and Quantum Computing for Advanced Wireless Networks

It is easy to see that z is a function of x in a chain‐like argument: a function maps x to y , and another function maps y to z . The chain rule can be used to compute ∂z / ∂x Tas

(3.78)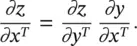

A CoNN usually takes an order‐3 tensor as its input, for example, an image with H rows, W columns, and three channels (R, G, B color channels). Higher‐order tensor inputs, however, can be handled by CoNN in a similar fashion. The input then goes through a series of processing steps. A processing step is usually called a layer, which could be a convolution layer, a pooling layer, a normalization layer, a fully connected layer, a loss layer , etc. We will introduce the details of these layers later.

For now, let us give an abstract description of the CNN structure first. Layer‐by‐layer operation in a forward pass of a CoNN can be formally represented as x 1→ w 1→ x 2→ ⋯ → x L − 1→ w L − 1→ x L→ w L→ z . This will be referred to as the operation chain . The input is x 1, usually an image (an order‐3 tensor). It undergoes the processing in the first layer, which is the first box. We denote the parameters involved in the first layer’s processing collectively as a tensor w 1. The output of the first layer is x 2, which also acts as the input to the second‐layer processing. This processing continues until all layers in the CoNN have been processed, upon which x Lis outputted.

An additional layer, however, is added for backward error propagation, a method that learns good parameter values in the CoNN. Let us suppose the problem at hand is an image classification problem with C classes. A commonly used strategy is to output x Las a C −dimensional vector, whose i ‐th entry encodes the prediction (the posterior probability of x 1comes from the i ‐th class). To make x La probability mass function, we can set the processing in the ( L − 1)‐th layer as a softmax transformation of x L − 1. In the other applications, the output x Lmay have other forms and interpretations.

The last layer is a loss layer. Let us suppose t is the corresponding target (ground truth) value for the input x 1; then a cost or loss function can be used to measure the discrepancy between the CoNN prediction x Land the target t . For example, a simple loss function could be z = ‖ t − x L‖ 2/2, although more complex loss functions are usually used. This squared ℓ 2loss can be used in a regression problem. In a classification problem, the cross‐entropy loss is often used. The ground truth in a classification problem is a categorical variable t . We first convert the categorical variable t to a C −dimensional vector . Now both t and x Lare probability mass functions, and the cross‐entropy loss measures the distance between them. Hence, we can minimize the cross‐entropy. The operation chain explicitly models the loss function as a loss layer whose processing is modeled as a box with parameters w L. Note that some layers may not have any parameters; that is, w imay be empty for some i . The softmax layer is one such example.

The forward run: If all the parameters of a CoNN model w 1, … , w L − 1have been learned, then we are ready to use this model for prediction, which only involves running the CNN model forward, that is, in the direction of the arrows in the operational chain. Starting from the input x 1, we make it pass the processing of the first layer (the box with parameters w 1), and get x 2. In turn, x 2is passed into the second layer, and so on. Finally, we achieve x L∈ ℝ C, which estimates the posterior probabilities of x 1belonging to the C categories. We can output the CNN prediction as arg max i .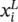

SGD: As before in this chapter, the parameters of a CoNN model are optimized to minimize the loss z ; that is, we want the prediction of a CoNN model to match the ground‐truth labels. Let us suppose one training example x 1is given for training such parameters. The training process involves running the CoNN network in both directions. We first run the network in the forward pass to get x Lto achieve a prediction using the current CoNN parameters. Instead of outputting a prediction, we need to compare the prediction with the target t corresponding to x 1, that is, continue running the forward pass until the last loss layer. Finally, we achieve a loss z . The loss z is then a supervision signal, guiding how the parameters of the model should be modified (updated). And the SGD method of modifying the parameters is w i← w i− η∂z / ∂w i. Here, the ←sign implicitly indicates that the parameters w i(of the i ‐layer) are updated from time t to t + 1. If a time index t is explicitly used, this equation will look like ( w i) t + 1= ( w i) t− η∂z / ∂ ( w i) t.

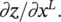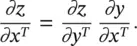
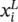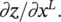Error backpropagation : As before, the last layer’s partial derivatives are easy to compute. Because x Lis connected to z directly under the control of parameters w L, it is easy to compute ∂z / ∂w L.This step is only needed when w Lis not empty. Similarly, it is also easy to compute If the squared ℓ 2loss is used, we have an empty ∂z / ∂w Land ∂z / ∂w L= x L− t . For every layer i , we compute two sets of gradients: the partial derivatives of z with respect to the parameters w iand that layer’s input x i. The term ∂z / ∂w ican be used to update the current ( i ‐th) layer’s parameters, while ∂z / ∂x ican be used to update parameters backward, for example, to the ( i − 1)‐th layer. An intuitive explanation is that x iis the output of the ( i − 1)‐th layer and ∂z / ∂x iis how x ishould be changed to reduce the loss function. Hence, we could view ∂z / ∂x ias the part of the “error” supervision information propagated from z backward until the current layer, in a layer‐by‐layer fashion. Thus, we can continue the backpropagation process and use ∂z / ∂x ito propagate the errors backward to the ( i − 1)‐th layer. This layer‐by‐layer backward updating procedure makes learning a CoNN much easier. When we are updating the i ‐th layer, the backpropagation process for the ( i + 1)‐th layer must have been completed. That is, we must already have computed the terms ∂z / ∂w i + 1and ∂z / ∂x i + 1. Both are stored in memory and ready for use.Now our task is to compute ∂z / ∂w iand ∂z / ∂x i. Using the chain rule, we have